花粉算法(Flower Pollination Algorithm, FPA)是英国剑桥大学学者Yang于2012年提出来的模拟花朵授粉的一种新型元启发式智能算法[1-2].该算法在实现的过程中需要调节的参数比较少, 能够将全局搜索与局部搜索相互转换, 还加入了随机搜索机制, 使得算法具有良好的寻优性能, 因此花粉算法在函数优化[3]、目标跟踪[4]、组合优化[5-6]、生产调度[7]、文本聚类[8-9]、电力系统[10]等众多领域中得到广泛的应用.
花粉算法和其他智能算法同样存在易陷入局部最优和收敛速度慢等缺点, 而且在全局搜索能力、鲁棒性等方面仍然存在不足.为此, 众多国内外学者对基本花粉算法存在的缺陷进行改进, 井福荣等[11]提出了一种使用反向学习策略改进的花粉算法, 该算法在运行的过程中利用反向学习策略对当前种群进行反向变换, 并将反向变换的种群和当前种群进行竞争, 再选择较优秀的个体; Lu等[12]提出了基于量子行为的花粉算法, 该算法通过引入量子行为的叠加、相干和并行等特性, 利用波函数表示花粉个体的位置, 用δ势阱束缚花粉个体, 从而使其以一定的概率密度在可行空间的任何区域进行搜索, 避免算法在很大程度上陷入局部最优; Nguyen[13]提出了一种交流策略的并行花粉算法, 该算法将花粉分为若干个组, 独立进行迭代, 通过通讯策略, 各组进行花粉个体交换, 在很大程度上避免陷入局部最优; 肖辉辉等[14]提出了基于单纯形法和自适应步长的花粉算法, 该算法利用单纯形法提高局部搜索能力, 通过自适应步长提高全局收敛能力.上述改进方法虽然在一定程度上提高了算法的性能, 但是在收敛速度、全局寻优方面以及鲁棒性方面仍需要一定的改进.
本文针对花粉算法存在的缺陷, 将协作搜索策略加入到FPA中, 提出一种协作搜索的花粉算法(COFPA), 将种群中的所有个体通过自身信息的交流协作, 对每次迭代的最优解进行逐维比较, 逐维更新最优解, 加快算法收敛速度, 增强算法的全局寻优性能.通过对基准测试函数的测试, 结果表明, 该算法收敛速度有了较大的提升, 同时也能够避免陷入局部最优并有较好的鲁棒性.
1 算法原理花粉算法是模拟自然界中显花植物花朵传粉过程, 为了更好地模拟自花授粉和交叉授粉过程, 作出以下假设[1]:
(1) 生物的异花授粉是携带花粉的传粉者通过Lévy飞行进行全局授粉的过程;
(2) 非生物自花授粉可以看做是局部授粉的过程;
(3) 花的常性可以被认为是繁衍概率, 繁衍概率与参与的两朵花的相似性成比例关系;
(4) 转换概率p∈[0, 1], 控制全局授粉和局部授粉之间的转换.受距离及其他因素的影响, 整个授粉过程更倾向于自花授粉.
在FPA算法的初始阶段, 随机产生一个包含N个个体的种群P(t)={Xit}, Xit=[Xi, 1t, Xi, 2t, …, Xi, jt, …, Xi, Dt](i=1, 2, …, n, j=1, 2, …, D), 其中D是优化问题的维数, t为当前的迭代次数, N为种群的大小, 代表解的多样性.
交叉授粉是传粉者通过Lévy飞行进行的全局授粉过程, 即
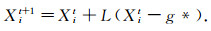
|
(1) |
其中, Xit是表示第t次迭代时花粉i的位置, g*表示的是当前群体的最优解, 参数L为步长, 服从Lévy分布.
自花授粉即局部授粉过程为
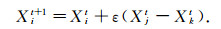
|
(2) |
其中变异因子ε是[0, 1]上服从均匀分布的随机数, Xjt, Xkt是表示同一类植物的不同花的花粉.
优化算法的最终目标都是求得一个d维的最优向量.在算法的每次迭代结束, 都会将某个个体当做全局最优解.在迭代过程中, 即使某一个体的某一分量找到了该维的最优解, 但是个体的适应度值是根据整个向量来确定的, 如果该个体不是最优解, 那么最优分量也就会舍去.因此为了保留最优分量, 本文提出了一种基于协作搜索策略的花粉算法(COFPA).该算法通过种群间的所有个体相互交流协作, 对每次迭代的全局最优值运用控制变量法逐维更新当前全局最优解, 最终通过每个花粉个体的协作找到向量中每一个分量的最优值.
2 基于协作搜索的花粉算法在COFPA中, 最优位置为gbest, 记作gb, 其中f(x)为目标函数.分别用每个花粉个体的第j(1, 2, …, D)个分量来代替gb中相应的元素变成newbest, 记作nb, 代入目标函数计算适应度值, 如果f(nb)优于f(gb), 则用nb代替gb, 从而找到第j维的最优值.将算法改进后能够在很大程度上加快花粉算法的收敛速度.
COFPA步骤如下:
(1) 初始化算法的基本参数.设置种群N, 转换概率p, 最大迭代次数N-iter.
(2) 随机初始化个体的位置, 计算每个个体的适应度值, 并求解当前的全局最优值和最优解.
(3) 如果转换概率p < rand条件成立, 按式(1)对解进行更新, 并进行越界处理.
(4) 如果转换概率p>rand条件成立, 按式(2)对解进行更新, 并进行越界处理.
(5) 步骤(3)或者(4)得到新解对应的适应度值, 若新解的适应度值优, 则用新解和新解对应的适应度值分别替换当前解和最优值.否则, 保留当前解和当前适应度值.
(6) 如果新解对应的适应度值比全局最优值优, 则更新全局最优解和全局最优值.
(7) 进行协作搜索策略, 逐维比较更新全局最优解.
(8) 判断结束条件, 若满足, 退出程序并输出最优值及最优解, 否则, 转步骤(3).
改进后的算法, 在每次迭代后, 就会对全局最优值进行进一步的更新, 很大程度上优化全局最优解, 理论上不仅能够避免花粉算法陷入局部最优, 同时能够提高算法的收敛速度.
3 数值试验 3.1 参数设置及测试函数测试环境为:操作系统为Windows 7, CPU为Intel Core i5-3210 M, 主频为2.5 GHz, 内存为4 GB, 编程语言为MATLAB 2015b.在COFPA算法中, 设定种群规模N=20, 转换概率p=0.8.
为了验证COFPA算法的性能, 选取8个具有代表性的函数作为本文的测试函数[15].并与标准的FPA算法以及改进的FA-FPA算法进行比较[16].本文测试函数如下:
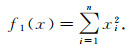
|
该函数在xi=0(xi∈[-5.12, 5.12], i=1, 2, …, n)处取得全局min(f1(x))=0.
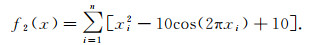
|
该函数在xi=0(xi∈[-5.12, 5.12], i=1, 2, …, n)处取得全局min(f2(x))=0.
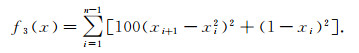
|
该函数在xi=1(xi∈[-30, 30], i=1, 2, …, n-1)处取得全局min(f3(x))=0.
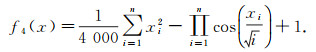
|
该函数在xi=0(xi∈[-600, 600], i=1, 2, …, n)处取得全局min(f4(x))=0.
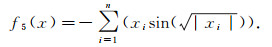
|
该函数xi=420.968 7(xi∈[-500, 500], i=1, 2, …, n)取得min(f5(x))=-412.982 9n.
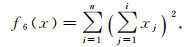
|
该函数在xi=0(xi∈[-100, 100], i=1, 2, …, n)处取得全局min(f6(x))=0.
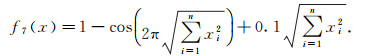
|
该函数在xi=0(xi∈[-100, 100], i=1, 2, …, n)处取得全局min(f7(x))=0.
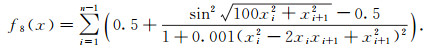
|
该函数在xi=0(xi∈[-100, 100], i=1, 2, …, n-1)处取得全局min(f8(x))=0.
3.2 结果及分析. 3.2.1 固定迭代次数分析在测试中, 为了克服实验偶然性带来的误差, 针对每个测试函数, 分别利用FA算法、FPA算法以及文献[16]中提出的FA-FPA算法, 每种算法独立运行30次, 并统计其结果, 如表 1.
| 函数 | 算法 | 最优值 | 平均值 | 最差值 | 方差 |
| f1 | FPA | 1.138 2×10-7 | 1.644 21×10-5 | 8.342 4×10-5 | 7.619 1×10-10 |
| FA-FPA | 6.823 1×10-8 | 3.873 7×10-7 | 1.432 8×10-6 | 6.427 5×10-14 | |
| COFPA | 2.969 9×10-9 | 4.175 5×10-8 | 2.265 2×10-7 | 3.549 8×10-15 | |
| f2 | FPA | 0.037 6 | 0.299 8 | 0.994 9 | 0.214 7 |
| FA-FPA | 4.796 4×10-4 | 2.784 8×10-3 | 7.489 3×10-2 | 4.376 2×10-4 | |
| COFPA | 0 | 1.073 8×10-8 | 1.637 1×10-7 | 1.135 1×10-7 | |
| f3 | FPA | 0 | 0 | 0 | 0 |
| FA-FPA | 0 | 0 | 0 | 0 | |
| COFPA | 0 | 0 | 0 | 0 | |
| f4 | FPA | 1.006 3×10-4 | 9.278 9×10-3 | 2.957 9×10-2 | 2.869 5×10-5 |
| FA-FPA | 3.342 5×10-3 | 5.433 8×10-2 | 0.387 4 | 3.397 8×10-4 | |
| COFPA | 0 | 3.543 3×10-4 | 4.635 2×10-3 | 6.446 8×10-7 | |
| f5 | FPA | -2 094.914 4 | -2 031.747 3 | -1 976.476 1 | 3 611.711 9 |
| FA-FPA | -2 094.914 4 | -2 048.835 4 | 2 019.351 2 | 2 479.364 7 | |
| COFPA | -2 094.914 4 | -2 094.914 4 | -2 094.914 4 | 0 | |
| f6 | FPA | 1.243 7×10-39 | 1.353 8×10-28 | 2.014 2×10-27 | 1.915 82×10-55 |
| FA-FPA | 0 | 0 | 0 | 0 | |
| COFPA | 0 | 0 | 0 | 0 | |
| f7 | FPA | 0.199 8 | 0.479 8 | 1.099 9 | 0.055 92 |
| FA-FPA | 0.107 3 | 0.428 7 | 0.932 6 | 0.049 73 | |
| COFPA | 0.098 73 | 0.276 5 | 0.599 8 | 0.012 93 | |
| f8 | FPA | 3.054 1×10-3 | 8.5484×10-2 | 0.363 6 | 0.010 39 |
| FA-FPA | 1.734 2×10-3 | 3.286 6×10-2 | 0.923 1 | 0.138 52 | |
| COFPA | 5.382 7×10-7 | 6.527 4×10-3 | 1.775 1×10-2 | 3.502 1×10-5 |
在统计结果中, 最优值反应解的质量, 平均值显示了解能达到的精度, 方差反映了算法的鲁棒性和稳定性.从表 1的实验结果可以看出, 相对于FPA以及FA-FPA算法来说, 在函数f1~f8, COFPA算法在最优值、平均值、最差值以及方差都要优于标准的FPA算法和FA-FPA算法.对其中3个测试函数来说, COFPA算法总能找到得到的最优值, 而FPA算法和FA-FPA算法找不到.FPA算法和FA-FPA算法在测试函数中容易陷入局部最优, 而COFPA算法能够跳出局部最极小, 每次实验总能达到理论最优.COFPA算法的实验结果方差都优于FPA算法和花粉算法, 说明改进的COFPA算法的鲁棒性和稳定性都优于其他算法.COFPA算法在总体上比FPA算法和FA-FPA算法的性能有较大幅度的提高.
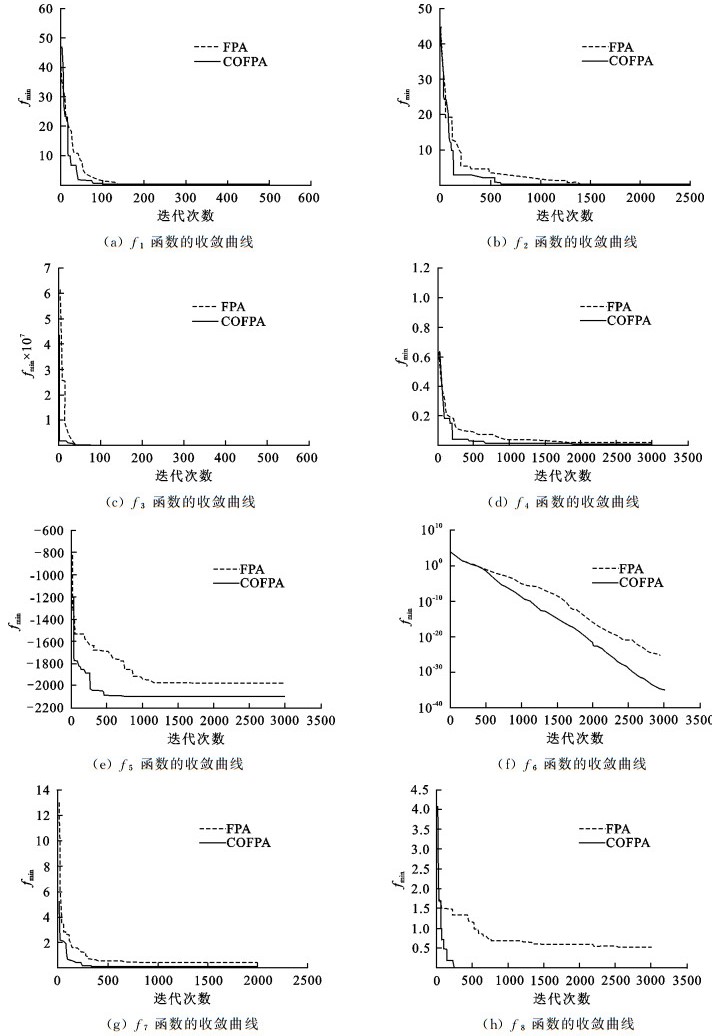
为了直观地比较COFPA算法和标准FPA算法的寻优精度和收敛速度, 画出FPA算法和COFPA算法在测试函数上的收敛曲线图, 如图 1所示.
|
| 图 1 FPA和COFPA收敛曲线比较 Fig.1 Comparison of convergence curves of FPA and COFPA |
从图 1的收敛曲线很容易看出, 在测试函数中, 相对于FPA算法, COFPA算法有较快的收敛速度.对测试函数f5, f7, f8来说, COFPA算法不仅具有更好收敛精度, 而且很容易达到全局最优, 然而FPA算法容易陷入局部极小值.对测试函数f2, f4, f6来说, COFPA算法在迭代后期的收敛速度明显优于FPA算法.总体上, COFPA算法比FPA算法在性能上有了显著的提高.
3.2.2 算法的T检验在实验中, 两种算法在8个标准测试函数上均独立运行30次, 因而在每个标准测试函数上, 每个算法都有30个样本.采用T检验法比较FPA和COFPA的性能[17].该T检验使用显著水平为0.05的双尾检验, 其结果如表 2.其中“+”表示COFPA在对应函数计算结果的显著性优于FPA, “=”表示的是COFPA在对应函数上的性能与FPA是相等的.
| 函数 | 显著性 | 函数 | 显著性 |
| f1 | + | f5 | + |
| f2 | + | f6 | = |
| f3 | = | f7 | + |
| f4 | + | f8 | + |
从表 2中可以看出, COFPA对于函数f3以及f6的显著性与FPA相同; 对于函数f1, f2, f4, f5, f7, f8来说, COFPA显著性优于FPA.从统计学的角度来看, COFPA在测试函数上的显著性优于FPA.
4 结束语FPA算法是一种新型的元启发式群智能算法, 已经被广泛应用到解决实际生活问题中.由于FPA算法与现有的群智能算法一样, 存在收敛精度低、收敛速度慢、易陷入局部最优等缺陷.本文提出了一种基于协作搜索策略的花粉算法, 实验结果表明, 改进后的COFPA算法不仅容易跳出局部极小值, 而且还具有较快的收敛速度和寻优精度, 极大地提高了算法的性能.
然而, COFPA算法也有其自身的局限性, 对于有些优化问题, COFPA算法的改进效果并不是太明显.FPA算法的理论知识也不是很完善.在今后的研究工作中, 不仅完善FPA算法的理论知识有一定的价值, 而且应用领域也需要进一步的推广.
| [1] | YANG X.Flower pollination algorithm for global optimization[C]//Proceedings of the 11th International Conference on the Unconventional Computation and Natural Computation, LNCS 7445.Berlin:Springer-Verlag, 2012:240-249. |
| [2] | YANG X S. Nature-inspired metaheuristic algorithm[M]. UK: Luniver Press, 2008: 81-96. |
| [3] | YANG X S, KARAMANOGLU M, HE X. Multi-objective flower pollination algorithm for optimization[J]. International Conference on Computations Science, 2013, 18: 861-868 |
| [4] | GAO M L, ZANG Y R, JIN S.Visual tracking based on flower pollination algorithm[C]//Control Conference.IEEE, 2016:3866-3868. |
| [5] |
冯翔, 张进文, 虞慧群. 仿生蚊子追踪算法[J].
计算机学报, 2014, 37(8): 1794-1808 FENG X, ZHANG J W, YU H Q. Mosquito host-seeking algorithm for TSP problem[J]. Chinese Journal of Computers, 2014, 37(8): 1794-1808 |
| [6] |
张迷, 贺兴时. 多目标优化问题的花授粉算法改进[J].
西安工程大学学报, 2016, 30(3): 393-399 ZHANG M, HE X S. An improvement of flower pollination algorithm in multi-objective optimization[J]. Journal ofXi'anPolytechnic University, 2016, 30(3): 393-399 |
| [7] |
马雪丽, 曹德弼, 刘晓冰. 面向柔性工艺的作业车间调度问题混合遗传算法[J].
计算机应用研究, 2014, 31(5): 1353-1357 MA X L, CAO D B, LIU X B. Hybrid generic algorithm solving flexible process Job-Shop scheduling problem[J]. Application Research of Computers, 2014, 31(5): 1353-1357 |
| [8] | KAUR M, KAUR N. Text clustering using PBO algorithm for analysis and optimization[J]. International Journal of Current Engineering and Technology, 2014, 4(6): 3876-3878 |
| [9] |
张姣, 王晓东, 薛红. 基于花粉算法的K均值聚类算法[J].
织高校基础科学学报, 2016, 29(4): 563-569 ZHANG J, WANG X D, XUE H. K-means clustering algorithm based on flower pollination algorithm[J]. Basic Sciences Journal of Textile Universities, 2016, 29(4): 563-569 |
| [10] | CHATTOPADHYAY S, BANERJEE S.Optimum power allocation of parallel concatenated convolution turbo code using flower pollination algorithm[C]//International Conference on Control, Instrumentation, Energy & Communication (CIEC).International Conference on Control, 2016:516-520. |
| [11] |
井福荣, 郭肇禄, 罗兰会. 一种使用反向学习策略的改进花授粉算法[J].
江西理工大学学报, 2015, 36(3): 101-106 JING F R, GUO Z L, LUO L H. A flower pollination algorithm based on reverse learning strategy[J]. Journal of Jiangxi University of Science and Technology, 2015, 36(3): 101-106 |
| [12] | LU K Z, LI H B.Quantum-behaved flower pollination algorithm[C]//2015 14th International Symposium on Distributed Computing and Applications for Engineering and Science (DCABES).Guiyang, 2015:66-69. |
| [13] | NGUYEN T T, SHIEH C S, HORNG M F.Parallelized flower pollination algorithm with a communication strategy[C]//Knowledge and Systems Engineering.IEEE, 2015:103-107. |
| [14] |
肖辉辉. 基于单纯形法和自适应步长的花朵授粉算法[J].
计算机工程与科学, 2016, 38(10): 2126-2133 XIAO H H. A flower pollination algorithm based on simplex method and self-adaptive step[J]. Computer Engineering & Science, 2016, 38(10): 2126-2133 DOI:10.3969/j.issn.1007-130X.2016.10.025 |
| [15] | JAMIL, YANG X S. A literature survey of benchmark function for global optimization problems[J]. Int J Mathematical Modeling and Numerical Optimization, 2013(4): 150-194 |
| [16] |
卞京红, 贺兴时, 杨新社. 基于萤火虫算法的自适应花授粉优化算法[J].
计算机工程与应用, 2016, 52(21): 162-167 BIAN J H, HE X S, YANG X S. Hybrid algorithm of firefly algorithm and self-adaptive flower pollination algorithm[J]. Computer Engineering and Applications, 2016, 52(21): 162-167 DOI:10.3778/j.issn.1002-8331.1603-0412 |
| [17] |
乔现伟, 贺兴时, 杨新社. 基于混沌的花粉算法[J].
纺织高校基础科学学报, 2015, 28(3): 85-100 QIAO X W, HE X S, YANG X S. Chaos-based flower algorithm[J]. Basic Sciences Journal of Textile Universities, 2015, 28(3): 85-100 |



