Orlicz[1]在研究积分方程时, 引入了一个比Lp空间更一般的函数空间, 即Orlicz空间. Orlicz空间理论对偏微分方程、泛函分析、非线性分析和积分方程等研究起了很大作用.王立河等[2]、贾慧莲等[3]和Byun等[4]利用紧性方法, 区域分解方法研究了椭圆方程和抛物方程相应的Orlicz估计[5].特别地, 文献[2]在Young函数φ满足增长性条件Δ2∩∇2下把Possion方程
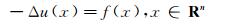
|
的Lp估计[6]推广到Orlicz估计.另外, 证明了φ满足的增长性条件Δ2∩∇2是最优的, 其中Rn (n≥2)是欧氏空间.
海森堡群[7-8]是一类非平凡的次黎曼流形, 其几何结构与欧氏空间有本质区别.例如, 海森堡群上的基向量场是非交换的.本文研究了海森堡群Hn上Kohn-Laplace方程
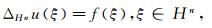
|
(1) |
其中ΔHn为Kohn-Laplace算子, 其Lp估计见文献[9-10].在Young函数φ满足增长性条件Δ2∩∇2下, 文献[11]得到了算子ΔHn的Orlicz估计.文献[12-13]分别研究了分层Lie群上非散度椭圆方程和Schrdinger方程的Orlicz估计.文献[14-16]在增长性条件Δ2∩∇2下, 建立群上二阶偏微分方程的Orlicz估计.目前, 还未见文献证明海森堡群上Kohn-Laplace方程的Orlicz估计中的增长性条件Δ2∩∇2是最优的.
为了将文献[2]中的定理1.5的必要性推广到海森堡群上, 即证明增长性条件Δ2∩∇2是最优的.首先通过估计海森堡群上Kohn-Laplace算子在原点的基本解的二阶导数, 证明Young函数φ满足全局∇2条件, 然后利用切断函数构造两个常数, 并结合φ∈∇2得到φ∈Δ2.
1 预备知识和主要结果 1.1 海森堡群令ξ=(z, t)=(x, y, t)∈ R2n+1, 其中x=(x1, x2, …, xn)∈ Rn, y=(y1, y2, …, yn)∈ Rn, n∈ N且显然有zi=xi, zn+i=yi, i=1, 2, …, n. 〈x, y〉表示Rn中通常的内积, 即
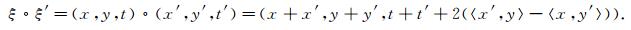
|
Hn上的向量场
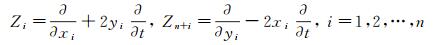
|
及其交换子可以张成整个Lie代数, 即Z1, Z2, …, Z2n满足Hörmander有限秩条件[17]. Kohn-Laplace算子ΔHn定义为
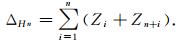
|
(2) |
Hn的一个重要的自同构群是由海森堡伸缩δλ(z, t)=(λz, λ2t)给出的, 其中λ>0. Hn的齐次维数为Q=2n+2.令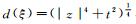
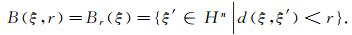
|
记函数类Φ={φ:[0, +∞)→[0, +∞)|φ是单调递增的凸函数}.
定义1[18] 如果函数φ∈Φ, 且
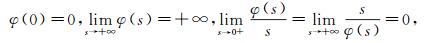
|
则称φ为Young函数.
定义2[18] 一个Young函数φ称为满足全局Δ2条件, 记为φ∈Δ2, 如果存在常数K>0使得对任意的s>0, 有
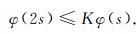
|
由文献[2]可知, 若φ∈Δ2, 对任意的1≤θ2 < ∞, 有

|
(3) |
其中α1=log2K.
定义3[18] 一个Young函数φ称为满足全局∇2条件, 记为φ∈∇2, 如果存在常数a>1使得∀s>0, 有
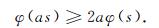
|
由文献[2]可知, 若φ∈∇2, ∀0 < θ1≤1, 有
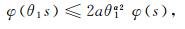
|
(4) |
其中α2=loga2+1.
定义4[18] 设φ是一个Young函数, 海森堡群Hn上的Orlicz类Kφ(Hn)是由满足

|
的可测函数g:Hn→ R构成的集合.Hn上的Orlicz空间Lφ(Hn)是Orlicz类Kφ(Hn)的线性闭包.在Orlicz空间Lφ(Hn)中, 模定义为
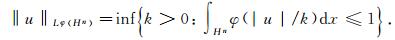
|
记
定理1 设Young函数φ∈Φ, 如果对满足方程(1)的(u, f)∈C∞(Hn)×C0∞(Hn)且|Z2u|∈Lφ(Hn), 有下式成立:
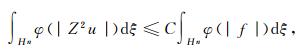
|
(5) |
则φ∈Δ2∩∇2, 其中正常数C与u和f无关.
注1 文献[11]在φ∈Δ2∩∇2条件下, 得到了估计式(5).
2 定理1的证明以下分两步来证明定理1.
第一步 证明φ满足全局∇2条件.
令fs(ξ)=sη(ξ), 其中参数s>0, η(ξ)∈C0∞ (Hn)是切断函数, 且
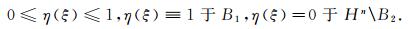
|
(6) |
由文献[15]可知, ΔHn在原点的基本解为
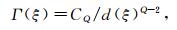
|
(7) |
其中Q是Hn的齐次维数, CQ是仅依赖于Q的正常数.则由文献[11]可知

|
(8) |
满足方程(1). ξ′=(x′, y′, t′)的逆元ξ′-1=(-x′, -y′, -t′), 利用群运算法则得
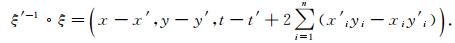
|
然后由距离d的定义得
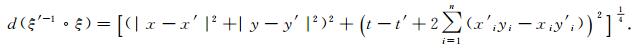
|
(9) |
结合式(6)~(8)得

|
(10) |
由式(5)~(6)得
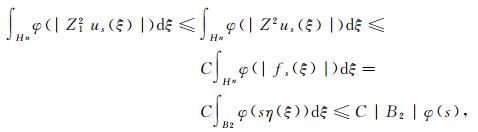
|
(11) |
其中|B2|表示Hn中半径为2的度量球的Haar测度, |B2|=CQ2Q, CQ是仅依赖于齐次维数Q的正常数.
下面估计Z12 us(ξ).利用式(10)得
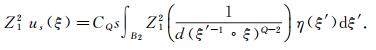
|
(12) |
首先计算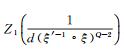
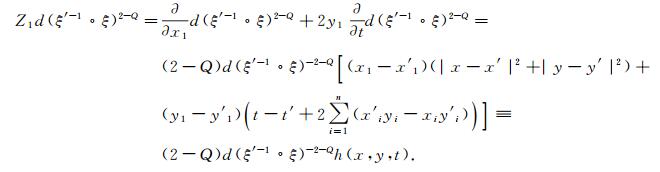
|
其中
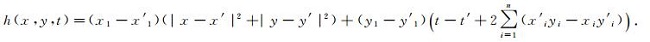
|
进一步得

|
(13) |
注意到
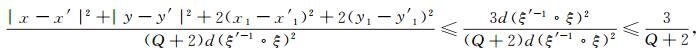
|
以及存在充分大的常数C0>9使得当|x1|>C0时, 有
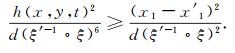
|
因此, 对|x1|>C0有
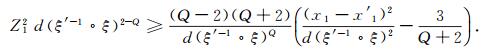
|
令

|
由文献[16]知d是Hn上的距离, 即
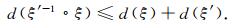
|
(14) |
对ξ∈Ω, ξ′∈B1, 有
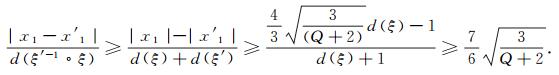
|
(15) |
对ξ∈Ω, ξ′∈B2\B1, 有

|
(16) |
所以, 对ξ∈Ω, 利用式(12)~(16), 得

|
(17) |
其中CQ是仅依赖于Q的正常数.
由式(11)和(17), 得
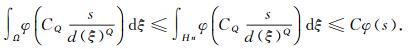
|
(18) |
由式(18)和极坐标变换得

|
令λ=CQsr-Q, 则dλ=-CQQsr-Q-1dr.由上式可知, ∀s>0, 有
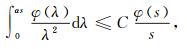
|
(19) |
其中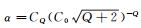
令s2≥s1>0, 0 < ε≤α/2.在式(19)中取s=s2, 由φ是增函数得
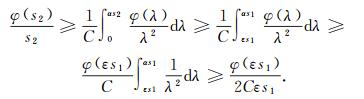
|
(20) |
在式(20)中取s2=λ, s1=εs, 并结合式(19)得
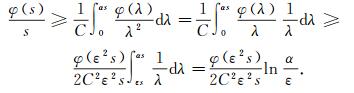
|
(21) |
令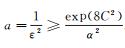
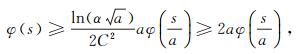
|
即φ∈∇2.
第二步 证明φ满足全局Δ2条件.
构造如下两个常数:
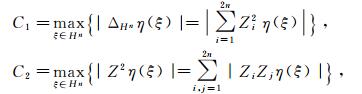
|
其中切断函数η(ξ)与式(6)相同.显然C1 < C2.令
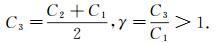
|
令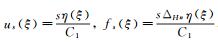
由第一步知φ∈∇2.则由式(4)~(5), 得
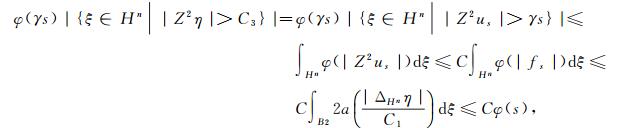
|
即φ(γs)≤φ(s), 从而φ∈Δ2.
综上所述, φ∈Δ2∩∇2, 即定理1得证.
| [1] | ORLICZ W. Üeber eine gewisse Klasse von Räumen vom Typus B[J]. Bulletin International de l'Academie Polonaise Série A, 1932(8): 207-220 |
| [2] | WANG L H, YAO F P, ZHOU S L, et al. Optimal regularity for the Poisson equation[J]. Proceedings of the American Mathematical Society, 2009, 137(6): 2037-2047 DOI:10.1090/S0002-9939-09-09805-0 |
| [3] | JIA H L, LI D S, WANG L H. Regularity theory in Orlicz spaces for elliptic equations in Reifenberg domains[J]. Journal of Mathematical Analysis and Applications, 2007, 334(2): 804-817 DOI:10.1016/j.jmaa.2006.12.081 |
| [4] | BYUN S S, LEE M. Weighted estimates for nondivergence parabolic equations in Orlicz spaces[J]. Journal of Functional Analysis, 2015, 269(8): 2530-2563 DOI:10.1016/j.jfa.2015.07.009 |
| [5] | ZHU M C, NIU P C, FENG X J. Orlicz regularity for non-divergence parabolic systems with partially VMO coefficients[J]. Mathematica Scandinavica, 2015, 116(1): 141-160 DOI:10.7146/math.scand.a-20455 |
| [6] | GILBARG D, TRUDINGER N S. Elliptic partial differential equations of second order[M]. Berlin: Springer-Verlag, 2001: 235-243. |
| [7] |
李俊兵, 魏娜. Heisenberg群上高阶退化椭圆方程解的Morrey正则性[J].
纺织高校基础科学学报, 2009, 22(4): 459-462 LI J B, WEI N. Morrey regularity of higher order degenerate elliptic equation on the Heisenberg group[J]. Basic Sciences Journal of Textile Universitise, 2009, 22(4): 459-462 |
| [8] |
王彦林, 赵宁波. Heisenberg群上一类半线性次椭圆方程解的有界性[J].
纺织高校基础科学学报, 2011, 24(4): 485-488 WANG Y L, ZHAO N B. solvbilivity theorem of half semilinear elliptic equations on Heisenberg group[J]. Sciences Journal of Textile Universities, 2011, 24(4): 485-488 |
| [9] | FOLLAND G B. Subelliptic estimates and function spaces on nilpotent Lie groups[J]. Arkiv för Matematik, 1975, 13(1): 161-207 |
| [10] | BRAMANTI M. An invitation to hypoelliptic operators and Hörmander's vector fields[M]. New York: Springer, 2014: 31-54. |
| [11] | FENG X J, NIU P C. Global Orlicz regularity for sub-Laplace equations on homogeneous groups[J]. Bulletin des Sciences Mathématiques, 2012, 136(6): 648-665 DOI:10.1016/j.bulsci.2012.01.003 |
| [12] | NIU P C, ZHU M C. Regularity in Orlicz spaces for nondivergence degenerate elliptic equations in Carnot groups[J]. Revista de la Real Academia de Ciencias Exactas Fisicas Y Naturales, Serie A, Matematicas, 2014, 108(2): 577-601 DOI:10.1007/s13398-013-0127-5 |
| [13] |
张克磊. Carnot群上Schrödinger方程解的全局Orlicz正则性[J].
纺织高校基础科学学报, 2015, 28(4): 440-446 ZHANG K L. Global Orlicz regularity for solutions of Schrödinger equations on Carnot groups[J]. Basic Sciences Journal of Textile Universities, 2015, 28(4): 440-446 |
| [14] | BONFIGLIOLI A, LANCONELLI E, UGUZZONI F. Stratified Lie groups and potential theory for their sub-Laplacians[M]. Berlin: Springer, 2007: 87-286. |
| [15] | FOLLAND G B. A fundamental solution for a subelliptic operator[J]. Bulletin of the American Mathematical Society, 1973, 79(2): 373-376 DOI:10.1090/S0002-9904-1973-13171-4 |
| [16] | CYGAN J. Wiener's test for the Brownian motion on the Heisenberg group[J]. Colloquium Mathematicae, 1978, 39(2): 367-373 DOI:10.4064/cm-39-2-367-373 |
| [17] | HÖRMANDER L. Hypoelliptic second order differential equations[J]. Acta Mathematica, 1967, 119(1): 147-171 |
| [18] | RAO M M, REN Z D. Applications of Orlicz spaces[M]. New York: Marcel Dekker Inc, 2000: 45-96. |


