肺结核是常见的一种呼吸道传染病.我国是结核病高发国家之一, 每年大约有13万人死于肺结核, 对于肺结核的预防和控制至关重要.疾病最有效的控制方法是对患者进行治疗和对易感者进行接种.目前治疗结核病主要是依靠化学药物杀灭体内的结核菌, 由于肺结核潜伏期长, 还有患者的服药依从性问题, 会引起治疗不及时或不彻底, 从而会不断传染周围人, 造成肺结核病的蔓延.除此以外, 对易感群体接种疫苗是避免感染结核病的行之有效的方法.我国规定新生儿出生都要进行卡介苗接种, 儿童、成人也会要求进行卡介苗的接种.
近年来有很多传染病模型的研究[1-2], 关于肺结核也有许多不同方面的研究[3-16].如文献[3]研究了不完全治疗对肺结核传播模型的动力学性态的影响;文献[4]分析了不完全治疗和新生儿接种的肺结核传播模型的全局动力学性态;文献[5-6]研究了一类具有快慢进程的肺结核模型的全局性态;文献[7]讨论了常数输入的肺结核模型的动力学性态;文献[8]考虑了一般发生率对疾病传播的影响;文献[9]研究了重复感染对模型动力学性态的影响.尽管这些文献考虑了新生儿接种对于肺结核病的影响[3, 5, 9-11], 但却很少有人考虑易感者接种对肺结核的影响.本文在文献[3-4]的基础上, 根据肺结核的传播特点, 考虑不完全治疗和对新生儿进行接种, 以及对易感者进行接种的更为实际的模型,并研究模型的动力学性态, 得到关于疾病灭绝的条件.
1 模型建立把总人口N分为五个仓室, 分别为S, L, I, T, V.其中S是易感者, 没有感染过肺结核病史; L是潜伏者, 表示个体被Mtb(结核杆菌)所感染, 但没有传染性; I是传染者, 表示个体被Mtb所感染, 且具有一定的传染性; T是治疗者, 表示正在接受治疗的个体; V是接种者, 表示通过接种而暂时获得免疫能力的个体(V中的人口数目远多于其他仓室的人口数目).建立如下的数学模型:

|
(1) |
式中:A表示总人口的常数输入率, p(0≤p≤1)表示新生儿的接种比例系数, b表示对易感者的接种比例系数, c表示被接种者的免疫丧失率系数(c>b>0), d表示自然死亡率系数, α1, α2分别表示个体在I、T中的因病死亡率系数, β表示传染率系数, σ(0 < σ < 1)表示个体经过接种后再次被感染率, γ表示染病者接受治疗的治疗率, q(0≤q < 1)表示染病者通过治疗到潜伏类的移出率, ε表示个体从潜伏者L到传染者I的转化率系数, k(0≤k≤1)表示个体接受治疗并治疗成功的比率, δ表示治疗者离开仓室T的转移率.
为方便计算, 令m1=b+d, m2=ε+d, m3=γ+d+α1, m4=δ+d+α2, m5=c+d.因此, 上式又可写为
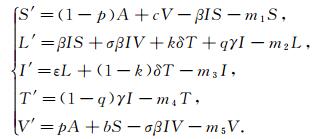
|
对于系统(1), 有(S+L+I+T+V)′=A-d(S+L+I+T+V)-α1T-α2T≤A-d(S+L+I+T+V), 即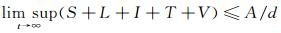
系统(1)有唯一的无病平衡点E0(S0, 0, 0, 0, V0), 其中

|
根据文献[17]中的定理2, 系统(1)基本再生数是

|
关于系统(1)的地方病平衡点E*(S*, L*, I*, T*, V*), 可以根据下面的方程得出
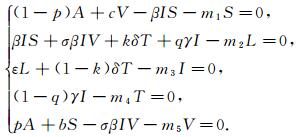
|
(2) |
根据上述方程的第一, 第三, 第四和第五个等式, 可以得到

|
(3) |
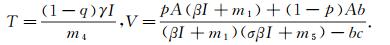
|
把式(3)代入式(2)中第二个等式则有

|
这里
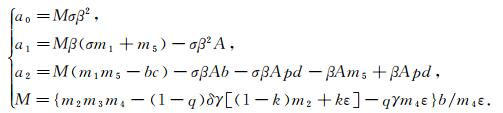
|
记Φ(I):=a0I2+a1I+a2, 当m2m3m4-(1-q)δγ[(1-k)m2+kε]-qγm4ε>0时, 可以证明M>0.那么∃a0>0, 当且仅当R0>1时有a2 < 0.因此, 当R0>1时, Φ(I)存在唯一的正根I*, 且I*∈(0, A/d), 有Φ(0)=a2 < 0.所以, 当R0>1时, 模型存在唯一的正平衡点E*(S*, L*, I*, T*, V*).为此, 可以得到下面的平衡点存在定理.
定理1 对于系统(1), 如果R0≤1, 则系统(1)有唯一的无病平衡点E0(S0, 0, 0, 0, V0); 如果R0>1, 则除了无病平衡点E0以外, 系统(1)还有正的平衡点E*(S*, L*, I*, T*, V*), 这里I*∈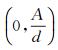
关于系统(1)平衡点的全局稳定性, 有以下的结论.
定理2 对于系统(1), 如果R0≤1, 则在集合Ω上无病平衡点E0是全局渐近稳定的.
证明 定义函数H1=εm4L+m2m4I+δ[kε+m2(1-k)]T, 则

|
定义Lyapunov函数

|
那么, W1沿着系统(1)的全导数是

|
这里

|
把F(S, V)看成一个关于S-S0的一元二次函数, 这时只要Δ < 0, 则有F(S, V) < 0.
由模型(1)可知S0, V0满足

|
将其代入Δ中, 有

|
因为p≤1, 所以F(S, V)≤0, 并且当且仅当S=S0, V=V0时有F(S, V)=0.同时注意到, 当R0≤1时有

定理3 当R0>1时, 系统(1)在集合Ω上的地方病平衡点是全局渐近稳定的.
证明 因为S*, L*, I*, T*和V*满足

|
所以系统(1)可重新写为
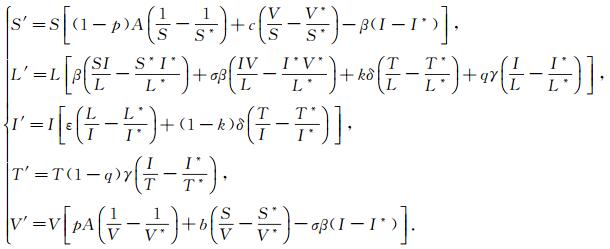
|
(4) |
令

|
(5) |
因此, 关于系统(3)的平衡点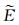
令

|
其中

|
则H2沿着系统(5)的全导数是

|
把S*, L*, I*, T*, V*代入系统(1)中, 再根据其对H′2|(4)进行化简.又因为

|
则有

|
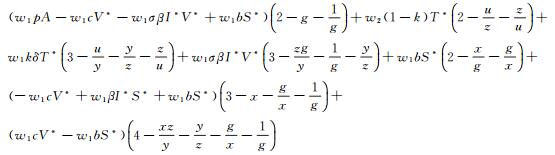
|
因为算术平均数大于等于几何平均数, 所以当x, y, z, u, g>0时, 有H′2|(5)≤0, 当且仅当x=1, g=1, y=z=u时有H′2|(5)=0.
集合{(x, y, z, u, g):x=1, y=z=u, g=1, x, y, z, u, g>0}在z=1时, 符合系统(5)中的第三个等式.因此得出, 系统(5)在集合{(x, y, z, u, g):x=1, y=z=u, g=1, x, y, z, u, g>0}的不变集是一个单点集, 即为{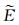
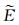
根据传染病动力学的建模思想和肺结核的传播机理建立了具有接种和治疗的肺结核模型, 并分析了模型的动力学性态, 得到疾病传播与否的阈值——基本再生数R0.证明了当R0≤1时, 无病平衡点全局渐近稳定, 疾病最终消亡; 当R0>1时, 存在地方病平衡点, 且其全局渐近稳定, 疾病最终持续.
因此,要控制疾病, 就需减少基本再生数R0使其小于1.由R0的表达式R0= 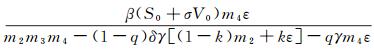


| [1] | TCHUENCHE J M, KHAMIS S A, AGUSTO F B, et al. Optimal control and sensitivity analysis of an influenza model with treatment and vaccination[J]. Acta Biotheoretica, 2011, 59(1): 1-28 DOI:10.1007/s10441-010-9095-8 |
| [2] |
张素霞, 胡刚. 具有治疗控制的传染病模型分析[J].
高校应用数学学报, 2014, 29(1): 1-10 ZHANG S X, HU G. The analysis of an epidemic model with treatment[J]. Numerical Mathematics a Journal of Chinese Universities, 2014, 29(1): 1-10 |
| [3] | YANG Y L, TANG S Y, REN X H. Global stability and optimal control for a tuberculosis model with vaccination and treatment[J]. Discrete and continuous dynamical systems series B, 2016, 21(3): 1009-1022 DOI:10.3934/dcdsb |
| [4] | YANG Y L, LI J Q, MA Z E, et al. Global stability of two models with incomplete treatment for tuberculosis[J]. Chaos, Solitons & Fractals, 2010, 43(1): 79-85 |
| [5] |
刘璐菊, 王春娟. 一个有快慢进展的TB模型的全局稳定性分析[J].
数学的实践与认识, 2007, 37(21): 63-69 LIU L J, WANG C J. The stability analysis for a tuberculosis model with fast and slow progression[J]. Mathematics in Practice and Theory, 2007, 37(21): 63-69 DOI:10.3969/j.issn.1000-0984.2007.21.012 |
| [6] | LIU L J, WANG Y. A mathematical study of a TB model with treatment interruptions and two latent periods[J]. Computational and Mathematical Methods in Medicine, 2014, 2014(1): 99-116 |
| [7] |
王峰, 张娟, 马知恩. 带常数输入率TB模型的全局稳定性[J].
工程数学学报, 2004, 21(4): 574-578 WANG F, ZHANG J, MA Z E. Global stability of a TB model with constant recruitment rate[J]. Chinese Journal of Engineering Mathematics, 2004, 21(4): 574-578 |
| [8] |
曾豪, 王稳地, 闫超, 等. 考虑一般发生率的结核病模型的稳定性分析[J].
西南大学学报(自然科学版), 2016, 38(3): 90-96 ZENG H, WANG W D, YAN C, et al. Stability analysis of a tuberculosis transmission model with general incidence[J]. Journal of Southwest University(Natural Science Edition), 2016, 38(3): 90-96 |
| [9] |
李春, 孙丽萍, 曲双红. 可重复感染的肺结核传播模型[J].
郑州轻工业学院学报(自然科学版), 2014, 29(5): 106-108 LI C, SUN L P, QU S H. An epidemic model of tuberculosis repeated infection[J]. Journal of Zhengzhou University of Light Industry(Natural Science), 2014, 29(5): 106-108 |
| [10] | LIU J L, ZHANG T L. Global stability for a tuberculosis model[J]. Mathematical and Computer Modeling, 2011, 54(1): 836-845 |
| [11] | CASTILLO-CHAVEZ C, FENG Z. Global stability of an age-structure model for TB and its applications to optimal vaccination strategies[J]. Mathematical Biosciences, 1998, 151(2): 135-154 DOI:10.1016/S0025-5564(98)10016-0 |
| [12] | BLOWER S M, SMALL P M, HOPEWELL P C. Control strategies for tuberculosis epidemic:New models for old problems[J]. Science, 1996, 273(5274): 497-500 DOI:10.1126/science.273.5274.497 |
| [13] | CASTILLO-CHAVEZ C, FENG Z. To treat or not to treat:The case of tuberculosis[J]. Journal of Mathemtical Biology, 1997, 35(1): 629-656 |
| [14] | CASTILLO-CHAVEZ C, SONG B. Dynamical models of tuberculosis and their applications[J]. Mathematical Biosciences and Engineering, 2004, 1(2): 361-404 DOI:10.3934/mbe |
| [15] | AGUSTO F B. Optimal chemoprophylaxis and treatment control strategies of a tuberculosis transmission model[J]. World Journal of Modeling and Simulation, 2009, 5(3): 163-173 |
| [16] | BHUNU C P, GARIRA M, MUKANDAVIRE Z, et al. Tuberculosis transmission model with chemoprophylaxis and treatment[J]. Bulletin of Mathematical Biology, 2008, 70(4): 1163-1191 DOI:10.1007/s11538-008-9295-4 |
| [17] | Van den DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1): 29-48 |
| [18] | LASALLE J P. The stability of dynamical systems[M]. Philadelphia: SIAM, 1976: 49-78. |



