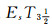 分离性
分离性
 分离性.在加强的
分离性.在加强的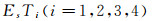 与
与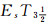 分离性中,分别讨论了其基本性质(即:L-好的推广,弱Es同胚不变性,遗传性,可乘性),并得出
分离性中,分别讨论了其基本性质(即:L-好的推广,弱Es同胚不变性,遗传性,可乘性),并得出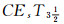 是具有积与上积的范畴.
是具有积与上积的范畴.
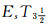 separations in LF topological spaces
separations in LF topological spaces
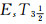 separations are then introduced. In addition, in strong EsTi(i=1, 2, 3, 4) separations and
separations are then introduced. In addition, in strong EsTi(i=1, 2, 3, 4) separations and 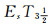 separations, some of their basic properties (such as L-good generalizations, weak Es homeomorphic invariant property, heritability and productivity) are respectively discussed. Alongside that, it can also be concluded that
separations, some of their basic properties (such as L-good generalizations, weak Es homeomorphic invariant property, heritability and productivity) are respectively discussed. Alongside that, it can also be concluded that 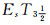 belongs to the category with product and coproduct.
belongs to the category with product and coproduct.
1968年, Chang[1]提出模糊拓扑空间理论, 此后L-fuzzy拓扑空间理论研究达到新高潮.分离性是拓扑学中重要的拓扑性质之一, 在L-fuzzy拓扑空间中, 王国俊[2]和刘应明[3]等已经系统地介绍了分离公理.此外, 国内外许多学者也从不同的角度提出了很多种分离公理, 取得了丰硕的研究成果. 1995年, Kubiak[4]引入了L-T1与Kubiak-T2分离性公理; 之后, 方进明等[5]给出了WTi-(i=0, 1, 2, 3, 4)分离性; 尤飞[6]提出了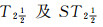
本文在L-fuzzy(其中L是F格)空间中利用更一般的推广型开集Es集给出了更具有一般性的加强的EsTi(i=1, 2, 3, 4)分离性与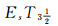
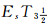
定义1[15]设(LX, δ)是LF拓扑空间, A∈LX,
(1) 若∃U∈δ使得U≤A≤U-, 则称A为半开集;
(2) 若∃F∈δ′使得F°≤A≤F, 则称A为半闭集.
(LX, δ)中一切半开集记为SO(LX), 一切半闭集记为SC(LX).
命题1[16] 设(LX, δ)是LF拓扑空间, A∈LX,
(1) 开集是半开集, 闭集是半闭集;
(2) A是半开集的充要条件为A′是半闭集;
(3) 任意多个半开(闭)集的并(交)是半开(闭)集;
(4) Ao≤Ao≤A≤A-≤A-;
(5) A是半开集的充要条件为A=Ao;
(6) A是半闭集的充要条件为A=A-;
(7) Aoo=Ao;
(8) A--=A-.
定义2 设(LX, δ)是LF拓扑空间, A∈LX,
(1) Es(A)=∧{O∈SO(LX)|A≤O}, 若A满足A=Es(A), 则称A为Es集;
(2) Es*(A)=∨{B∈SC(LX)|B≤A}, 若A满足A=Es*(A), 则称A为Es闭集.
(LX, δ)中一切Es集记为Es(LX), 一切Es闭集记为Es*(LX).
定义3 设(LX, δ)是LF拓扑空间, A∈LX,
(1) 包含于A的一切Es集的并称为A的Es内部, 记为(A)°E, 即

|
(2) 包含A的一切Es闭集的交称为A的Es闭包, 记为(A)E-, 即
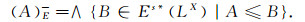
|
命题2 设(LX, δ)是LF拓扑空间, A∈LX,
(1) 任意多个Es集的并(交)仍为Es集;
(2) A是Es集的充要条件为A=(A)Eo;
(3) A是Es闭集的充要条件为A=(A)E-.
证明 (1)要证任意多个Es集的并仍为Es集, 只需证明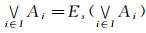
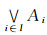
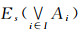
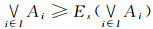
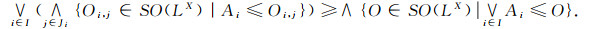
|
对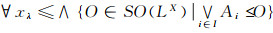
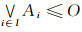
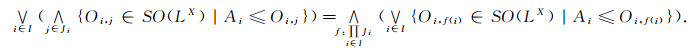
|
对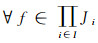
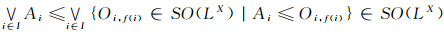
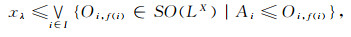
|
从而
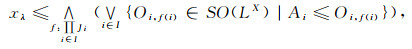
|
于是
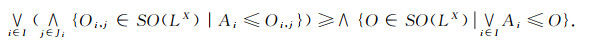
|
要证任意多个Es集的交仍为Es集, 只需证明
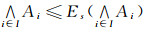
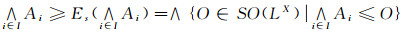
设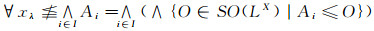
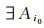

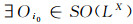
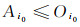

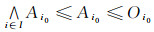
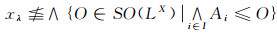
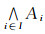
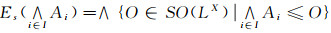
(2) 必要性:当A是Es集时, 由定义3可知, (A)Eo是包含于A的最大Es集, 于是A=(A)Eo.
充分性:由(1)知, (A)Eo是Es集, 又由A=(A)Eo, 于是A是Es集.
(3) 必要性:当A是Es闭集时, 由定义3可知, (A)E-是包含A的最小Es闭集, 于是A=(A)E-.
充分性:由(1)知, (A)E-是Es闭集, 又由A=(A)E-, 于是A是Es闭集.
定义4[2] 设A∈LX, 若∃a∈L, a≠0, 使A(x)>0⇔A(x)≥a, ∀x∈X, 则称A为准分明集.
显然, 分明集都是准分明集, 任一xλ∈M*(LX)也都是准分明集.
定义5 设(LX, δ)是LF拓扑空间, xλ∈M*(LX), P∈Es*(LX).若xλ∉P, 则称P为xλ的Es闭远域.设Q∈LX, 若有xλ的Es闭远域P使Q≤P, 则称Q为xλ的Es远域.分子xλ的一切Es远域和一切Es闭远域之集分别记为eη(xλ)和eη-(xλ).
定义6 设(LX, δ)是LF拓扑空间, A∈LX, P∈Es*(LX).若∀x∈X, 当A(x)>0时, A(x)≤P(x), 则称P为A的Es闭远域.设Q∈LX, 若有A的Es闭远域P使Q≤P, 则称Q为A的Es远域.A的一切Es远域和一切Es闭远域之集分别记为eη(A)和eη-(A).
定义7 设(LX, δ)是LF拓扑空间,
(1) 若对M*(LX)中的任意两个不同的分子xλ与yμ, 当xλ≤yμ时, ∃P∈eη(xλ)使yμ≤P, 则称(LX, δ)为EsT1空间;
(2) 若对M*(LX)中的任意两个分子xλ与yμ, 当x≠y时, ∃P∈eη(xλ)和Q∈eη(yμ)使P∨Q=1, 则称(LX, δ)为Es Hausdorff空间或EsT2空间;
(3) 若对任意一个非零准分明Es闭集A和xλ∈M*(LX), 当x∉suppA时, ∃P∈eη(xλ)和∃Q∈eη(A)使P∨Q=1, 则称(LX, δ)为Es正则空间.称EsT1的Es正则空间为EsT3空间;
(4) 若对任意两个非零准分明Es闭集A和B, 当sup pA∩sup pB=∅时, ∃P∈eη(A)和∃Q∈eη(B)使P∨Q=1, 则称(LX, δ)为Es正规空间.称EsT1的Es正规空间为EsT4空间.
定义8 设(L1X1, δ1)与(L2X2, δ2)是LF拓扑空间, f:L1X1→L2X2, 若L2X2中的任一Es集U, 其原像f-1(U)是L1X1中的Es集, 则称f为Es连续.若映射f是序同态, 则称f为Es连续序同态.
定义9 设(LX1, δ1)与(LX2, δ2)是LF拓扑空间, f:LX1→LX2是L值Zadeh型函数.若存在f是单满的且f与f-1都Es连续, 则称(LX1, δ1)与(LX2, δ2)强Es同胚.称f为强Es同胚映射.被强Es同胚映射所保持的性质称为弱Es同胚不变性质.
定义10 设(LX, δ)是LF拓扑空间, β⊂Es(LX), 若(LX, δ)中任意Es集可以表示为β中若干个Es集之并, 则称β为(LX, δ)的Es基.
定义11 设(X, τ)是分明拓扑空间, L是F格, A:X→L是映射, 若∀a∈L, {x∈X|A(x)≤a}∈Es*(X), 则称A为X上的L值Es下半连续函数.
定理1 设(X, τ)是分明拓扑空间, L是F格, B是X的子集, 则B∈Es(X)的充要条件为χB为X上的L值Es下半连续函数, 此时χB:X→L是B的特征函数.
证明 设a∈L, 当a≠1时, {x∈X|χB(x)≤a}=B′; 当a=1时, {x∈X|χB(x)≤a}=X.由B∈Es(X)知, ∀a∈L, {x∈X|χB(x)≤a}∈Es*(X), 于是χB为X上的L值Es下半连续函数.反之, χB为X上的L值Es下半连续函数, 则∀a∈L, {x∈X|χB(x)≤a}∈Es*(X), 即B′∈Es*(X)或X∈Es*(X), 从而B∈Es(X)或X∈Es(X), 所以定理成立.
2 加强的EsTi(i=1, 2, 3, 4)分离性定义12 设(LX, δ)是LF拓扑空间,
(1) 若每个LF点xλ都是Es闭集, 则称(LX, δ)为SEsT1空间;
(2) 若对任意两个LF点xλ与yμ, 当x≠y时, ∃P∈eη(xλ)和Q∈eη(yμ)使∀x∈X, P(x)=1或Q(x)=1成立, 称(LX, δ)为强Es Hausdorff空间.称SEsT1的强Es Hausdorff空间为SEsT2空间;
(3) 若对任意一个非零准分明Es闭集A和任意一个LF点xλ, 当x∉sup pA时, ∃P∈eη(xλ)和Q∈eη(A)使∀x∈X, P(x)=1或Q(x)=1成立, 则称(LX, δ)为强Es正则空间.称SEsT1的强Es正则空间为SEsT3空间;
(4) 若对任意两个非零准分明Es闭集A和B, 当sup pA∩sup pB=∅时, ∃P∈eη(A)和Q∈eη(B)使∀x∈X, P(x)=1或Q(x)=1成立, 则称(LX, δ)为强Es正规空间.称SEsT1的强Es正规空间为SEsT4空间.
命题3

|
易证.
定义13 设(X, τ)是拓扑空间,
(1) 若对∀x, y∈X, x≠y, ∃P, Q∈Es(X)使x∈P, y∈Q且x∉Q, y∉P, 则称(X, τ)为EsT1空间;
(2) 若对∀x, y∈X, x≠y, ∃P, Q∈Es(X)使x∈P, y∈Q且P∩Q=∅, 则称(X, τ)为EsT2空间;
(3) 若对∀x∈X, A⊂X且x∉A∈Es*(X), ∃P, Q∈Es(X)使x∈P, A⊂Q且P∩Q=∅, 则称(X, τ)为EsT3空间;
(4) 若对∀A, B⊂X且A, B∈Es*(X), A∩B=∅, ∃P, Q∈Es(X)使A⊂P, B⊂Q且P∩Q=∅, 则称(X, τ)为EsT4空间.
定理2 设(LX, ωL(τ))是由分明拓扑空间(X, τ)拓扑生成的LF拓扑空间, 则(LX, ωL(τ))是SEsTi空间的充要条件为(X, τ)是EsTi空间, 其中i=1, 2, 3, 4.
证明 以i=2为例.
必要性:设(LX, ωL(τ))是SEsT2空间, x与y是X中两个不同的点.∀λ∈L, 则有Es闭集P∈eη(xλ)和Q∈eη(yλ)使∀x∈X, P(x)=1或Q(x)=1成立, 从而
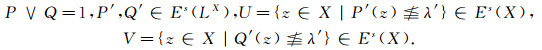
|
因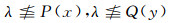
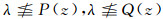
充分性:设(X, τ)是EsT2空间, 从而也是EsT1空间, 于是, (LX, ωL(τ))是SEsT1空间.下面只需证明(LX, ωL(τ))是强Es Hausdorff空间.设xλ与yμ是任意两个LF点且x≠y.因(X, τ)是EsT2空间, 所以∃U, V∈Es(X)使x∈U, y∈V且U∩V=∅.
令P=χU′, Q=χV′, 由x∉U′, y∉V′知, P, Q分别是xλ, yμ的Es闭远域, 且P∨Q=χU′∨χV′=χU′∨V′=χ1=1, 又因P, Q都是分明集, 所以对∀x∈X, 有P(x)=1或Q(x)=1成立, 于是(LX, ωL(τ))是强Es Hausdorff空间, 所以(LX, ωL(τ))是SEsT2空间.
推论1 设(LX, δ)是可拓扑生成的LF拓扑空间, 则(LX, δ)是SEsTi空间的充要条件为它是EsTi空间, 其中i=1, 2, 3, 4.
定理3 SEsTi空间具有遗传性, 即若(LX, δ)是SEsTi空间, Y是X的非空子集, 则(LY, δ|Y)也是SEsTi空间, 其中i=1, 2, 3, 4.
证明 以i=3为例.
设(LX, δ)是SEsT3空间, 对∀y∈X, λ∈L, Y⊂X, A是Y上的任一非零准分明Es闭集和xλ是任一LF点, 且x∉sup pA.设xλ*和A*分别为xλ和A的扩张, 则xλ*为(LX, δ)中的LF点, A*是X上的任一非零准分明Es闭集.因(LX, δ)是SEsT3空间, 所以当x∉sup pA*时, ∃P∈eη-(xλ*)和Q∈eη-(A*)使∀x∈X, P(x)=1或Q(x)=1成立.显然有P|Y∈eη-(xλ)和Q|Y∈eη-(A)且(P|Y)∨(Q|Y)=(P∨Q)|Y=1|Y.又x∉sup pA*, 有x∉sup pA, 又因P|Y和Q|Y是分明集, ∀y∈Y, (P|Y)(y)=1或(Q|Y)(y)=1成立.故(LY, δ|Y)也是SEsT3空间.
定理4 设(LX, δ)是{(LXt, δt)}t∈T的乘积空间, 若∀t∈T, (LXt, δt)是SEsTi空间, 则(LX, δ)是SEsTi空间.反过来, 若(LX, δ)是SEsTi空间, 则∀r∈T, 当(LXr, δr)是满层空间时, (LXr, δr)是SEsTi空间, 其中i=1, 2.
证明 以i=1为例.
设∀t∈T, (LXt, δt)是SEsT1空间, x={xt}t∈T是(LX, δ)上的LF点, 易知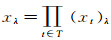
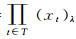
反过来, 设(LX, δ)是SEsT1空间, ∀r∈T, (LXr, δr)是满层空间, 任取一点x={xr}r∈T∈X, 由文献[2]中的定理2.8.9知, (LX, δ)的过点x且平行于(LXr, δr)的LF平面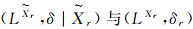
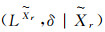
定理5 设(LX1, δ1)与(LX2, δ2)是LF拓扑空间, f:LX1→LX2是强Es同胚映射.若(LX1, δ1)是SEsTi空间, 则(LX2, δ2)也是SEsTi空间, 其中i=1, 2, 3, 4.
证明 以i=2为例.
设y1, y2是(LX2, δ2)中的任意两个LF点, 且y1∧y2=0X2, 则存在(LX1, δ1)的两个LF点x1, x2, 使f(x1)=y1, f(x2)=y2, 且x1∧x2=0X, 由(LX1, δ1)是SEsT2空间, 故P∈eη-(x1)及Q∈eη-(x2), 使P=1X1或Q=1X1.令E=f(P), F=f(Q), 由f是单的Es连续映射知, E∈eη-(y1)及F∈eη-(y2), 且E=1X2或F=1X2, 所以(LX2, δ2)是SEsT2空间.
3
定义14 设(LX, δ)是LF拓扑空间.若对任意一个非零的准分明Es闭集和LF点xλ, 当x∉sup pA时, 存在Es连续的L值Zadeh型函数f:(LX, δ)→I*(L)使xλ≤f-1(0*), A≤f-1(1*), 则称(LX, δ)是完全Es正则空间.称SEsT1的完全Es正则空间为Es-Tychonoff空间或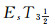
注 设I表示单位区间[0, 1], ε表示I上的通常分明拓扑.由分明拓扑空间(I, ε)拓扑生成的LF拓扑空间(LI, ωL(ε)), 记为I*(L).用t*表示承点为t高度为1的LF点t1.
命题4 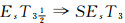
证明 要证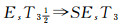
设(LX, δ)是完全Es正则空间, A是非零的准分明Es闭集, xλ是任意一个LF点, 且x∉sup pA时.作Es连续的L值Zadeh型函数f:(LX, δ)→I*(L)使xλ≤f-1(0*), A≤f-1(1*).令P=f-1(χ[1/2, 1]), Q=f-1(χ[0, 1/2]), 则P∈eη-(xλ), Q∈eη-(A), 且P∨Q=f-1(χ[1/2, 1]∨χ[0, 1/2])=f-1(1)=1.因P与Q都是分明集, 所以∀x∈X, P(x)=1或Q(x)=1成立, 故(LX, δ)是强Es正则空间.
引理1 设LF拓扑空间(LX, δ)是完全Es正则空间, 则对任意一个非零的准分明Es闭集A和任意一个LF点xλ, 当x∉sup pA时, 存在分明Es集族μ={Ht|t∈(0, 1)}和分明Es闭集P与Q使
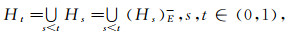
|
(1) |

|
(2) |
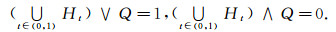
|
(3) |
证明 设(LX, δ)是完全Es正则空间, 则存在Es连续的L值Zadeh型函数f:(LX, δ)→I*(L)使xλ≤f-1(0*), A≤f-1(1*).∀t∈(0, 1), 令Ht=f-1(χ[0, t)), 由χ[0, t)是I*(L)中的Es集且fEs连续知Ht∈Es(LX).同理, ∀t∈(0, 1), 令Gt=f-1(χ[0, t]), 则Gt∈Es*(LX).由s < t知, (Hs)E-≤Gs≤Ht,
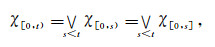
|
由f-1既保并又保交, 故式(1)成立.
令P=f-1(0*), Q=f-1(1*), 则P与Q为Es闭集且式(2)成立.
再由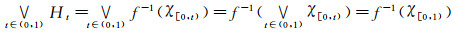
显然, 对于L值Zadeh型函数f而言, 分明集在f之下的原像是分明集, 所以上面的Ht(t∈(0, 1)), P与Q都是分明集.
定理6 设(LX, δ)是满层LF拓扑空间, 则(LX, δ)是完全Es正则空间的充要条件为对任意一个非零准分明Es闭集A和任意一个LF点xλ, 当x∉sup pA时, 存在分明Es集族μ={Ht|t∈(0, 1)}和分明Es闭集P与Q使
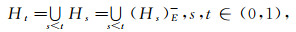
|
(4) |
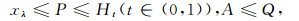
|
(5) |
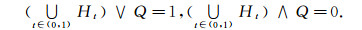
|
(6) |
证明 必要性:由引理1易知.
充分性:定义分明映射f:X→[0, 1]如下:

|
(7) |
由式(6)知, 对∀ν∈X, 都有f(ν)的定义.那么它诱导一个L值Zadeh型函数f:(LX, δ)→I*(L).由式(5)和(7)知f(x)=0, 于是xλ≤P≤f-1(0*).又由式(5)和(7)知f(Q)≤1*, 从而A≤Q≤f-1(1*).下证fEs连续.设B是I*(L)中任意一个Es集, 只需证明f-1(B)∈Es(LX).
① 设B=χ[0, r), 于是f-1(B)是分明集.由B∧1*=0知, f-1(B)∩Q=∅, 此时f-1(B)={ν∈X|f(ν) < r}.设f(ν) < r, 则由式(7)知∃t < r, 使ν∈Ht, 于是f-1(B)⊂Hr.反过来, 设ν∈Hr, 由式(4)知∃t < r, 使ν∈Ht, 所以由式(7)知f(ν)≤t < r, 即f-1(B)=Hr∈Es(LX).
② 设B=χ(s, 1], 于是f-1(B)是分明集且f-1(B)={ν∈X|f(ν)>s}.设ν∈f-1(B), 即f(ν)>s, 取t使f(ν)>t>s, 则ν∉Ht, 于是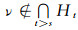

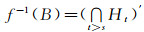


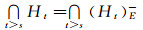
③ 设B=χ(a, b), 且(a, b)⊂[0, 1].因形如[0, t)与(s, 1]的Es集构成ε的子基, 由f-1既保并又保交知f-1(B)∈Es(LX).
④ 设B是I上取常值λ(λ∈L)的LF集, 由(LX, δ)是满层空间以及f是L值Zadeh型函数知f-1(B)∈Es(LX).
⑤ ∀xλ∈I*(L)且x∈(0, 1), 有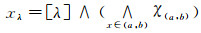
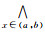
∀B∈I*(L), 有
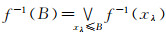
综上, 对∀B∈Es(LI), 有f-1(B)∈Es(LX).
引理2 设f:(X, τ)→(Y, μ)是分明映射, F:(LX, ωL(τ))→(LY, ωL(μ))是它诱导出的L值Zadeh型函数, 则二者之一Es连续的充要条件为另一个Es连续.
证明 设f:(X, τ)→(Y, μ)是Es连续, 则对Y上任意一个Es集G, 有F-1(χG)=χf-1(G)∈Es(LX), 对Y上任意一个常值LF集[r], ∀x∈X, f-1([r])(x)=[r]°f(x)=[r](f(x))=r, f-1([r])是X上取常值的LF集, 于是F-1(A)∈Es(LX), 此时A={rχG|G∈Es(LX), r∈L}是ωL(μ)的Es基.故L值Zadeh型函数F:(LX, ωL(τ))→(LY, ωL(μ))是Es连续.
反之, L值Zadeh型函数F:(LX, ωL(τ))→(LY, ωL(μ))是Es连续, 则对Y上任意一个Es集G, 由χG∈ωL(μ)知F-1(χG)=χf-1(G)∈Es(LX), 则f-1(G)∈Es(X).于是f:(X, τ)→(Y, μ)是Es连续.
定义15 设(X, τ)是拓扑空间.若对∀x∈X, A⊂X且x∉A∈Es*(X), 存在一个Es连续映射f:X→[0, 1]使f(x)=0以及对∀y∈A有f(y)=1, 则称(X, τ)为完全Es正则空间.称EsT1的完全Es正则空间为Es-Tychonoff空间或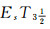
定理7 设(LX, ωL(τ))是由分明拓扑空间(X, τ)拓扑生成的LF拓扑空间, 则(LX, ωL(τ))是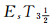
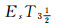
证明 只需证明完全Es正则性成立即可.
必要性:设(LX, ωL(τ))是完全Es正则空间, x∈X, B∈Es(X)且x∉B.令A=χB, 则A是(LX, ωL(τ))中的准分明Es闭集且x∉sup pA, 于是存在Es连续的L值Zadeh型函数f:(LX, ωL(τ))→(LI, ωL(ε))使x1≤f-1(0*), A≤f-1(1*).由引理2知分明映射f:(X, τ)→(I, ε)Es连续.易知, f(x)=0且∀y∈sup pA=B, f(y)=1, 所以(X, τ)是完全Es正则空间.
充分性:设(X, τ)是完全Es正则空间, A是(LX, ωL(τ))中的准分明Es闭集, xλ是X上的LF点且x∉sup pA.令B=sup pA, 由A是准分明Es闭集知B是(X, τ)中的Es闭集.又x∉B, 于是, 存在Es连续函数f:(X, τ)→(I, ε)使f(x)=0且∀y∈sup pA=B, f(y)=1.由引理2知f诱导出的L值Zadeh型函数f:(LX, ωL(τ))→(LI, ωL(ε))Es连续.显然xλ≤f-1(0*), A≤f-1(1*), 故(LX, ωL(τ))是完全Es正则空间.
定理8 设(LX, δ)是由分明拓扑空间拓扑生成的LF拓扑空间, 若(LX, δ)是
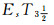
证明 设(LX, δ)是由(X, τ)拓扑生成的, 即δ=ωL(τ).若(LX, δ)是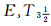
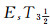
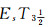
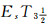
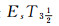
定理9 设(LX, δ)是一族
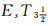
证明 设∀t∈T, δt=ωL(τt), 此时τt是Xt上的分明拓扑, 由定理7知τt是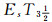
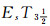

定理10 设(LX1, δ1)与(LX2, δ2)是LF拓扑空间, f:LX1→LX2是强Es同胚映射.若(LX1, δ1)是完全Es正则空间, 则(LX2, δ2)也是完全Es正则空间.
证明 设A是X2上非零的准分明Es闭集, xλ是X2上任意一个LF点, 则存在X1上非零的准分明Es闭集B, X1上LF点yμ, 使f(B)=A, f(yμ)=xλ.因(LX1, δ1)是完全Es正则空间, 当x∉sup pB时, 有Es连续的L值Zadeh型函数g:(LX1, δ1)→I*(L)使yμ≤g-1(0*), B≤g-1(1*).令h=g°f-1, 当f(x)∉sup pA时, h:(LX2, δ2)→I*(L)是Es连续的L值Zadeh型函数, 且f(B)=A, f(yμ)=xλ.于是, xλ=f(yμ)≤f(g-1(0*))=f°g-1(0*)=h-1(0*),
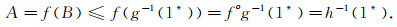
|
所以(LX2, δ2)是完全Es正则空间.
定义16[17] 设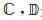
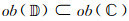
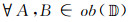
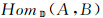
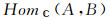
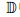
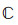



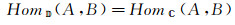

定义17[18] 设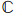
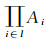
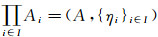
定义18[18] 设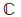
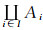
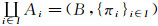
定义19[3] 设{(LXi, δi)}i∈I是一族LF拓扑空间, ∀s, t∈I且s≠t有Xs∩Xt=∅, 令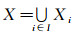
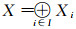
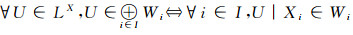
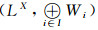
对同一Fuzzy格L, 以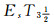
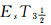
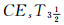
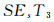
定理11 

证明 由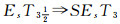
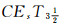
要证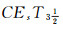
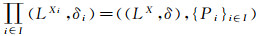
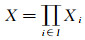
事实上, (1)∀i∈I, Pi∈Hom((LX, δ), (LXi, δi)); (2)对任意的对象D=(LY, ξ)及∀i∈I, σi∈Hom(D, (LXi, δi)), 定义g:Y→X为g(y)={xi}i∈I, 其中xi=σi(y), 令x={xi}i∈I∈X, 设f:LY→LX为g诱导的L值Zadeh型函数, ∀y∈Y, g(y)=x, ∀i∈I, pig(y)=xi=σi(y), 于是pig=σi, 故∀B∈LY, Pi°f(B)(xi)=∨{B(y)|pi°g(y)=xi}=∨{B(y)|σi(y)=xi}=σi(B)(xi), 所以Pif=σi, 又因σi为Es连续的L值Zadeh型函数以及Pi是投影映射与乘积空间的性质知, f为Es连续的L值Zadeh型函数, 易证这样的f是唯一的.于是对∀i∈I, 有交换图图 1成立.
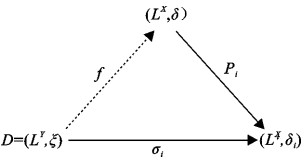
|
| 图 1 交换图 Fig.1 Commuting graph |
定理12 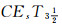
只需证明若{(LXi, δi)}i∈I是一对象集, 对象(LX, δ)与态射集{Pi}i∈I组成的序偶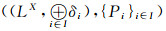
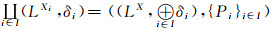
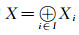
| [1] | CHANG C L. Fuzzy topological spaces[J]. Journal of Mathematical Analysis and Applications, 1968, 24(1): 182-190 DOI:10.1016/0022-247X(68)90057-7 |
| [2] |
王国俊.
LF拓扑空间论[M]. 西安: 陕西师范大学出版社, 1986.
WANG Guojun. L-fuzzy topological space theory[M]. Xi'an: Shaanxi Normal University Press, 1986. |
| [3] | LIU Yingming, LUO Maokang. Fuzzy topology[M]. Singapord: Singapord World Scientific Publishing Co Pte Ltd, 1997. |
| [4] | KUBIAK T. On L-tychonoff spaces[J]. Fuzzy Sets and Systems, 1995, 73(1): 25-53 DOI:10.1016/0165-0114(94)00367-G |
| [5] | FANG Jinming, REN Bailin. A set of separation axiom in LF topological spaces[J]. Fuzzy Sets and Systems, 1998, 96(3): 359-366 DOI:10.1016/S0165-0114(96)00316-8 |
| [6] |
尤飞. 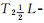 拓扑空间和 拓扑空间和 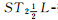 拓扑空间的分离性[J].
模糊系统与数学, 2001, 15(4): 73-76 拓扑空间的分离性[J].
模糊系统与数学, 2001, 15(4): 73-76 YOU Fei. The separation axioms of 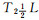 -fts and -fts and 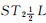 -fts[J].
Fuzzy Systems and Mathematics, 2001, 15(4): 73-76 -fts[J].
Fuzzy Systems and Mathematics, 2001, 15(4): 73-76 |
| [7] |
谷敏强, 赵彬. L-fuzzy拓扑空间的层分离性公理[J].
模糊系统与数学, 2003, 17(3): 12-18 GU Minqiang, ZHAO Bin. Layer separation axioms in L-fuzzy topological spaces[J]. Fuzzy Systems and Mathematics, 2003, 17(3): 12-18 |
| [8] | SHI Fugui. A new approach to L-T2, L-urysohn, and L-completely hausdorff axioms[J]. Fuzzy Sets and Systems, 2006, 157(6): 794-803 DOI:10.1016/j.fss.2005.11.007 |
| [9] |
黄金兰, 陈水利. Lω-空间中的ω-Tychonoff分离性[J].
模糊系统与数学, 2012, 26(4): 43-48 HUANG Jinlan, CHEN Shuili. ω-Tychonoff separation in Lω-spaces[J]. Fuzzy Systems and Mathematics, 2012, 26(4): 43-48 |
| [10] |
杨强, 杨建新. L-fuzzy H-分离性[J].
解放军理工大学学报, 2000, 1(2): 90-95 YANG Qiang, YANG Jianxin. L-fuzzy H-separation[J]. Journal of PLA University of Science and Technology, 2000, 1(2): 90-95 |
| [11] |
王婕, 吕志远. LF拓扑空间的Si-(i=-1, 0, 1, 2)分离性[J].
大学数学, 2003, 19(3): 67-72 WANG Jie, LYU Zhiyuan. Si-(i=-1, 0, 1, 2) separation character in LF topological space[J]. Journal of Mathematics for Technology, 2003, 19(3): 67-72 |
| [12] |
苏淑华, 许兆龙, 杨淑群. LF拓扑空间的正则闭分离性[J].
模糊系统与数学, 2008, 22(1): 85-90 SU Shuhua, XU Zhaolong, YANG Shuqun. Regular closed separation on LF topological space[J]. Fuzzy Systems and Mathematics, 2008, 22(1): 85-90 |
| [13] |
苏淑华, 许兆龙, 杨淑群. LF拓扑空间的rT-分离性[J].
模糊系统与数学, 2009, 23(6): 80-84 SU Shuhua, XU Zhaolong, YANG Shuqun. rT-separation in LF topological space[J]. Fuzzy Systems and Mathematics, 2009, 23(6): 80-84 |
| [14] |
张春燕. LF拓扑空间中一类加强的分离性[J].
五邑大学(自然科学版), 2010, 24(1): 57-60 ZHANG Chunyan. A kind of strong separation axiom in L-topological spaces[J]. Journal of Wuyi University(Natural Science Edition), 2010, 24(1): 57-60 |
| [15] | AZAD K K. On fuzzy semi-continuity, fuzzy almost continuity and fuzzy weakly continuity[J]. Journal of Mathematical Analysis and Applications, 1981, 82(1): 14-32 DOI:10.1016/0022-247X(81)90222-5 |
| [16] |
吴广庆, 杜萍. L-Fuzzy拓扑空间中的半内部, 半闭包, 半边界, 半正则性质[J].
哈尔滨科学技术大学学报, 1996, 20(2): 95-99 WU Guangqing, DU Ping. On the properties of semi-interior, semi-closure, semi-boundary and semi-regular in a L-Fuzzy topological space[J]. Journal Harbin University and Technology, 1996, 20(2): 95-99 |
| [17] |
郑崇友, 樊磊, 崔宏彬. Frame与连续格[M]. 2版. 北京: 首都师范大学出版社, 2000.
ZHENG Chongyou, FAN Lei, CUI Hongbin.Frame and continuous lattice[M].2nd Edition.Beijing:Capital Normal University Press, 2000. |
| [18] |
周伯壎.
同调代数[M]. 北京: 科学出版社, 1999.
ZHOU Boxun. Homological algebra[M]. Beijing: Science Press, 1999. |



