半群理论研究近年来取得了长足发展, 涉及到多类半群, 诸如C0半群、C-半群、积分半群、广义半群等, 国内外众多研究者对此也作了大量工作.文献[1]研究了C-半群的紧性, 给出了单参数C-半群的紧性概念.文献[2-9]引入了双参数C0半群及其无穷小生成元的定义, 讨论了双参数C0半群的一些性质, 如收敛性、范数连续性等.其后有许多学者对此也做了相应的研究.文献[10-13]对半群的拟紧性、直接紧性等作了一些探讨.文献[14-17]对双连续半群, 压缩半群及半群的扰动等作了讨论.由此, 单参数半群的理论研究变得更为丰富, 研究的方向也逐步拓展到双参数的情形.然而, 与单参数半群的理论研究相比较, 双参数半群的相应理论研究还存在些不足, 有待进一步研究.本文依据C0半群, 把单参数变为双参数, 将C0半群一些好的结论, 应用到双参数半群, 给出了双参数C0半群紧的定义, 得到了双参数C0半群的紧性性质.从而进一步完善了双参数C0半群的相关理论体系.
1 主要定义设X为Banach空间, B(x)表示X中有界算子全体构成的空间.I∈B(X)为恒等算子, L(X)表示X到自身的线性算子所构成的空间.
定义1[6] 若算子族(T(t, s))t, s≥0∈B(x)满足
(a) T(0, 0)=I;
(b) T((t1, s1)+(t2, s2))=T(t1, s1)T(t2, s2), ∀, t1, s1, t2, s2≥0;
(c) 映射(t, s)|→T(t, s)x强连续, ∀, t, s≥0, x∈X.
则称其为双参数C0半群.
定义2[6] 双参数C0半群(T(t, s))t, s≥0的无穷小生成元是线性变换L:R2→L(X), 定义为
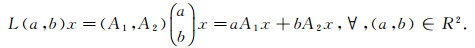
|
其中A1, A2分别为单参数C0半群(T(t, 0))t≥0和(T(0, t))t≥0的无穷小生成元, 即
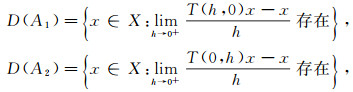
|
且
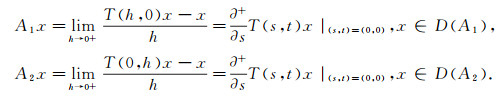
|
定义3 设(T(t, s))t, s≥0是X上的双参数C0半群, 当t>t0, s>s0时, T(t, s)是紧的, 则称双参数C0半群(T(t, s))t, s≥0当t>t0, s>s0时是紧的; 若当t>0, s>0时, T(t, s)是紧的, 则称双参数C0半群(T(t, s))t, s≥0是紧的.
2 主要结果及证明定理1 假定(T(t, s))t, s≥0是双参数C0半群, 且当t>t0, s>s0时, T(t, s)紧的, 则T(t, s)在t>t0, s>s0时按一致算子拓扑连续.
证明 设(T(t, s))t, s≥0是X上的双参数C0半群, 其无穷小生成元是(A1, A2), 则∃ω≥0, M≥1, 使得‖T(t, s)‖≤Mexp(ω(s+t)).当0≤t≤1, 0≤s≤1时, 有
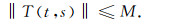
|
∀ε>0, 当t>t0, s>s0时, Ut≡{T(t, s)x}是紧集.因此, 存在有限个点x1, x2, …xn∈Ut, 使得以xi(i=1, 2, …n.)为中心, 以
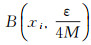

|
从而对x∈Ut, 取i∈{1, 2, …n}, 使得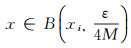
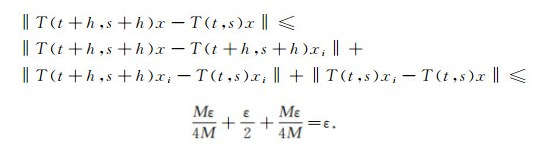
|
则T(t, s)在t>t0, s>s0时按一致算子拓扑连续.
定理2 设(T(t, s))t, s≥0是X上的双参数C0半群, 其无穷小生成元是(A1, A2), 令A=(A1, A2)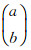
证明 设‖T(t, s)‖≤Mexp(ω(t+s)), ω≥0, M≥1, t, s≥0,
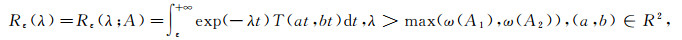
|
由定理1可知, T(t, s), t>0, s>0按一致算子拓扑连续.又T(t, s), t>0, s>0是紧的, 所以Rε(λ)也是紧的.
又因
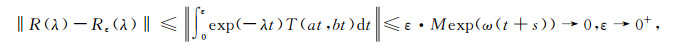
|
从而R(λ; A)作为紧线性算子的一致极限也是紧的.
由预解方程
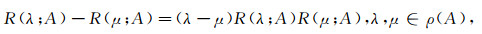
|
可知若R(λ; A)对某一λ∈ρ(A)是紧的, 那么R(λ; A)对任意λ∈ρ(A)都是紧的.
定理3 设(T(t, s))t, s≥0是X上的双参数C0半群, 其无穷小生成元是(A1, A2), 令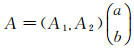
证明 设‖T(t, s)‖≤Mexp(ω(t+s)), ω≥0, M≥1, t, s≥0, 因
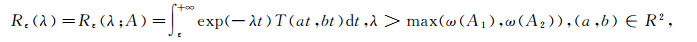
|
则有
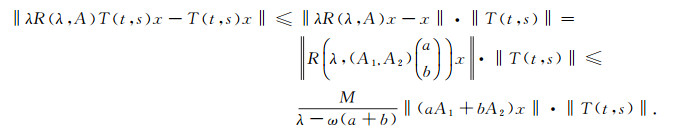
|
由于T(t, s)有界, 从而
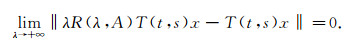
|
又因为R(λ; A)是紧的, λ∈ρ(A), 所以λR(λ, A)T(t, s)是紧的, 从而(T(t, s))t, s≥0作为紧算子的极限也是紧的, 即双参数C0半群(T(t, s))t, s≥0是紧的.
推论1 设(T(t, s))t, s≥0是X上的双参数C0半群, 其无穷小生成元是(A1, A2), 令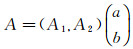
| [1] |
赵华新, 崔志民, 赵国有. C-半群的紧性[J].
延安大学学报(自然科学版), 2000, 19(3): 5-7 ZHAO Huaxin, CUI Zhimin, ZHAO Guoyou. The compact of C-semigroups[J]. Journal of Yan'an University(Natural Science Edition), 2000, 19(3): 5-7 |
| [2] |
秦喜梅. 关于双参数C0半群的一些结果[J].
安徽工程科技学院学报(自然科学版), 2006, 21(4): 66-68 QIN Ximei. Some results of two-parameter C0 semigroups[J]. Journal of Anhui University of Technology and Science(Natural Science Edition), 2006, 21(4): 66-68 |
| [3] |
徐强. 关于双参数C0半群的一些结果[J].
河南科学, 2012, 30(11): 1564-1567 XU Qiang. Some results of two-parameter C0 semigroups[J]. Henan Science, 2012, 30(11): 1564-1567 DOI:10.3969/j.issn.1004-3918.2012.11.002 |
| [4] |
宋学力, 彭济根. 扰动双参数C0半群的直接范数连续性[J].
数学的实践与认识, 2010, 40(2): 218-222 SONG Xueli, PENG Jigen. Immediate norm continuity of perturbed two-parameter C0 semigroups[J]. Mathematics in Practice and Theory, 2010, 40(2): 218-222 |
| [5] | ARORA S C, SHARDA S.On two-parameter semigroups of operators[C]//Lecture Notes in Mathematics Proceeding of a Conference Held in Memory of U N Singh.New Delhi:University of Delhi, 1990:147-153. |
| [6] | SHARIF A S, KHALIL R. On the generator of two-parameter semigroups[J]. Applied Mathematics and Computation, 2004, 156(2): 403-414 DOI:10.1016/j.amc.2003.07.038 |
| [7] |
黄翠, 王彩侠, 宋晓秋, 等. 双参数C-半群及其应用[J].
山东大学学报(理学版), 2013, 48(10): 14-18 HUANG Cui, WANG Caixia, SONG Xiaoqiu, et al. Two parameter C-semigroups and application[J]. Journal of Shandong University(Natural Science Edition), 2013, 48(10): 14-18 |
| [8] | LAWSON J A, ROBBIE D A. Two-parameter semigroups[J]. Semigroup Forum, 2006, 72(1): 15-35 DOI:10.1007/s00233-005-0559-0 |
| [9] | PAZY A. Semigroups of linear operators and application to partial differential equations[M]. New York: Spring-Verlag, 1983. |
| [10] |
郑福, 王佳妮. 半群的拟紧性和不可约性[J].
高校应用数学学报A辑, 2015, 30(1): 84-90 ZHENG Fu, WANG Jiani. Quasi-compactness and irreducibility of the operator semigroups[J]. Applied Mathematics Journal of Chinese Universities(Ser A), 2015, 30(1): 84-90 |
| [11] |
宋学力, 张彦周, 彭济根. Hille-Yosida算子非线性Lipschitz扰动半群的直接紧性[J].
数学的实践与认识, 2015, 45(16): 290-294 SONG Xueli, ZHANG Yanzhou, PENG Jigen. Immediate compactness of nonline lipschitz perturbed semigroups of Hille Yosida operators[J]. Mathematics in Practice and Theory, 2015, 45(16): 290-294 |
| [12] | BREMDLE S, NAGEL R, POLAND J. On the spectral mapping theorem for perturbed strongly continuous semigroups[J]. Archiv der Mathematik, 2000, 74(5): 365-378 DOI:10.1007/s000130050456 |
| [13] | GUO Xiaojiang. The ideal extension property in compact semigroups[J]. Semigroup Forum, 2003, 66(3): 368-380 DOI:10.1007/s002330010134 |
| [14] | JUANG M. On the relationship between perturbed semigroups and their generators[J]. Semigroup Forum, 2000, 61(2): 283-297 DOI:10.1007/PL00006025 |
| [15] | FARLAS B. Adjoint bi-continuous semigroups and semigroups on the space of measures[J]. Czechoslovak Mathematical Journal, 2011, 61(2): 309-322 DOI:10.1007/s10587-011-0076-0 |
| [16] | WANG Xueping. Uniform time-decay of semigroups of contractions[J]. Integral Equations and Operator Theory, 2012, 73(1): 3-4 DOI:10.1007/s00020-011-1930-z |
| [17] | CUI Ranran, LUO Yanfeng. Gelfand-Kirillov dimension of some primitive abundant semigroups[J]. Indian Journal of Pure and Applied Mathematics, 2013, 44(6): 809-822 DOI:10.1007/s13226-013-0044-5 |



