恒化器(Chemostat)可以用来模拟一个简单的湖泊, 污水处理系统以及商业生产的发酵过程等.恒化器模型[1-8]的研究一直是生物和数学工作者所关注的热点课题之一.1950年Monod[1]提出了一类简单的恒化器模型, 但此模型的平衡态仅在驻留时间无限大时成立, 这与实际情况不完全相符,考虑到微生物的死亡, 能量维持, 再循环等实际因素, 文献[2]对由常微分方程描述的恒化器模型进行了详细论述.将文献[2]的恒化器模型添加扩散项和扩散系数得到如下系统(1):
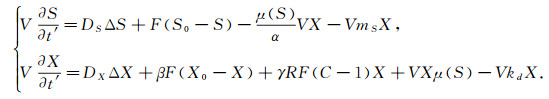
|
(1) |
其中S(x, t′), V(x, t′)分别代表t′时刻营养物与微生物的浓度, mS是能量维持系数, kd是微生物死亡系数, DS, DX是扩散系数.μ(S)被称为反应函数, 其可以采取不同的形式.使用Monod反应函数的研究众多, 文献[3]对文献[2]中的模型作了定性分析, 证明恒化器模型在一定条件下存在一个不稳定的极限环; 文献[4]研究了一类均匀恒化器模型的长时行为, 验证了正平衡解的全局存在唯一性及其稳定性; 文献[5]讨论了一类两种微生物竞争的恒化器模型正平衡解的全局渐近稳定性.但在非理想状下,微生物不可能无限增长,总会达到饱合状态,考虑到此种情况,文献[6]提出了更符合实际情况的反应函数μ(S)=
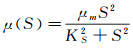
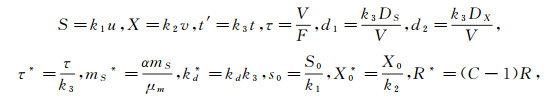
|
其中
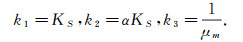
|
不失一般性, 将系统(1)放在齐次Neumann边界条件和初始条件的约束下, 则系统(1)无量纲化为

|
(2) |
其中所有的参数都是正常数, 0≤R≤1, 
系统(2)对应的平衡态问题为
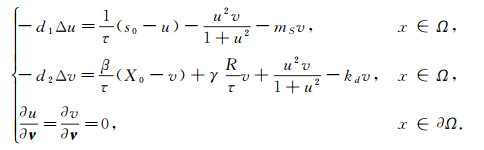
|
(3) |
应用最大值原理[9]和Harnack不等式[10], 给出正解的先验估计.首先研究β=γ=1, 0≤R < 1且X0=0, s0≠0时正常数平衡解的稳定性.
定理1 对于系统(3), 分两种情况:
(1) 当0≤R < 1时, 若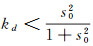

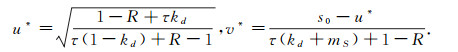
|
(2) 当R=1时, 若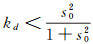
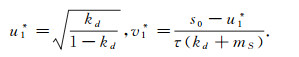
|
引理1 (Harnack不等式)假设c(x)∈ C(Ω), u∈ C2(Ω)∩C1(Ω)是方程
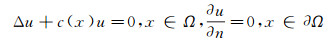
|
的一个非负解, 那么
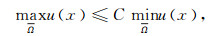
|
其中C是一个仅依赖于Ω和||c||L∞(Ω)的正常数.记λ=(R, kd, s0, τ, ms), 下文所涉及的常数C*, C*都与区域Ω和参数Λ有关.
引理2 对于系统(3)的任意正解(u, v), 由最大值原理知
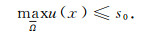
|
定理2 设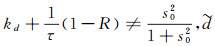


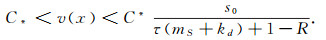
|
证明 令
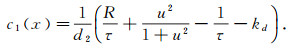
|
由引理2知u(x)≤s0, 将系统(3)的第一个方程加上第二个方程, 然后对得到的等式在Ω上积分得
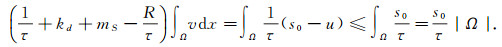
|
由于
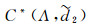
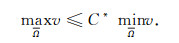
|
则
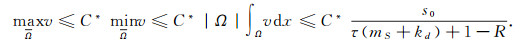
|
v的上界估计已证毕, 下面证明v的下界估计.
假设v(x)>C*不成立, 则存在一个序列{d2j}j=1∞, 满足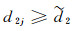
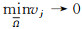
令
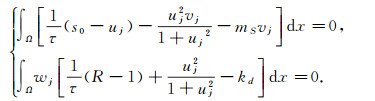
|
(4) |
根据Soblev嵌入定理和文献[11]中椭圆方程的正则性估计可知, 存在{(uj, vj)}j=1∞的一个收敛子序列, 为方便研究仍记为{(uj, vj)}j=1∞, 则当j→∞时, 存在两个非负的函数
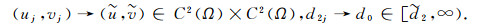
|
容易得到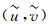
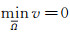
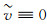

本节主要考虑正常数平衡解的一致渐进稳定性.设0=λ0 < λ1 < λ2 < …→∞是边值问题Δϕ=λϕ, x∈Ω,
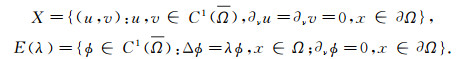
|
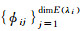
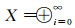
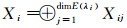
记
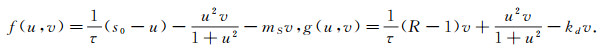
|
f(u, v), g(u, v)在正平衡解(u*, v*)处关于u, v的偏导数为
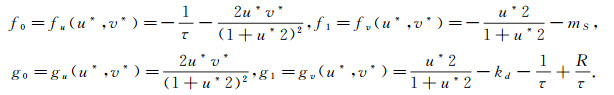
|
系统(3)在(u*, v*)处的线性化算子为
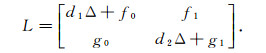
|
定理3 对于系统(3)且0≤R < 1时, 若
证明 当条件成立时, f0 < 0, f1 < 0, g0>0, g1=0.Xi在算子L的作用下是不变的, 且ξ是L在Xi上的特征值当且仅当ξ是矩阵Ai的特征值, 其中

|
记
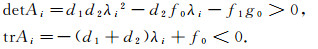
|
因此, 只需证明Ai的两个特征值ξi+, ξi-的实部均为负值.下面具体证明存在不依赖于i的正常数ε, 使得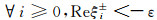
(1) 当i=0时, λ0=0.
若f02+4f1g0≤0, 则Reξ0±=f0/2 < 0;
若f02+4f1g0>0, 则
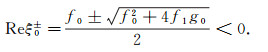
|
(2) 当i≥1时, λi是关于i递增的, 且当i→+∞时, λi→+∞.
若(trAi)2-4trAi≤0, 则
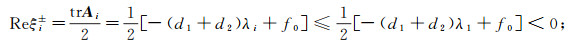
|
若(trAi)2-4detAi>0, 则

|
由以上讨论可知存在一个与i无关的正常数ε, 使得∀i≥0, Reξi± < -ε, 从而由算子L的特征值所组成的算子谱位于{Reξ < -ε}, 由文献[13]中的定理5.1.1可知, 系统(3)在正平衡解E*(u*, v*)处一致渐近稳定.定理3得证.
3 正平衡解的全局渐近稳定性本节主要通过构造Lyapunov函数来证明正常数平衡解的全局渐近稳定性.
引理3 对于系统(3)且0≤R < 1时.
(ⅰ)当τ(kd+mS)≥R且τmS < R < 1时, 存在一常数D满足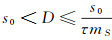
(ⅱ)当τ(kd+mS) < R时, 存在一常数D满足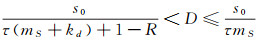
证明 由第一节讨论知u(x), v(x)都是非负的.定义直线l:=u+v-D=0, 其中D是定义的一常数.事实上
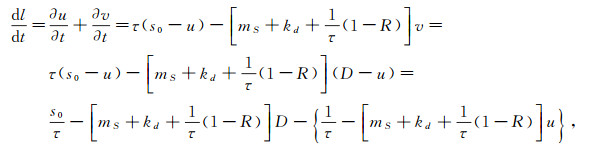
|
为使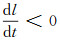

可能会出现两种情况:
(a) 若1-[τ(mS+kd)+1-R]≤0, 即τ(kd+mS)≥ R, 则
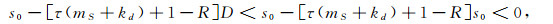
|
所以
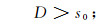
|
(b) 若1-[τ(mS+kd)+1-R]>0, 即τ(kd+mS) < R, 则
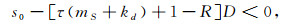
|
所以
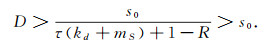
|
由上所述, 若D满足(ⅰ), (ⅱ)中的条件, 必有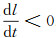
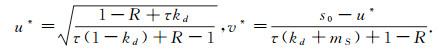
|
对于情况(ⅰ):由于τ(kd+mS)≥R且τmS < R < 1.若对于所有符合情况的D都满足

|
则

|
即说明了E*(u*, v*)在γ内.
对于情况(ⅱ):由于τ(kd+mS) < R.若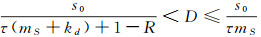
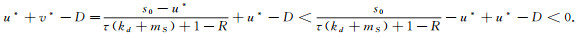
|
再次说明了E*(u*, v*)在γ内.引理得证.
结合文献[14]中不变子集区域理论, 以此来证明系统(3)的全局渐近稳定性.
定理4 对于系统(3)且0≤R < 1时, 若满足条件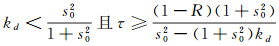
证明 受文献[15-16]的启发, 构造一个Lyapunov函数.
令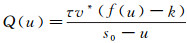
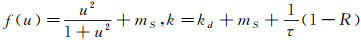
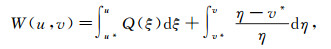
|
则Lyapunov函数是E(t)=∫ΩWdx.
若微分函数h(u)且u满足齐次Neumann边界条件, 则
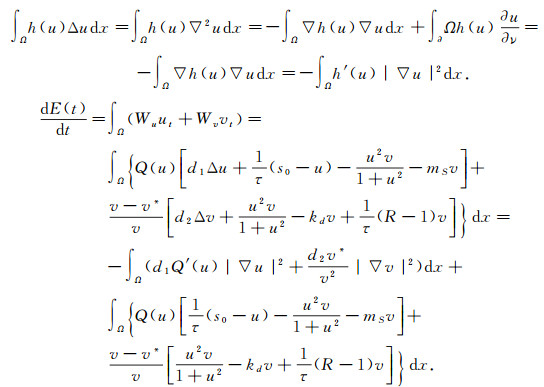
|
由于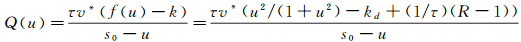
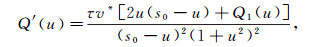
|
其中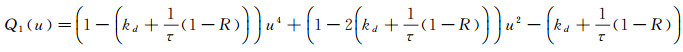
Q1(u)可以看作u2的一元二次函数且二次项系数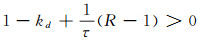

记
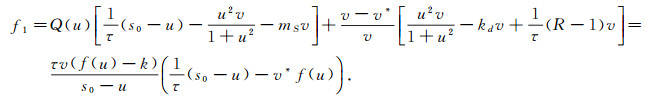
|
下面证明f1≤0成立.利用反证法, 假设f1>0, 则有两种情况:
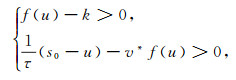
|
(5) |
或
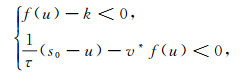
|
(6) |
先证明式(5)的情况不成立.由于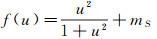
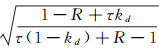

|
矛盾, 故式(5)不成立.
再证明式(6)的情况不成立, 假定其成立, 对于式(5)中的第一式f(u) < k=f(u*), 则0 < u < u*, 而由第二式可知
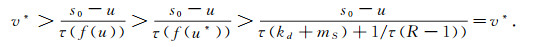
|
矛盾, 故式(6)不成立.
综上所述, f1≤0, 则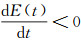
对于β=γ=1, R=1且X0=0, s0≠0时的情况, 即理想状态下的恒化器模型的平衡解的稳定性.由上述的方法同理可证得以下结论.
定理5 对于系统(3)且R=1时, 若
引理4 对于系统(3)且R=1时.
(ⅰ)当τ(kd+mS)≥ 1且τmS < 1时, 存在一常数D满足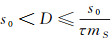
(ⅱ)当τ(kd+mS) < 1时, 存在一常数D满足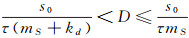
定理6 对于系统(3)且R=1时, 若满足条件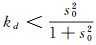
| [1] | MONOD J. La technique de culture continue.Théorie et applications[J]. Ann Inst Pasteur, 1950, 79(2): 390-410 |
| [2] | NELSON M I, KERR T B, CHEN X. A fundamental analysis of continuous flow bioreactor and membrane reactor models with death and maintenance included[J]. Asia-Pac J Chem Eng, 2008, 3(1): 70-80 DOI:10.1002/(ISSN)1932-2143 |
| [3] | ZHANG Tonghua. Global analysis of continous flow bioreactor and membrane reactor models with death and maintenance[J]. J Math Chem, 2012, 50(1): 2239-2247 |
| [4] | CHEN Zhenzhen, ZHANG Tonghua. Long time behaviour of a stochastic model for continuous flow bioreactor[J]. J Math Chem, 2013, 51(1): 451-464 |
| [5] | SUN Shulin, SUN Yaru, ZHANG Guang, et al. Dynamical behavior of a stochastic two-species Monod competition chemostat model[J]. Applied Mathematics and Computation, 2017, 298(1): 153-170 |
| [6] | MURRAY J D.Mathematical biology I:An introduction[M].3rd edition.Berlin:Springer-Verlag, 2002. |
| [7] |
院振军, 李艳玲. 一类非均匀恒化器食物网的共存态[J].
纺织高校基础科学学报, 2010, 23(4): 427-432 YUAN Zhenjun, LI Yanling. Coexistence states for a food web in an un-stirred chemostat[J]. Basic Sciences Journal of Textile Universities, 2010, 23(4): 427-432 |
| [8] |
黄正阳, 李艳玲. C-M型反应函数的非均匀恒化器竞争模型的全局分歧[J].
纺织高校基础科学学报, 2013, 26(4): 450-457 HUANG Zhengyang, LI Yanling. Global bifurcation for a competition model in the unstirred chemostat with the C-M functional response[J]. Basic Sciences Journal of Textile Universities, 2013, 26(4): 450-457 |
| [9] | LOU Yuan, NI Weiming. Diffusion, self-diffusion and cross-diffusion[J]. Journal of Differential Equations, 1996, 131(1): 79-131 DOI:10.1006/jdeq.1996.0157 |
| [10] | LIN Changshou, NI Weiming, TAKAGI Izumi. Large amplitude stationary solutions to a chemotaxis system[J]. Journal of Differential Equations, 1988, 72(1): 1-27 DOI:10.1016/0022-0396(88)90147-7 |
| [11] | GILBARG D, TRUDINGER N S. Elliptic partial differential equation of second order[M]. Beijing: Science Press, 1990: 1-48. |
| [12] |
叶其孝, 李正元, 王明新, 等.
反应扩散方程引论[M]. 北京: 科学出版社, 2011.
YE Qixiao, LI Zhengyuan, WANG Mingxin, et al. Introduction to reaction-diffusion equations[M]. Beijing: Science Press, 2011. |
| [13] | REURY D.Geometric theory of semlinear parabolic equations[M]//Lecture Notes to Mathematics.New York:Springer-Verlag, 1993. |
| [14] | WEINBERGER H F. Invariant sets for weakly coupled parabolic and elliptic systems[J]. Rend Mat, 1975, 8(1): 295-310 |
| [15] | HSU S B. A survey of constructing lyapunov functions for mathematical models in population biology[J]. Taiwanese J Math, 2005, 9(2): 151-173 DOI:10.11650/twjm/1500407791 |
| [16] | HATTAF K, YOUSF N. Global stability for reaction-diffusion equations in biology[J]. Comput Math Appl, 2013, 66(8): 1488-1497 DOI:10.1016/j.camwa.2013.08.023 |



