人类嗜T淋巴细胞病毒Ⅰ型(HTLV-Ⅰ)是第一个被发现的人类逆转录病毒, 通过性接触、输血、母婴和母乳喂养等方式进行传播, 主要感染CD4+T细胞.HTLV-Ⅰ是相关性脊髓病(HAM)或热带痉挛性瘫痪病(TSP)的病原体, HAM/TSP是中枢神经系统的慢性炎性疾病, 迄今为止, HAM/TSP的发病机制尚不清楚, 也缺乏有效的治疗方法[1-3].在感染的细胞中, 整合的病毒DNA称为前病毒, HTLV-Ⅰ感染者在外周血淋巴细胞(PBLs)中具有很高的前病毒负荷, 并且HAM/TSP患者具有高水平的HTLV-1特异性CD8+细胞毒性T淋巴细胞(CTLs), 有研究发现高水平的CTLs及其细胞毒性可能是HAM/TSP患者炎症反应的原因[4].近几十年来, 有关HTLV-Ⅰ的研究已经引起了许多学者的注意, 提出了许多有意义的数学模型[5-15].Horacio Gómez-Acevedo[5]等建立了一个二维模型, 该模型考虑到了HTLV-Ⅰ的垂直传播(有丝分裂), 并分析了此模型的动力学性质.王彩霞等[6]在此基础上建立了一个具有健康CD4+T细胞密度制约的HTLV-Ⅰ模型, 通过全局性态分析证明了后向分支在一定条件下发生.但以上两个模型只有健康细胞和感染细胞两个仓室, 不能体现出病毒的持续感染.之后有学者提出了带有潜伏仓室的HTLV-Ⅰ感染模型[7-9], 但随着研究的深入, 人们发现CTL免疫反应对HTLV-Ⅰ感染的影响很大, 即使考虑了潜伏感染仓室也不能很好的描述病毒感染人体后的情况, 因此一些学者研究了引入免疫反应的HTLV-Ⅰ感染模型[10-15].文献[10-12]提出带有CTL仓室的三维模型, 分析了模型的动力学性质, 说明了CTL免疫反应对HTLV-Ⅰ病毒感染的影响.还有一些学者在此基础上研究了带有时滞的模型[13-15].引入免疫反应的模型说明了宿主免疫反应与病毒持续性感染的动力学相互作用, 但这些模型几乎考虑都是常数输入, 这种假设只有当病毒传播速度较快, 宿主体内环境不变的情况下合理.本文在前人的基础上建立一个包含健康细胞、潜伏感染细胞及CTL免疫反应的三维模型, 并且假定新的健康CD4+T细胞以Logistic形式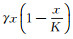
基于传染病仓室模型理论, 建立HTLV-Ⅰ仓室模型.x, y, z分别表示健康的CD4+T细胞的数量、感染的CD4+T细胞的数量及HTLV-Ⅰ特定CD8+T细胞(免疫细胞)的数量.γ是自然增长固有比率, K是健康CD4+T细胞的承载能力, β是传播系数, p是CTL介导溶解比率(每个CD8+T细胞杀死被感染细胞的比率), ν是细胞毒素反应性(特定CTL细胞遇到一个被感染细胞之后的平均增值比率).μ1, μ2分别表示感染细胞, 特定CD8+T细胞的移出率.这样, 可以得到模型Ⅰ,即
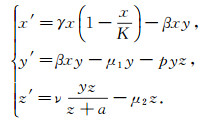
|
对于模型Ⅰ有下面的结论.
定理1 模型Ⅰ的解(x(t), y(t), z(t)), 对于所有的t>0是非负有界的.
证明 从模型Ⅰ的方程中可以得到

|
根据文献[16]中的引理2, 模型Ⅰ的非负初始条件的解对于所有t>0是非负的.
由模型Ⅰ的第一个方程可得到
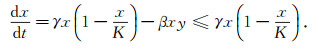
|
由比较原理, 有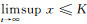
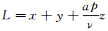
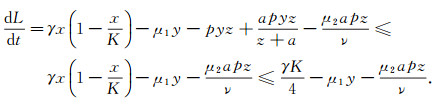
|
如果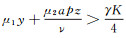
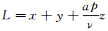
设M是函数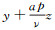
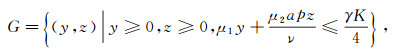
|
这样得到模型Ⅰ的不变集

|
下面来求模型的平衡点.
模型Ⅰ总是存在平衡点P=(0, 0, 0)和无病平衡点P0=(K, 0, 0), 定义基本再生数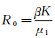
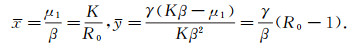
|
P2=(x*, y*, z*)满足
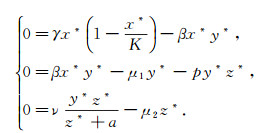
|
(1) |
由式(1)可以得到
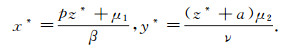
|
(2) |
而式(1)的第一个方程可以得到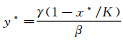
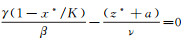
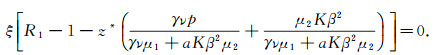
|
(3) |
其中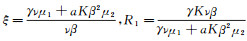
定理2 如果R0≤1, 存在平衡点P, P0; 如果R0>1且R1≤1, 存在平衡点P, P0, P1; 如果R1>1, 存在平衡点P, P0, P1, P2.
3 平衡点的全局稳定性下面将讨论模型Ⅰ平衡点的全局稳定性.
定理3 对于模型Ⅰ有如下结论:
(1) 平衡点P是不稳定的;
(2) 如果R0≤1, P0是全局渐近稳定的;
(3) 如果R0>1且R1≤1, P0不稳定, P1是全局渐近稳定的;
(4) 如果R1>1, P0, P1不稳定, P2是全局渐近稳定的.
证明 (1)模型Ⅰ的线性系统在平衡点P的特征方程为
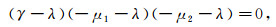
|
由Routh-Hurwitz判据可知平衡点P不稳定.
(2) 取Lyapunov函数V1=y, 沿着模型Ⅰ求导, 得
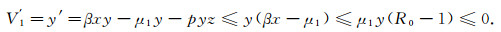
|
这说明当R0≤1时, 对于所有的t>0, 有V′1≤0, V′1=0只在P0点成立.由LaSalle不变原理可知V1=y当R0<1时是减函数, 并且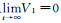
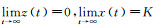
(3) 取Lyapunov函数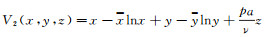
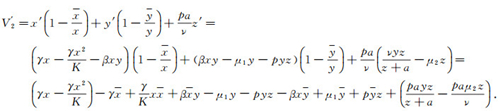
|
将
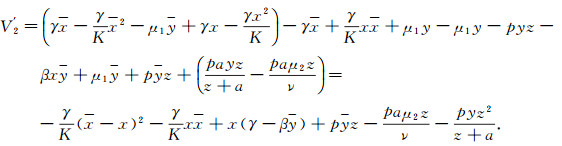
|
将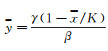

|
即当R1≤1时V′2≤0, V′2=0只在x=x, y=y, z=0时成立.由LaSalle不变原理可知P1是全局渐近稳定的.
(4) 取Lyapunov函数V3=x-x*lnx+y-y*lny+ 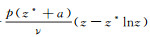
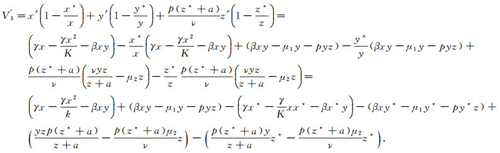
|
将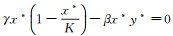

|
将βx*y*=μ1y*+py*z*以及

|
将βx*=μ1+pz*带入, 有
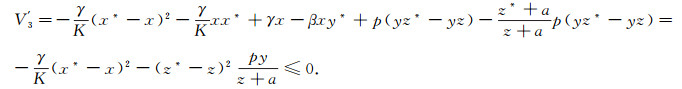
|
V′3=0只在x=x*, y=y*, z=z*时成立, 因此由LaSalle不变原理可知当R1>1时P2是全局渐近稳定的.
4 结束语建立了一个具有logistic增长的HTLV-Ⅰ传染模型, 定理3给出了系统Ⅰ的全局动力学性态.阈值R0决定了HTLV-Ⅰ感染是否为慢性感染, 阈值R1决定了持续CTL免疫反应是否能保持.当R0≤1时无病平衡点P0是全局渐近稳定的, HTLV-Ⅰ消亡; 由于HAM/TSP病人具有高水平的前病毒负荷, 因此R1是区别无症状携带者(asymptomatic carriers)与HAM/TSP的重要参数.当R0>1且R1≤1时P1是全局稳定的, HTLV-Ⅰ感染为低水平前病毒负荷慢性感染, 此时系统可以描述无症状携带者; 当R1>1时P2是全局稳定的, HTLV-Ⅰ感染为高水平前病毒负荷慢性感染, 导致持续的CTL免疫反应, 此时系统可以描述HAM/TSP患者.从前面的讨论, 可以得到R1<1 ⇔y<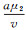
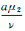
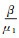
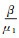
| [1] |
杨少将. 人类T细胞白血病病毒-1相关成年人T细胞白血病淋巴瘤的治疗进展[J].
国际输血及血液学杂志, 2014, 37(3): 241-245 YANG Shaojiang. Advances in treatment of human T-cell leukemia virus-1 associated T-cell lymphoma in adults[J]. International Journal of Blood Transfusion and Hematology, 2014, 37(3): 241-245 |
| [2] | DAVID G, LEPELLETIER Y, JONES K S, et al. Current concepts regarding the HTLV-1 receptor complex[J]. Retrovirology, 2010, 7(1): 2803-2830 |
| [3] | CARPENTIER A, BAREZ P Y, HAMAIDIA M, et al. Modes of human T cell leukemia virus type 1 transmission, replication and persistence[J]. Viruses, 2015, 7(7): 3603-3624 DOI:10.3390/v7072793 |
| [4] | COOK L B, ELEMANS M, ROWAN A G. HTLV-Ⅰ:Persistence and pathogenesis[J]. Virology, 2013, 435(1): 131-140 DOI:10.1016/j.virol.2012.09.028 |
| [5] | GÓMEZ-ACEVEDO Horacio, LI Michael Y. Backward bifurcation in a model for HTLV-Ⅰ infection of CD4+T cells[J]. Bulletin of Mathematical Biology, 2005, 67(1): 101-114 DOI:10.1016/j.bulm.2004.06.004 |
| [6] |
王彩霞, 王战伟. 一类具有后向分支的HTLV-Ⅰ模型[J].
河南科学, 2011, 29(5): 517-519 WANG Caixia, WANG Zhanwei. Backward bifurcation of a HTLV-Ⅰ model[J]. Journal of Henan Sciences, 2011, 29(5): 517-519 |
| [7] | LI Michael Y, LIM Aaron G. Modeling the role of tax expression in HTLV-Ⅰ persistence in vivo[J]. Bulletin of Mathematical Biology, 2011, 73(12): 3008-3029 DOI:10.1007/s11538-011-9657-1 |
| [8] | LI Sumei, ZHOU Yicang. Global dynamics of an HTLV-Ⅰ model with cell-to-cell infection and mitosis[J]. Abstract & Applied Analysis, 2014(4): 1-12 |
| [9] | GÓMEZ-ACEVEDO Horacio, LI Michael Y. Multi-stability in a model for CTL response to HTLV-Ⅰ infection and its implications to HAM/TSP development and prevention[J]. Bulletin of Mathematical Biology, 2010, 72(3): 681-696 DOI:10.1007/s11538-009-9465-z |
| [10] | LANG J, LI M Y. Stable and transient periodic oscillations in a mathematical model for CTL response to HTLV-Ⅰ infection[J]. Journal of Mathematical Biology, 2012, 65(1): 181-199 DOI:10.1007/s00285-011-0455-z |
| [11] | LIM A G, MAINI P K. HTLV-Ⅰ infection:A dynamic struggle between viral persistence and host immunity[J]. Journal of Theoretical Biology, 2014, 352: 92-108 DOI:10.1016/j.jtbi.2014.02.022 |
| [12] | LI Sumei, ZHOU Yicang. Backward bifurcation of an HTLV-Ⅰ model with immune response[J]. Discrete and Continuous Dynamical Systems-Series B, 2016, 21(3): 863-881 DOI:10.3934/dcdsb |
| [13] |
张侣, 张著洪. 基于双时滞HTLV-Ⅰ病毒模型的稳定性分析[J].
生物数学学报, 2015(2): 333-343 ZHANG Lyu, ZHANG Zhuhong. Stability analysis on a HTLV-Ⅰ virus model with two time delays[J]. Journal of Biomathematics, 2015(2): 333-343 |
| [14] | SUN Xinguo, WEI Junjie. Global dynamics of a HTLV-Ⅰ infection model with CTL response[J]. Electronic Journal of Qualitative Theory of Differential Equations, 2013, 6(40): 1-15 |
| [15] | WANG Jinliang, WANG Kaifa, JIANG Zhichao. Dynamical behaviors of an HTLV-Ⅰ infection model with intracellular delay and immune activation delay[J]. Advances in Difference Equations, 2015(1): 1-17 |
| [16] | YANG Xia, CHEN Lansun. Permanence and positive periodic solution for the single-species nonautonomous delay diffusive models[J]. Computers and Mathematics with Applications, 1996, 32(4): 109-116 DOI:10.1016/0898-1221(96)00129-0 |



