The reaction-diffusion systems describe well the interaction between two populations[1]. And the systems are now used in many fields, such as ecology[2-5], social systems[6-7], turbulent flow in plasmas[8-9], semiconductors[10-12], tumor growth[13] and so on. Self-and cross-diffusion terms are the potential mechanisms of pattern formation. In [14], Gambino and her colleagues studied Turing instability and traveling fronts for a nonlinear reaction-diffusion system with cross-diffusion and they also investigated the Lengyel-Epstein System, Brusselator System and Activator-Inhibitor System[15-17].
The model we studied is from [8]. Diamond et al[18] considered the model of the plasma. For the convenience study of turbulence-shear flow interaction, Carreras et al presented the following improved version in [8]:

|
(1) |
Here 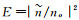




|
(2) |
Del-Castillo-Negrete and Carreras investigated the formation of shear flows with radial structure of the system (2) in [8].
Compared with (2), the following system has rich dynamics
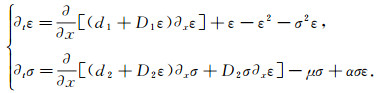
|
(3) |
The definitions for μ and α are the same as which in (2). The analysis of (3) is based on (2), Del-Castillo-Negrete and Carreras studied the turbulence-shear flow interaction in plasmas in [9]. They focused on the three nontrivial fixed points and presented the propagation and segregation of traveling fronts.
In this paper, we are more interested in the system (3).The Turing instability and traveling fronts by weakly nonlinear analysis will be investigated.
1 Linear analysis and Turing instabilityFor the convenience of analyzing, the system (3) is rewritten as follows
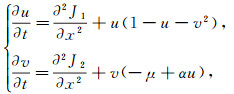
|
(4) |
where
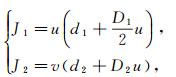
|
here u(x, t), v(x, t) are the substitutions of ε(x, t) and σ(x, t) in (3) respectively, the parameters di, Di(i=1, 2), α and μ are all positive.
The initial conditions and boundary conditions must be added to the above system. As we are interested in the pattern formation in this paper, the homogenous Neuman boundary conditions 
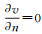
In this part, the possibility of the appearance of the pattern for the system (4) will be investigated. For the system (4), there are four equilibrium points (u*, v*)=(0, 0), (1, 0) and 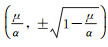

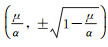
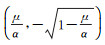
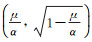
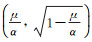
The general form of the linearized system of the system (4) in the neighborhood of (u*, v*) is

|
(5) |
where
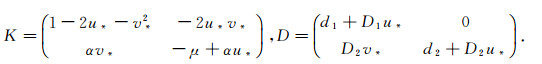
|
(6) |
Looking for the solution of system (4) with the form exp(ikx+λt), we obtain the following dispersion relation

|
where
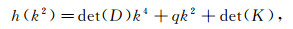
|
(7) |
with
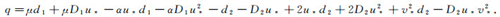
|
(8) |
In the following, we will give the conditions for the formation of the patterns, the critical values of the bifurcation parameter as well as the critical wave number. The stable and unstable conditions will also be investigated.
(Ⅰ) At the L fixed point (1, 0), (6)~(8) can be written as
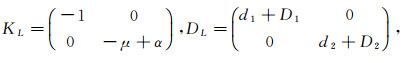
|
with
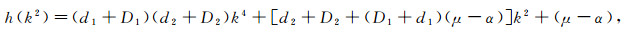
|
and

|
For the reaction system of (4), when α≤μ, it is easy to prove that L fixed point is stable. When diffusion terms are added, then k2(tr(DL)-tr(KL)) > 0, h(k2) > 0 for any k≠0, the full reaction-diffusion system (4) is still stable at (1, 0) under the condition of α≤μ.
(Ⅱ) At the H fixed point 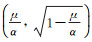


|
(9) |
and

|
(10) |
When 
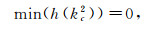
|
(11) |
where
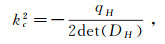
|
which demand that qH is negative. From (10), we know the appearance of the cross-diffusion term D2 destroy the stability of H fixed point.
qH < 0 implies the following condition
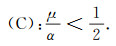
|
In what follows, we use the cross-diffusion coefficient D2 as bifurcation parameter. In order to seek the critical values at which bifurcation occurs.Define
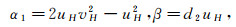
|
and let 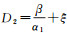
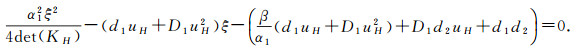
|
(12) |
Then the critical value for bifurcation is
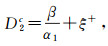
|
(13) |
where ξ+ is the positive root of Eq.(12).
Based on the above analysis, the following theorem can be summarized.
Theorem 1 (ⅰ) The L fixed point is stable for the system (4) under the condition α≤μ; (ⅱ) Assume the conditions (C) and D2 > D2c hold, the H fixed point is spatially unstable for the system (4), where D2c is given by (13).
2 Weakly nonlinear analysis and traveling frontsBy the analysis of Section 1, we know that the H fixed point is Turing unstable and the cross-diffusion term D2 is the key mechanism of pattern formation. However, when the domain is large, one can observe a typical phenomenon that is propagation of the pattern through the physical domain in the form of a traveling wave. In order to quantitatively describe the amplitude of pattern in space, we shall introduce weakly nonlinear analysis[19] and the time scale and spatial scale should be considered. Time scale will be separated into fast scale t and slow time T=ε2t, and time derivative decoupled as ∂t→∂t+ε2∂T. The derivative of spatial is ∂x→∂x+ε∂X, and the reaction diffusion operators are decoupled as ∂xx→ ∂xx+ε∂xX+ε2∂XX. ε is the small control parameter, chosen as 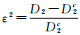
By separating the linear part and the nonlinear part, the original system (4) can be rewritten as follows

|
(14) |
where w is defined in (5) and linear operator is defined as
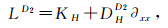
|
where KH and DHD2 are given by (9). For x=(xu, xv), y =(yu, yv) the definition of bilinear operators on vector couple (x, y) are as follows
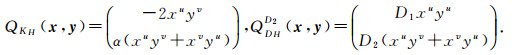
|
By using the asymptotic analysis, D2 and w can be expanded to

|
(15) |
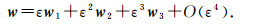
|
(16) |
Then the linear operator LD2 can be expanded as

|
(17) |
and
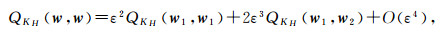
|
(18) |

|
(19) |
Substituting (15)-(19) into (14), according to the order of ε, collecting a series of terms of the equations for wi

|
(20a) |

|
(20b) |
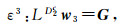
|
where

|
and

|
Under the Neumann boundary condition, the solution of the linear equation (20a) is given by

|
(21) |
The amplitude of the pattern is A(X, T) and the vector ρ is given by the following way
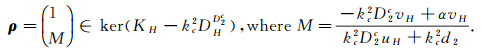
|
Substituting (21) into the right side of F and through calculating, F can be simplified as
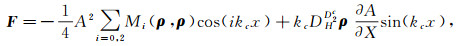
|
where

|
Through the Fredholm alternative, (20b) admits a solution if and only if 〈 F, ϕ 〉=0, where 〈·, ·〉 is the scalar product in 
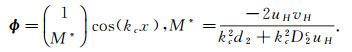
|
(22) |
It is obvious to see that the Fredholm alternative is immediately satisfied. The solution of (20b) is then computed according to the parameters of the full system:

|
(23) |
where the vectors w2i satisfies the linear systems as follows:
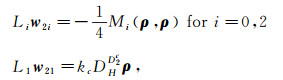
|
with
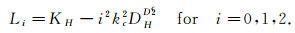
|
Substituting (21) and (23) into the right side of G, then it can be simplified as the following expression

|
with
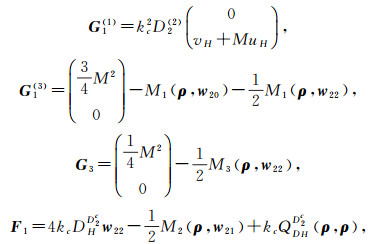
|
where

|
The condition 〈 G, ϕ 〉=0 leads to the equation for amplitude A as follows
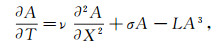
|
(24) |
where
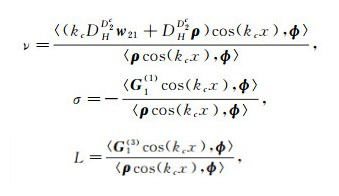
|
and ϕ is given by (22).
The envelope evolution and the progressing of the pattern can be described by the real Ginzburg-Landau equation (24)[20-22], which the exact solution in R is

|
with
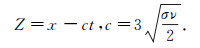
|
This result describes that the traveling front envelop a pattern which diffuses in a spatial domain.
3 ConclusionIn this paper, the model of turbulence shear flow interaction is studied, the cross-diffusion of turbulent flow and shear flow induces the formation of the pattern, and gradually diffuses into the large spatial region. In the reaction-diffusion system, the nonlinear cross-diffusion term is the source of the formation of the pattern. By the linear analysis, it is concluded that diffusion leads to instability, and then the pattern forms. Then by weakly nonlinear analysis, we know that the amplitude of pattern which diffuses as traveling waves in the large spatial region. Of course, the further work is to give numerical simulation that will show a good agreement with the solution prescribed by the weakly nonlinear expansion.
| [1] | MIMURA M, KAWASAKI K. Spatial segregation in competitve interaction-diffusion equation[J]. Journal of Mathematical Biology, 1980, 9(1): 49-64 DOI:10.1007/BF00276035 |
| [2] | GILAD E, VON HARDENBERG J, PROVENZALE A, et al. A mathematical model of plants as ecosystem engineers[J]. Theor Biol, 2007, 244(4): 680-691 DOI:10.1016/j.jtbi.2006.08.006 |
| [3] | TIAN C. Turing patterns created by cross-diffusion for a Holling Π and Leslie-Gower type three species food chain model[J]. Math Chem, 2011, 49(6): 1128-1150 DOI:10.1007/s10910-011-9801-z |
| [4] | ZHANG J, LI W, WANG Y. Turing patterns of a strongly coupled predator-prey system with diffusion effects[J]. Nonlin Anal, 2011, 74(3): 847-858 DOI:10.1016/j.na.2010.09.035 |
| [5] | PENG Y H, ZHANG T H. Turing instability and pattern induced by cross-diffusion in a predator-prey system with Allee effect[J]. Applied Mathematics and Computation, 2016, 275: 1-12 DOI:10.1016/j.amc.2015.11.067 |
| [6] | EPSTEIN J M. Nonlinear dynamics[J]. Mathematical Biology, and Social Science, Complexity, 1997, 3(2): 50-51 |
| [7] | YIZHAQ H, PORTNOV B, MERON E. A mathematical model of segregation patterns in residential neighbourhoods[J]. Environ Plan A, 2004, 36(1): 149-172 DOI:10.1068/a35274 |
| [8] | DEL-CASTILLO-NEGRETE D, CARRERAS B A. Stratified shear flows in a model of turbulence-shear flow interaction[J]. Phys Plasmas, 2002, 9(1): 117-127 |
| [9] | DEL-CASTILLO-NEGRETE D, CARRERAS B A, VIKIE L. Front propagation and segregation in a reaction-diffusion model with cross-diffusion[J]. Physica D, 2002, 168-169(2): 45-60 |
| [10] | BEN ABDALLAH N, DEGOND P, GENIEYS S. An energy-transport model for semiconductors derived from the Boltzmann equation[J]. Journal of Statistical Physics, 1996, 84(1): 205-231 |
| [11] | CHEN L, JÜNGEL A. Analysis of a parabolic cross-diffusion semiconductor model with electron-hole scattering[J]. Communications in Partial Differential Equations, 2007, 32(1): 127-148 DOI:10.1080/03605300601088815 |
| [12] | DEGOND P, GÉNEYS S, JÜNGEL A. A system of parabolic equatinos in nonequilibrium thermodynamics including thermal and electrical effects[J]. Journal De Mathématiques Pures Et Appliqués, 1997, 76(10): 991-1015 DOI:10.1016/S0021-7824(97)89980-1 |
| [13] | SHERRATT J A. Wavefront propagation in a competition equation with a new motility term modelling contact bihibition between cell populations[C]//Proceedings of Mathmatical Physical & Engineering Sciences, 2000, 456(2002): 2365-2386. |
| [14] | GAMBINO G, LOMBARDO M C, SAMMARTINO M. Turing instability and traveling fronts for a nonlinear reaction-diffusion system with cross-diffusion[J]. Mathematics and Computers in Simulation, 2012, 82(6): 1112-1132 DOI:10.1016/j.matcom.2011.11.004 |
| [15] | GAMBINO G, LOMBARDO M C, SAMMARTINO M, et al. Turing pattern formation in the Brusselator system with nonlinear diffusion[J]. Physical Review E, 2013, 88(4): 3250-3270 |
| [16] | GAMBINO G, LOMBARDO M C, SAMMARTINO M. Turing instability and pattern formation in an Activator-Inhibitor system with nonlinear diffusion[J]. Eprint Arxiv, 2014, 132(1): 283-294 |
| [17] | GAMBINO G, LOMBARDO M C, SAMMARTINO M. Turing instability and pattern formation for the Lengyel-Epstein system with nonlinear diffusion[J]. Acta Applicandae Mathematicae, 2014, 132(1): 283-294 DOI:10.1007/s10440-014-9903-2 |
| [18] | DIAMOND P H, LEBEDEV V B, NEWMAN D E, et al. Dynamics of spatiotemporally propagating transport barriers[J]. Phys Plasmas, 1995, 2(10): 3685-3695 DOI:10.1063/1.871068 |
| [19] | WOLLKIND D J, MANORANJAN V S, ZHANG L. Weakly nonlinear stability analysis of prototype reaction-diffusion model equations[J]. Siam Review, 1994, 36(2): 176-214 DOI:10.1137/1036052 |
| [20] | ARANSON I, KRAMER L. The world of the complex Ginzburg-Landau equation[J]. Reviews of Modern Physics, 2001, 74(1): 99-143 |
| [21] | LANDAU L D. On the problem of turbulence[C]//Dokl Akad Nauk SSSR, 1944, 44(8): 339-349. |
| [22] | VAN SAARLOOS W, HOHENBERG P. Fronts, pluses, sources and sinks in generalized complex Ginzburg-Landau equations[J]. Physica D, 1992, 56(4): 303-67 DOI:10.1016/0167-2789(92)90175-M |



