康托尔集[1], 由亨利·约翰·斯蒂芬·史密斯在1875年发现, 并由德国数学家格奥尔格·康托尔在1883年引入.去掉区间中间三分之一的康托尔集(三分康托尔集)是一种最常见, 也最容易构造的分形, 具有很多深刻和显著的性质, 康托尔二元群作为一个超度量空间, 其上定义的小波函数性质良好.因此研究二维康托尔二元群上的小波变换能够更好地解决现实生活中的一些问题.文献[2-4]介绍了沃尔什函数的相关知识.沃尔什变换可以分析信号的频谱, 但是对于非平稳信号具有局限性, 在对信号进行时频分析时不能同时具有时间和频率两方面的局部特性.文献[5-8]概述了一些特殊群上的小波函数和框架, 说明小波理论体系不仅仅只可以用在实数域.文献[9-11]建立了基于康托尔二元群的多分辨率分析的正交小波基.近几年来, 基于康托尔二元集群的小波变换被用于很多领域, 文献[12-16]简述了其在解方程方面的应用.但这些研究都是基于一维康托尔二元群, 因此, 研究基于二维康托尔二元群的小波变换具有深刻意义.选取文献[14]中的Haar小波, 由康托尔集的二维推广联想到二维康托尔二元群, 利用张量积构造出二元尺度函数和小波函数, 建立相应的多分辨分析结构, 并给出实际二维信号的分解与重构算法.
1 二维康托尔二元群 1.1 预备知识∀x∈[0, 1], 可以利用三进制小数对其进行展开, 即
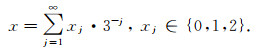
|
记x=(x1x2x3…xn…)为x的三进制展开式, 并作出如下规定, 若

|
则当xk=2时, 取x=(x1x2x3…xk0000000…), xk=1时, 取x=(x1x2x3…xk-10222222…).此时x的三进制表示式唯一.
设E0表示区间[0, 1](其中[a, b]={x|a≤x≤b}), 将E0划分为3个等长的区间, E1表示去掉E0中间的一个开区间后所得到的集合, 则E1包含两个不相交的区间[0, 1/3]和[2/3, 1].将Ek-1划分为3×2k-1个等长的区间, 分别去掉Ek-1中2k-1个区间的中间的开区间的部分得到Ek, 即Ek是由2k个长度为3-k的区间组成.三分康托尔集
设Gk=Ek×Ek, 则Gk中包含了22k个面积为3-2k的矩形.其形成过程如图 1所示.

|
| 图 1 G中的元素(黑色区域) Fig.1 Element in G(The black area) |
从图 1中可以看到, G0中的元素(x, y), x∈[0, 1], y∈[0, 1], 按照康托尔集的构造方法, x, y的取值范围分别去掉中间的1/3, 得到G1.依照此方法继续进行.记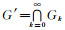
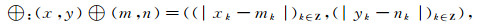
|
其中(x, y), (m, n)∈G.则(G, ⊕)为交换群.二维康托尔二元群与康托尔群具有相似的性质, 因而也可以在此群上建立多分辨分析, 构造相应的尺度函数和小波函数.
2 基于二维康托尔二元群的小波变换文献[14]给出了一维康托尔二元群上的小波函数及其定义.一维康托尔二元群F上的度量为‖·‖:F→[0, +∞), 当x=0时, ‖x‖=0, 否则的话, ‖x‖=2-N(x), 其中N(x)∈ Z, 且满足当xN(x)=1, xk=0, k<N(x).则x和y的距离为

|
x的以2-n为半径的邻域记为

|
为了方便, 简记Ij:=Ij(0), I:=I0(0).F上的函数

|
表明F中的元素与非负实数集是一一对应的.一维康托尔二元群上的扩张函数定义为(ρx)k=xk+1, 则一维康托尔二元群上的尺度函数为ϕ=χI, 其中χI为I上的特征函数, 且ϕj, k可表示为ϕj, k=ϕ(ρj(x)⊕λ-1(k)), j∈ Z, k∈ Z+.由ϕ生成的多分辨分析为

|
相应的小波函数为
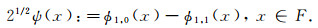
|
一维康托尔二元群上的1周期函数可分解成其上不同分辨率下的尺度函数和小波函数的线性组合, 并能够很好地重构.同理, 在二维康托尔群上也可以建立多分辨分析, 并构造相应的尺度函数和小波函数.
定义1 令Vj2:=Vj⊗Vj, 对Vj2中的元素内积定义为

|
其中g*(x, y)表示g(x, y)的复共轭函数.则Vj2构成一个内积空间.
先给出Vj2中正交函数系的一个结论.
定理1 令φ(x, y)=ϕ(x)ϕ(y), 则φ0, k1, k2=ϕ(x⊕λ-1(k1))ϕ(y⊕λ-1(k2)), k1, k2∈ Z+, 构成一组标准正交函数系.
证明 先证正交性, 有
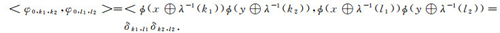
|
再证规范性, 只需证明<φ(x, y), φ(x, y)>=1即可.由于
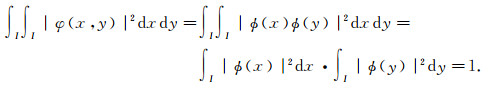
|
因此{φ0, k1, k2}k1∈ Z+, k2∈ Z+是一组标准正交函数系.
接下来, 令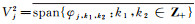
(1) 单调性 …⊂V-22 ⊂V-12 ⊂V02 ⊂V12 ⊂V22 ⊂…⊂Vn2 ⊂…;
(2) 逼近性 
(3) 伸缩性 f(x, y)∈Vj2 ⇔f(ρ(x), ρ(y))∈Vj+12, ∀j∈ Z;
(4) 平移不变性性 f(x, y)∈V02 ⇔f(x⊕λ-1(m), y⊕λ-1(n))∈V02, ∀m, n∈ Z+;
(5) Riesz基存在性 {φ0, k1, k2:k1, k2∈ Z+}构成了V02的Riesz基.
故φ生成了一个多分辨分析(MRA){Vj2}j∈ Z, 其中Vj2:=Vj⊗Vj, 且φ(x, y)∈V02.
该多分辨分析对应的双尺度方程为

|
简记为

|
(1) |
继而可得

|
如下定理2给出了与之相对应的小波函数的表达式.
定理2 令

|
(2) |
则
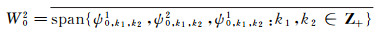
|
构成V02在V12的正交补, 即V12=V02 ⊕W02.且{ψ0, k1, k21, ψ0, k1, k22, ψ0, k1, k21:k1, k2∈ Z+}构成W02的一组标准正交基.
证明 首先证明{ψ0, k1, k21, ψ0, k1, k22, ψ0, k1, k21:k1, k2∈ Z+}是W02的一组标准正交基.先证正交性, 有

|
再证规范性,只需证明

|
因为
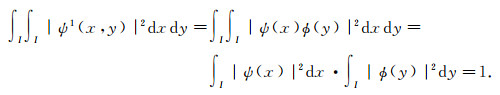
|
同理可证∫I∫I|ψ2(x, y)|2dxdy=1, ∫I∫I|ψ3(x, y)|2dxdy=1.故{ψ0, k1, k21, ψ0, k1, k22, ψ0, k1, k21:k1, k2∈ Z+}是W02的一组标准正交基.
其次, 证明W02构成V02在V12的正交补.由于

|
故V02 ⊥W02.
又因为, 由式(1)~(2)可得2φ1, 0, 0=φ0, 0, 0+ψ0, 0, 01+ψ0, 0, 02+ψ0, 0, 03, 易证对∀f(x, y)∈V12, 有

|
因此V12=V02 ⊕W02.
类似地, 可以证得Vn+12中每一个与Vn2正交的函数均属于Wn2.利用递推的方法, 可以得到
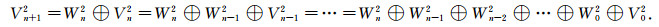
|
因此对于所有的f(x, y)∈L2(G), f都能够表示成

|
由此可以看到, 函数组

|
为相应的小波函数, 并且满足

|
进而可以得到
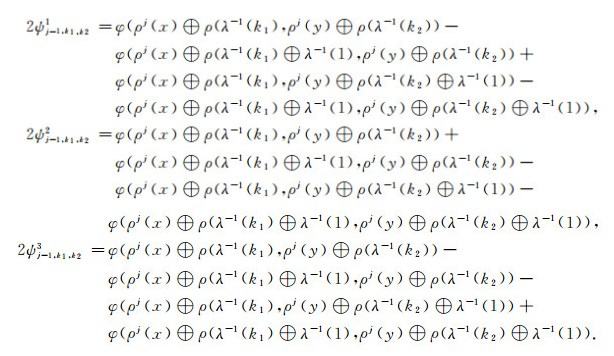
|
则该二维小波函数与尺度函数是正交的.
3 信号的分解与重构算法以上建立了二维康托尔二元组上函数的多分辨分析, 依据上述尺度函数和小波函数对其进行分解和重构.
3.1 信号分解由于MRA的结构, 对所有f(x, y)∈L2(G), 存在一个s, 使得∀ε>0, 有

|
其中fs(x, y)∈Vs2.因此, 只用分解fs(x, y)即可.关于fs(x, y), 有下列分解方式.
定理3 假设

|
则fs(x, y)可以分解为

|
并且

|
满足
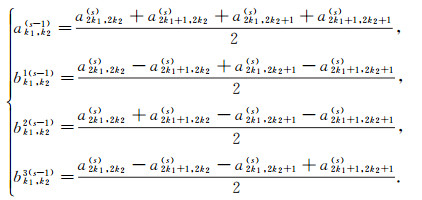
|
上述分解可以一直进行下去, 直到fs=f0+g0+g1+…+gs-1, 其中f0∈V02, gs-1∈Ws-12.
3.2 信号的重构定理4 假设

|
满足

|
则
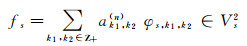
|
的系数可以由下述表达式递推得到:
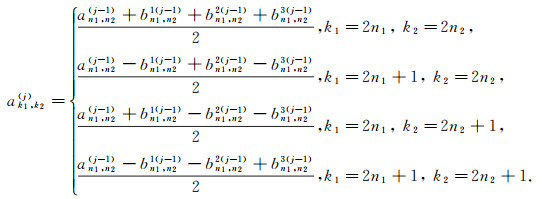
|
其中j=1, 2, 3, …, s.
4 结束语由于小波分析在时域和频域具有表征局部特征的能力, 可以对信号在不同尺度上进行分解与重构, 因此研究分形集上的多分辨分析具有重要的现实意义.文中研究了二维康托尔二元组上的小波变换, 由一维多分辨分析的张量积构造二维可分离多分辨分析, 同理也可以进行更高维的推广和应用.但此种构造方法忽略了两个变量之间的关联性, 为弥补这一缺点, 后续将研究运用瘠波来进行推广.
| [1] |
沙震, 阮火军.
分形与拟合[M]. 杭州: 浙江大学出版社, 2005: 11-15.
SHA Zhen, RUAN Huojun. Fractal and fitting[M]. Hangzhou: Zhejiang University Press, 2005: 11-15. |
| [2] | GOLUBOV B I, EFIMOV A V, SKVORTSOV V A. Walsh series and transforms[J]. Netherlands:Springer, 1991, 91(1): 20-29 |
| [3] | BUTZER P L, WAGNER H J. A calculus for walsh functions defined on R+[J]. Applications of Walsh Functions(Proc Sympos Naval Res Lab), 1973: 76-84 |
| [4] | SHAH F A. Tight wavelet frames generazed by the Walsh polynomials[J]. International Journal of Wavelets, 2013, 11(6): 2797-2813 |
| [5] | YANG Shouzhi, CHENG Zhengxing. Orthonoral multi-wavelets on the interval[0, 1] with multiptiplicity[J]. Acta Mathematica Sinica, 2002, 45(4): 789-796 |
| [6] | FRAKOV Yu A, PROTASOV V Yu. Dyadic wavelets and refinable functions on half-line[J]. Sbornik:Math, 2006, 197(10): 1529-1558 DOI:10.1070/SM2006v197n10ABEH003811 |
| [7] | FARKOV Yu A. Examples of frames on the Cantor dyadic group[J]. Journal of Mathematical Sciences, 2012, 187(1): 22-34 DOI:10.1007/s10958-012-1046-2 |
| [8] | BEZUGLYI S, KWIATKOWSKI J. The topological full group of a Cantor minimal system is dense in the full group[J]. Topol Methods Nonlinear Anal, 2000, 16(2): 371-397 DOI:10.12775/TMNA.2000.046 |
| [9] | LANG W C. Fractal multiwavelets related to the Cantor dyadic group[J]. International Journal of Mathematics, 1998, 21(2): 307-314 |
| [10] | LANG W C. Wavelet analysis on the Cantor dyadic group[J]. Houston Journal of Mathematics, 1998, 24(3): 553-544 |
| [11] | LANG W C. Orthogonal wavelets on the Cantor dyadic group[J]. Siam Journal on Mathematical Analysis, 1996, 27(1): 305-312 DOI:10.1137/S0036141093248049 |
| [12] | BARHARAV Z, LEVIATEN Y. Impedance matrix compression using adaptively contructed basis functions[J]. IEEE Transactions on Antennas & Propagation, 1996, 44(9): 1231-1238 |
| [13] | SU W H, YANG X J, JAFARI H, et al. Fractional complex transform method for wave equations on cantor within local fractional differential operator[J]. Advance in Difference Equations, 2013, 2013(1): 97-105 DOI:10.1186/1687-1847-2013-97 |
| [14] | LEBEDEVA E, SKOPINA M. Walsh and wavelet methods for differential equations on the Cantor group[J]. Journal of Mathematical Analysis and Applications, 2015, 430(2): 593-613 DOI:10.1016/j.jmaa.2015.05.005 |
| [15] | DAI X, HE X, LAI C. Spectral property of cantor measures with consecutive digits[J]. Advance in Mathematics, 2013, 242(1): 187-208 |
| [16] | CHEN J. Fast multilevel augmentation method for nonlinear integral equations[J]. International Journal of Computer Mathematics, 2012, 89(1): 80-89 DOI:10.1080/00207160.2011.627436 |



