2. 榆林学院 数学与统计学院, 陕西 西安 719000;
3. 陇东学院 数学与统计学院, 甘肃 庆阳 745000
2. School of Mathematics and Statistics, Yulin University, Yulin 719000, Shaanxi, China;
3. School of Mathematics and Statistics, Longdong University, Qingyang 745000, Gansu, China
拟阵论[1]是组合数学的一个重要分支, 是一种同时推广了图论和线性代数的数学理论.由于实际的需求和数学工作者的努力, 拟阵理论已经具有比较完善的公理系统, 在组合优化、算法设计、整数规划、信息编码、密码学等领域有广泛的应用.随着模糊集理论[2]的建立以及模糊集思想向许多研究领域的渗透, 模糊拟阵理论的深度研究也相继出现.文献[3-10]定义并系统地研究了模糊拟阵, 通常称为GV模糊拟阵, 它是拟阵与模糊集概念相结合的产物, 史福贵在文献[11]中定义了(L, M)-拟阵, 它是分明拟阵和GV模糊拟阵的一般化, 并且推广了分明拟阵的一些结果.其他学者在此基础上进一步研究了特殊GV模糊拟阵或特殊(L, M)-拟阵的性质[12-20].实际上, 所有这些模糊拟阵都与分明拟阵(简称拟阵或有限拟阵)有很大的联系, 本文将探究这些联系.首先定义拟阵的瘦基运算和弃基并且研究它们的性质, 然后用所得结果刻画正则GV状模糊拟阵.
文中出现的主要记号:
设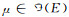
(1) 称μ[r]={x∈E|μ(x)≥r}为模糊集μ的r水平截集.
(2) 称supp μ={x∈E|μ(x)>0}为模糊集μ的支撑集.
(3) 记R+(μ)={μ(x)|x∈supp μ}.
(4) 记m(μ)=infR+(μ), M(μ)=supR+(μ).
(5) 称在点e处取值r(r>0), 在其它点取值0的模糊集Ser为尖.
(6) 用rX表示在X上取值r(r>0), 在其它点取值0的模糊集.
(7) 称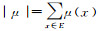
文中将要用到的一些概念:
定义1[1] 设E是一个有限集, 

(I1) ∅∈ 
(I2)若I∈ 

(I3)若I1, I2∈ 

则称



定义2[1] 设E是一个有限集, 若
(B1) 
(B2)若B1, B2∈ 

则称
命题1[1] (1)设E为有限集, 对于每个
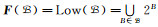




(2) (强交换定理)设B1, B2∈ 


定义3[11, 21] 设E为有限集, L为完全分配格, 若
(LI1) 0E∈
(LI2)若λ∈ 

(LI3)若λ, μ∈ 
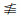

则称

若
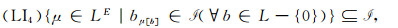
|
则称L-拟阵(E, 
文中约定L={0, 0.5, 1}⊆[0, 1].
命题2[16, 21] (完全L-拟阵的等价条件)设E为有限集,



(*) 对

(ⅰ) μ<λ≤μ∨ν, 其中μ∨ν为μ和μ在(LE, ≤)中的上确界,
(ⅱ) m(λ)≥min{m(μ), m(ν)}.
定义4[22] (正则的L-拟阵)设E为有限集, 








定理1 设(E, 


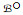


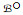
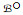
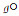
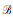

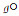

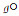
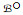
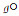

证明 显然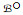
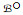

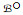


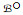
情形1 x2∈B1且x=x2.此时D1-D2=(B1-B2)∪{x2}-{x1}, 因此由|D1-{x}|<|D2|和(I3)知∃y∈D2-(D1-{x})使得(D1-{x})∪{y}∈ 
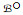
情形2 x2∈B1且x≠x2.此时由D1∪{x1}=B1, D2∪{x2}=B2且x1≠x2, 知x∈B1-B2.因此由

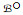
情形3 x2∉B1.此时由D1-D2=B1-B2-{x1}和





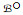



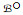
推论1 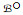

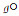

例1 设E={3, 5, 7}, 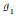
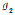
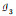
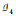
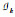
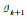
例2 均匀拟阵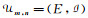

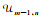
例3 3个顶点的完全图K3的圈拟阵(与例1中的(E, 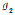
设




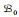
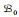



例4 考虑E={3, 5, 7, 9}上的拟阵基系: 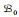

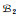
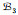
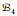
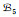
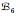
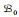
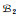
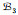

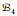
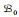
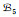
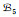
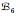
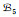
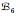

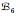
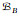
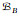
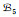
定理2 均匀拟阵基系经过弃基后仍然是拟阵基系.
证明 考虑均匀拟阵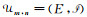



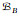

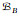
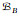

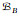

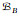


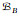
文献[22]给出了构造GV模糊拟阵的一种方法(即用拟阵塔生成GV模糊拟阵), 本节将证明, 每一个正则的GV状模糊拟阵都可以从一个拟阵出发经过拟阵的有限次瘦基运算或弃基而得到.
引理1[1] 设(E, 



引理2[22] 设(E, 
(1) (E, 
(2) 对于每个A∈Max(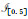
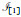
(3) 对于每个ξ∈Max(
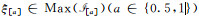
定理3 设
(1) (E, 
(2) 存在E上的拟阵独立集系

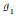

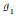

证明 (1)⇒(2).设(E, 

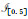
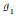
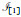
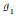


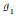

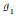


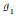

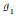



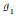
(2) ⇒(1).(E, 

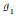









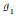

定理4 设
(1) (E, 
(2) 存在E上的拟阵基系





证明 由引理2知(2)⇒(1), 故只须证(1)⇒(2).设(E, 

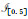

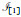





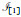
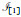
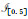
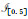

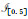
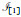

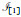






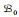
接下来还需证明Max(
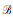






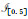

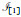








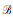

设
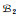

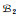

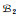
例5 从E={3, 5, 7, 9}上的拟阵基系


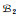
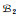
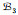



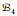
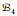
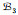
| [1] |
赖虹建.
拟阵论[M]. 北京: 高等教育出版社, 2002: 7-28.
LAI Hongjian. Matroid theory[M]. Beijing: Higher Education Press, 2002: 7-28. |
| [2] | ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353 DOI:10.1016/S0019-9958(65)90241-X |
| [3] | GOETSCHEL R, VOXMAN W. Fuzzy matroids[J]. Fuzzy Sets and Systems, 1988, 27(3): 291-302 DOI:10.1016/0165-0114(88)90055-3 |
| [4] | GOETSCHEL R, VOXMAN W. Bases of fuzzy matroids[J]. Fuzzy Sets and Systems, 1989, 31(2): 253-261 DOI:10.1016/0165-0114(89)90007-9 |
| [5] | GOETSCHEL R, VOXMAN W. Fuzzy circuits[J]. Fuzzy Sets and Systems, 1989, 32(1): 35-43 DOI:10.1016/0165-0114(89)90086-9 |
| [6] | GOETSCHEL R, VOXMAN W. Fuzzy matroids and agreedy algotithm[J]. Fuzzy Sets and Systems, 1990, 37(2): 201-213 DOI:10.1016/0165-0114(90)90043-6 |
| [7] | GOETSCHEL R, VOXMAN W. Fuzzy matroids structures[J]. Fuzzy Sets and Systems, 1990, 41(3): 343-357 |
| [8] | GOETSCHEL R, VOXMAN W. Fuzzy rank functions[J]. Fuzzy Sets and Systems, 1991, 42(2): 245-258 DOI:10.1016/0165-0114(91)90150-O |
| [9] | GOETSCHEL R, VOXMAN W. Spanning properties for fuzzy matroids[J]. Fuzzy Sets and Systems, 1992, 51(3): 313-321 DOI:10.1016/0165-0114(92)90022-V |
| [10] | GOETSCHEL R, VOXMAN W. Fuzzy matroids sum and agreedy algotithm[J]. Fuzzy Sets and Systems, 1992, 52(2): 189-200 DOI:10.1016/0165-0114(92)90049-A |
| [11] | SHI Fugui. (L, M)-fuzzy matroids[J]. Fuzzy Sets and Systems, 2009, 160(16): 2387-2400 DOI:10.1016/j.fss.2009.02.025 |
| [12] |
李小南, 李生刚. 闭模糊拟阵的特征[J].
模糊系统与数学, 2007, 21(4): 48-52 LI Xiaonan, LI Shenggang. The characteristics of closed fuzzy matroid[J]. Fuzzy Systems and Mathematics, 2007, 21(4): 48-52 |
| [13] |
李小南, 李海洋, 李生刚. 模糊拟阵研究[J].
工程数学学报, 2009, 26(3): 431-436 LI Xiaonan, LI Haiyang, LI Shenggang. Research on fuzzy matroid[J]. Journal of Engineering Mathematices, 2009, 26(3): 431-436 |
| [14] | NOVAK L A. On fuzzy independence set systems[J]. Fuzzy Sets and Systems, 1997, 91(3): 365-374 DOI:10.1016/S0165-0114(96)00147-9 |
| [15] | XIN Xiu, SHI Fugui. M-fuzzifying bases[J]. Proyecciones Journal of Mathematics, 2009, 28(3): 271-283 |
| [16] | XIN Xiu, SHI Fugui. Rank functions for closed and perfect[J]. Hacet J Math Stat, 2010, 39(1): 31-39 |
| [17] | XIN Xiu, SHI Fugui, LI Shenggang. M-fuzzifying derived operators and difference derivedo perators[J]. Iranian Journal of Fuzzy Systems, 2010, 7(2): 71-81 |
| [18] | YAO Wei, SHI Fugui. Bases axioms and circuits axioms for fuzzifying matroids[J]. Fuzzy Sets and Systems, 2010, 161(24): 3155-3165 DOI:10.1016/j.fss.2010.07.006 |
| [19] |
李小南, 易黄建, 刘三阳. 模糊拟阵综述[J].
模糊系统与数学, 2013, 27(2): 79-86 LI Xiaonan, YI Huangjian, LIU Sanyang. A survey of fuzzy matroids[J]. Fuzzy Systems and Mathematics, 2013, 27(2): 79-86 |
| [20] |
李小南, 刘三阳, 易黄建. 超拟阵的独立集公理、基公理和圈公理[J].
中国科学:数学, 2016, 46(9): 1351-1364 LI Xiaonan, LIU Sanyang, YI Huangjian. Independent set axioms, base axioms and circuit axioms of supermatroids[J]. Sci Sin Math, 2016, 46(9): 1351-1364 |
| [21] |
张韶煜, 路玲霞, 李生刚, 等. GV状模糊拟阵及其性质[J].
西北大学学报(自然科学版), 2017, 47(2): 157-161 ZHANG Shaoyu, LU Lingxia, LI Shenggang, et al. GV-like fuzzy matroids and their properties[J]. Journal of Northwest University(Natural Science Edition), 2017, 47(2): 157-161 |
| [22] |
赵航, 路玲霞, 李生刚, 等. GV状模糊拟阵的秩与圈[J].
陕西师范大学学报(自然科学版), 2017, 45(3): 6-8 ZHAO Hang, LU Lingxia, LI Shenggang, et al. Ranks and circuits of the GV-like fuzzy matroids[J]. Journal of Shannxi Normal University(Natural Science Edition), 2017, 45(3): 6-8 |



