2. 西安工程大学 理学院, 陕西 西安 710048
2. School of Science, Xi'an Polytechnic University, Xi'an 710048, China
在数值代数中, 由给定的特征值或特征向量构造出相应的矩阵, 称之为特征值反问题或逆特征值问题.特征值反问题在模式识别、数学物理、分子光谱学、结构动力学、自动控制、结构设计及动态分析等领域都有着重要应用[1].而一些具有特殊结构的带状矩阵的特征值反问题, 由于其特殊性和重要应用受到许多学者的关注[2-4].有关三对角矩阵, 包括雅可比矩阵和广义雅可比矩阵的特征值反问题已经取得了许多成果[5-11].五对角矩阵的特征值反问题来自微分方程逆特征值问题的离散化以及结构动力学等领域.文献[12]讨论了由给定的3个特征对构造实对称五对角矩阵的特征值反问题解存在的充分和必要条件, 文献[13]研究了由给定的2个特征对构造实对称五对角矩阵, 给出了解的表达式和数值实验, 文献[14]讨论了由5个不同的特征值和相应的特征向量来构造五对角矩阵的特征值反问题解的存在性的充要条件.而关于非对称的五对角矩阵的特征值反问题研究还较少, 相关结论也不多.文献[15]讨论了由两个互异的特征对构造对角线带有比例关系的五对角矩阵的特征值反问题.以上文献在理论上研究了反问题的存在性和可解性.梁系结构是工程上的重要结构之一, 梁系结构简化为梁模型时, 系统须满足一定的特殊结构, 此时系统的数学实质是一类五对角矩阵.由给定系统的特征值及特征向量来辨识系统的结构参数, 或者反演得到具有实际意义的物理参数, 是解决诸多梁模型结构问题的主要方法.本文主要研究由3个互异的特征对构造非对称五对角矩阵和2个互异的特征对及n-2个实数构造非对称五对角矩阵, 并将所得两类反问题应用于梁系模型中.
1 相关定义与性质定义1[5] 若矩阵
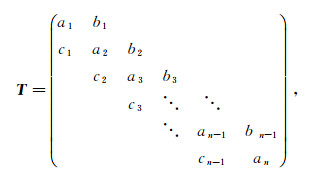
|
(1) |
其中aj(j=1, 2, …, n), bici>0(i=1, 2, …, n-1), aj, bi, ci∈R, 称T为广义雅可比矩阵
定义2 若T中次对角线元素有比例关系, ci=kmbi(k>0, m∈Q, i=1, 2, …, n-1),k是比例系数, 则T可转化为一种基于一定比例关系的不可约三对角矩阵, 记为
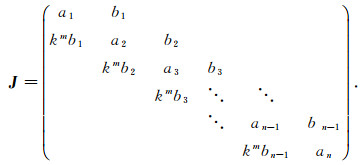
|
(2) |
而五对角矩阵是指如下形状的带状矩阵
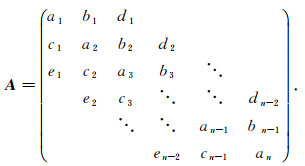
|
(3) |
其中ai(i=1, 2, …, n); bj, cj(j=1, 2, …, n-1);dk, ek(k=1, 2, …, n-2);ai, bj, cj, dk, ek∈R.若ci=kmbi, ej=k2mdj(k>0, m∈Q, i=1, 2, …, n-1, j=1, 2, …, n-2),k是比例系数, 则A可转化为一种基于一定比例关系的五对角矩阵, 记为B.
性质1[6] 两个不可约广义雅可比矩阵的乘积是五对角矩阵.特别的, 如果是两个基于一定比例关系的不可约三对角矩阵J的乘积, 则结果是基于一定比例关系的五对角矩阵B, 即J2= B.
性质2 设(λ, x)是不可约广义雅可比矩阵J的特征对, 则(λ2, x)是五对角矩阵B的特征对.特别地, 若J的所有特征值非负, 且λ是J的第i个特征值, 则λ2是B的第i个特征值.
证明 由定义2, 显然当n≥5时
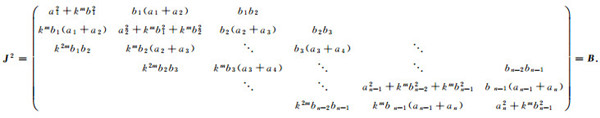
|
(4) |
又设(λ, x)是不可约广义雅可比矩阵J的特征对, 故有Jx=λx.由式(4)得,J2x=Bx=Jλx=λJx=λ2x, 所以Bx=λ2x.又设J的所有特征值非负, 且有λ1<…<λi<…<λn, 则有Jxi=λixi; J2xi=Bxi=λi2xi.所以, 性质2得证.
2 两个非对称五对角矩阵的特征值反问题文中讨论一类特殊的非对称五对角矩阵的特征值反问题, 给出有解的条件及通解的表达式.
问题1 设λ, μ, ν是3个给定的不同实数且有0<λ<μ<ν, x, y, z是3个给定的n维非零实向量, 求一个n阶五对角矩阵B, 使得(λ2, x), (μ2, y), (ν2, z)为B的3个特征对.
问题2 设λ, μ是2个给定的不同实数, x, y是2个给定的n维非零实向量以及给定n-2个实数c1, c2, …, cn-2, 求一个n阶五对角矩阵B, 使得(λ, x), (μ, y)为B的2个特征对, 其中
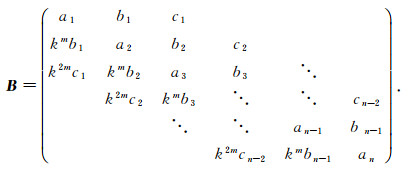
|
(5) |
为便于行文和推导, 给出一些记号.记
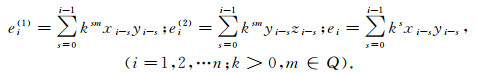
|
(6) |
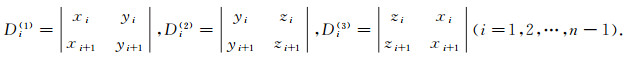
|
(7) |
约定b0=c0=bn=cn=0, b0*=c0*=bn*=cn*=0.
引理1[4] 设λ是不可约广义雅可比矩阵T的特征值, X =(x1, x2, …, xn)T是属于λ的非零实特征向量, 则有:(1) x1xn≠0; (2) xi2+xi+12 ≠0(i=1, 2, …, n).
引理2[6] 设λ, μ是2个给定的不同实数且有λ<μ, X=(x1, x2, …, xn)T, Y =(y1, y2, …, yn)T为2个不同的非零实向量.如果满足以下条件:(1) en=0; (2)Di(1)bi≠0(i=1, 2, …, n-1), ci=kbi(k>0, i=1, 2, …, n-1),k为比例系数.则存在唯一的矩阵J, 使J具有给定的2个特征对(λ, x), (μ, y), 其中主对角线元素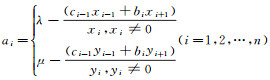
定理1 λ, μ是2个给定的不同实数且有λ<μ, X =(x1, x2, …, xn)T, Y =(y1, y2, …, yn)T为2个不同的非零实向量.如果满足以下条件:(1) en(1)=0; (2)Di(1)bi≠0(i=1, 2, …, n-1); (3) ci=kmbi(k≠0, i=1, 2, …, n-1),k为比例系数.则存在唯一的矩阵J, 使J具有给定的2个特征对(λ, x), (μ, y), 其中主对角线元素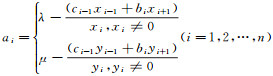
证明 (λ, x), (μ, y)是J的2个特征对, 故有
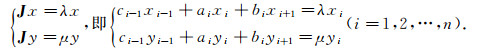
|
(8) |
得
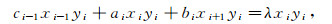
|
(9) |
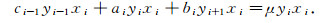
|
(10) |
式(9)与(10)相减得
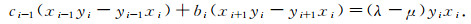
|
(11) |
由条件(3)可知式(11)即为
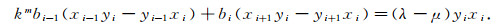
|
(12) |
根据约定的记号以及关系式bi=(μ-λ)ei(1)/Di(1), 式(12)可写成biDi(1)=(μ-λ)ei(1), (i=1, 2, …, n), 由条件(1)得bn=0.由条件(2)得bi=(μ-λ)ei(1)/Di(1) (i=1, 2, …, n-1),相应的ci=kmbi.
将求得的bi, ci代入式(8), 由引理1得
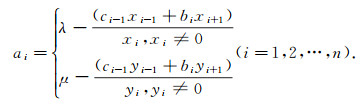
|
定理1得证.
基于上述引理1引理2和定理1的讨论, 下面给出问题1的解,即定理2.
定理2 λ, μ, ν是3个给定的不同实数且有0<λ<μ<ν, X =(x1, x2, …, xn)T, Y =(y1, y2, …, yn)T, Z =(z1, z2, …, zn)T为3个不同的非零实向量, 如果满足以下条件:
(1) en(1)=en(2)=0;
(2) (μ-λ)ei(1)/Di(1)=(ν-μ)ei(2)/Di(2) ≠0(i=1, 2, …, n-1)(yi≠0),
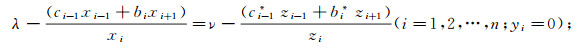
|
(3) ci=kmbi(m∈Q; k>0, i=1, 2, …, n-1), k为比例系数.
则存在唯一的五对角矩阵B, 使B具有给定的3个特征对(λ2, x), (μ2, y), (ν2, z).
证明 条件(1)与条件(2)满足定理1的条件, 那么(λ, x), (μ, y)和(μ, y), (ν, z)可分别确定唯一的矩阵T和T*, 即
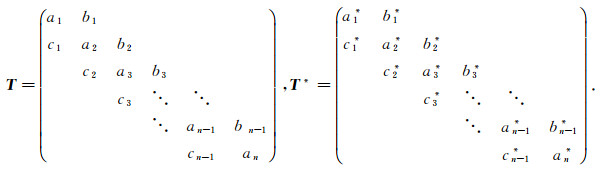
|
(13) |
其中
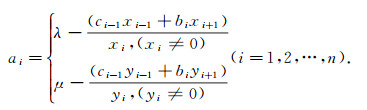
|
(14) |
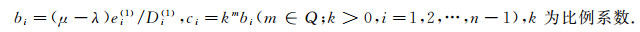
|
(15) |
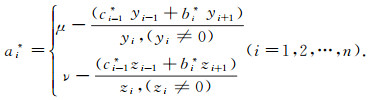
|
(16) |
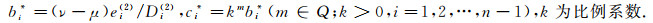
|
(17) |
由条件(2)和(3)可得次对角线元素bi=bi* ≠0;ci=ci* ≠0(i=1, 2, …, n-1).当yi≠0时主对角线元素ai=ai* ≠0(i=1, 2, …, n).当yi=0时, 由条件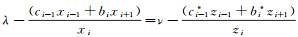
再由性质1与性质2, 可得J2=(J*)2=B, 且(λ2, x), (μ2, y), (ν2, z)为其3个特征对,所以定理2得证.
注 定理2可推广到多个特征对的情形, 若已知k=(4, 5, …, n)个特征对, 问题1可得到类似结果.
下面给出问题2的解,即定理3.
定理3 λ, μ是2个给定的不同实数, x, y是2个给定的n维非零实向量,且给定n-2个实数c1, c2, …, cn-2, 如果满足以下条件:
(1) 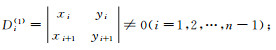
(2) 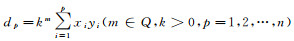
(3) xnyn≠0.
则存在唯一的n阶五对角矩阵B, 使得(λ, x), (μ, y)为B的两个特征对, 其中B同式(5).
证明 (充分性)因为(λ, x), (μ, y)为B的两个特征对, 即有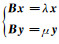
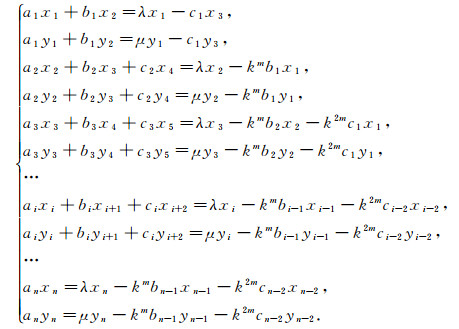
|
(18) |
其中i=3, 4…, n-1.由条件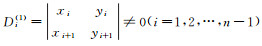
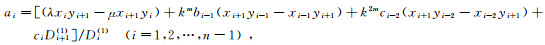
|
(19) |
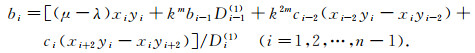
|
(20) |
这里c-1=c0=cn-1=0.
再证anxn=λxn-kmbn-1xn-1-k2mcn-2xn-2与anyn=μyn-kmbn-1yn-1-k2mcn-2yn-2中的an相等.因为
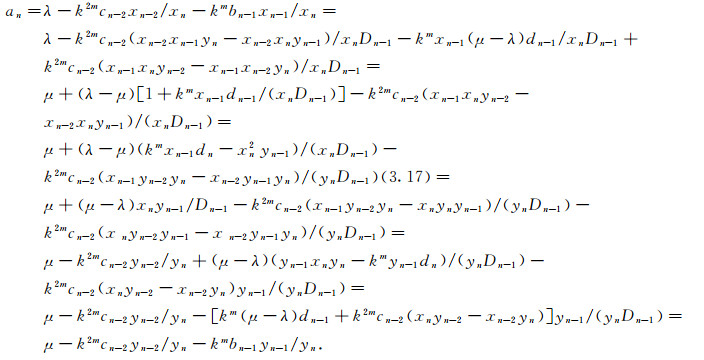
|
所以, 充分性得证.
(必要性)设问题2有解, 即存在唯一的五对角矩阵 B, 使得(λ, x), (μ, y)为B的特征对, 且c1, c2, …, cn-2和k2mc1, k2mc2, …, k2mcn-2是B的次次对角元, 那么方程组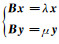
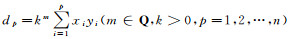
定理3得证, 问题2有唯一解.最后给出定理3的一个推论.
推论1 设λ, μ, ν是3个给定的不同实数, x, y, z是3个给定的n维非零实向量以及给定n-2个实数c1, c2, …, cn-2, 如果满足以下条件:
(1) 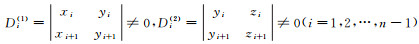
(2) 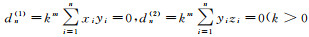
(3) xnynzn≠0;
(4)[(λxiyi+1-μxi+1yi)+kmbi-1(xi+1yi-1-xi-1yi+1)+k2mci-2(xi+1yi-2-xi-2yi+1)+ciDi+1(1)]Di(2)=[(μyizi+1-νyi+1zi)+kmbi-1(yi+1zi-1-yi-1zi+1)+k2mci-2(yi+1zi-2-yi-2zi+1)+ciDi+1(2)]Di(1)且[(μ-λ)xiyi+kmbi-1Di-1(1)+k2mci-2(xi-2yi-xiyi-2)+ci(xi+2yi-xiyi+2)]Di(2)=[(ν-μ)yizi+kmbi-1Di-1(2)+k2mci-2(yi-2zi-yizi-2)+ci(yi+2zi-yizi+2)]Di(1)(i=1, 2, …, n-1).
(5) λ-k2mcn-2xn-2/xn-kmbn-1xn-1/xn=μ-k2mcn-2yn-2/yn-kmbn-1yn-1/yn(i=1, 2, …, n-1).则有唯一的五对角矩阵B,以(λ, x), (μ, y), (ν, z)为3个特征对, B同式(5).其中
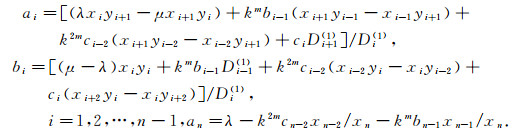
|
证明 由定理3(λ, x), (μ, y)和(μ, y), (ν, z)可分别确定两个唯一的五对角矩阵T和T*, 元素可分别表示为
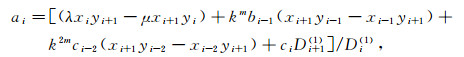
|
(21) |
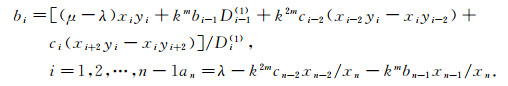
|
(22) |
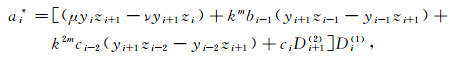
|
(23) |
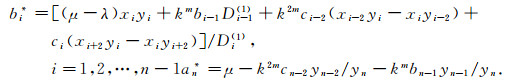
|
(24) |
由条件(4)易得 T = T*, 且以(λ, x), (μ, y), (ν, z)为3个特征对.推论1得证.
3 梁模型应用工程上有很多以梁为主的实际结构被简化为梁模型结构.解决梁模型结构问题的主要方法是由给定系统的特征值及特征向量来辨识系统的结构参数[16-18], 或者反演得到具有实际意义的物理参数.例如方程描述的悬臂梁自由振动系统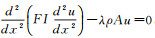
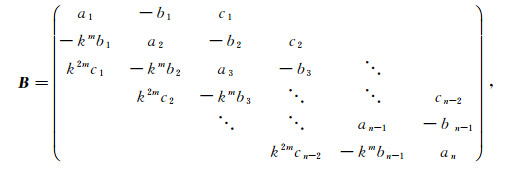
|
其中:
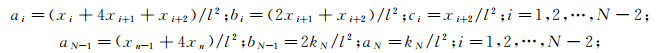
|
算法1 (问题1的解)
输入:实数λ1, λ2, λ3, 3个非零实向量u1=(u11, u12, …, u1n)T, u2=(u21, u22, …, u2n)T, u3=(u31, u32, …, u3n)T, 常数k与m.
输出:五对角矩阵B.
算法2(问题2的解)
输入:实数λ1, λ2, 两个非零实向量u1=(u11, u12, …u1n)T, u2=(u21, u22, …, u2n)T, n-2个实数c1, c2, …, cn-2, 常数k与m.
输出:五对角矩阵B.
例1 取
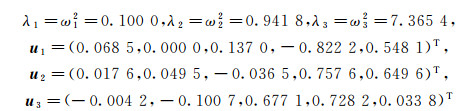
|
为横向位移矩阵.取k=2, m=3, 经验证满足定理2的条件.上机计算可得:
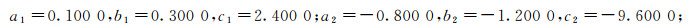
|
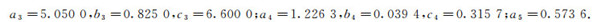
|
存在唯一的矩阵
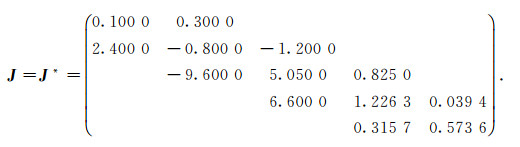
|
得到刚度矩阵

|
例2 取
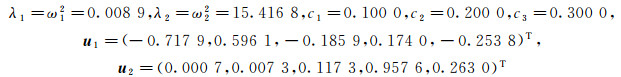
|
为横向位移矩阵.取k=2, m=3.上机计算可得:
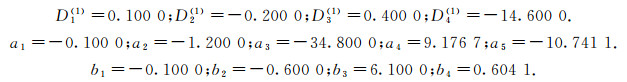
|
得到刚度矩阵

|
文中提出和解决了两类特殊五对角矩阵的特征值反问题, 从理论上证明了问题解的存在性和唯一性, 并得到问题可解的条件和解的表达式.结合工程背景, 探讨这两类特征值反问题在梁系结构模型中的应用, 给出两个数值算法和算例, 数值实验表明结论的正确性和算法的有效性, 为实际工程问题提供了一种解决方法和手段.
| [1] |
哈里曼. 关于矩阵特征值正、反问题的应用背景[J].
新疆大学学报(自然科学版), 1997, 14(4): 26-35 Haliman. The background of matrix's and its inverse eigenvalue problems[J]. Journal of Xinjiang University(Natural Science Edition), 1997, 14(4): 26-35 |
| [2] |
殷庆祥. 实对称带状矩阵特征值反问题的拟Lanczos方法[J].
高等学校计算数学学报, 1989(1): 65-73 YIN Qingxiang. Quasi-lanczos method in solving inverse eigenvalue problem for real symmetric band matrices[J]. Numerical Mathematics A Journal of Chinese Universities, 1989(1): 65-73 |
| [3] |
李杰红. 关于实对称带状矩阵逆特征值问题的广义Lanczos算法[J].
天津科技大学学报, 2011, 26(2): 75-78 LI Jiehong. On the generalized Lanczos algorithm for inverse problem for real symmetric band matrix[J]. Journal of Tianjin University of Science & Technology, 2011, 26(2): 75-78 |
| [4] |
戴华. 实对称矩阵广义特征值反问题[J].
高校应用数学学报, 1992, 7(2): 167-176 DAI Hua. The inverse generalized eigenvalue problem for real symmetric matrices[J]. Applied Mathematies A Journal of Chinese Universities, 1992, 7(2): 167-176 |
| [5] |
戴华. 由谱数据构造周期Jacobi矩阵[J].
高等学校计算数学学报, 1989(3): 261-268 DAI Hua. The construction of periodic Jacobi matrices from special data[J]. Numerical Mathematics A Journal of Chinese Universities, 1989(3): 261-268 |
| [6] |
李志斌, 赵鑫鑫, 李伟. 广义Jacobi矩阵特征值反问题[J].
大连交通大学学报, 2008, 29(4): 6-10 LI Zhibin, ZHAO Xinxin, LI Wei. Inverse eigenvalue problem for generalized Jacobi matrices[J]. Journal of Dalian Jiaotong University, 2008, 29(4): 6-10 |
| [7] |
戴华. Jacobi矩阵和对称三对角矩阵特征值反问题[J].
高等学校计算数学学报, 1990(1): 1-13 DAI Hua. Inverse eigenvalue problems for jacobian and symmetric tridiagonal matrices[J]. Numerical Mathematics A Journal of Chinese Universities, 1990(1): 1-13 |
| [8] |
戴华. Jacobi矩阵特征值反问题[J].
计算物理, 1994, 11(4): 451-456 DAI Hua. Inverse eigenvalue problem for Jacobi matrices[J]. Chinese Journal of Computational Physics, 1994, 11(4): 451-456 |
| [9] |
胡锡炎, 周小庄. 三对角对称矩阵的逆特征问题[J].
数值计算与计算机应用, 1996, 17(2): 150-156 HU Xiyan, ZHOU Xiaozhuang. Inverse eigen problems for tridiagonal symmetric matrices[J]. Journal on Numerical Methods and Computer Applications, 1996, 17(2): 150-156 |
| [10] | BOOR C D. The numerically stable reconstruction of a Jacobi matrix from spectral data[J]. Linear Algebra & its Applications, 1978, 21(3): 245-260 |
| [11] | HOCHSTADT H. On the construction of a Jacobi matrix from mixed given data[J]. Linear Algebra & its Applications, 1979, 28(28): 113-115 |
| [12] |
王正盛. 实对称五对角矩阵逆特征值问题[J].
高等学校计算数学学报, 2002, 24(4): 366-376 WANG Zhengsheng. Inverse eigenvalue problem for real symmetric five-diagonal matrix[J]. Numerical Mathematics A Journal of Chinese Universities, 2002, 24(4): 366-376 |
| [13] |
周小庄, 胡锡炎. 实对称五对角矩阵及其特征反问题[J].
湖南大学学报(自然科学版), 1996, 23(1): 9-14 ZHOU Xiaozhuang, HU Xiyan. The real symmetric five-diagonal matrix and inverse eigenproblems for it[J]. Journal of Hunan University(Natural Sciences), 1996, 23(1): 9-14 |
| [14] |
钱爱林, 吴又胜. 五对角矩阵的特征值反问题[J].
数值计算与计算机应用, 2005, 26(2): 110-117 QIAN Ailin, WU Yousheng. Inverse eigenvalue problem for real symmetric five-diagonal matrix[J]. Journal on Numerical Methods and Computer Applications, 2005, 26(2): 110-117 |
| [15] | TIAN Mingxing, LI Zhibin.Inverse eigenvalue problem for real five-diagonal matrix with proportional relation[C].ICICA 2010:Communications in Computer and Information Science, Tangshan, 2010:48-53. |
| [16] |
王正盛. 特征值反问题的结构探伤方法[J].
振动测试与诊断, 2010, 30(4): 446-450 WANG Zhengsheng. Inverse eigenvalue procedures for damage detection in structure[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4): 446-450 |
| [17] |
王大钧. 结构动力学中的特征值反问题[J].
振动与冲击, 1988(2): 31-43 WANG Dajun. Inverse eigenvalue problem in structural dynamics[J]. Journal of Vibration and Shock, 1988(2): 31-43 |
| [18] | CHAN R H, CHUNG H L, XU S F. The inexact Newton-like method for inverse eigenvalue problem[J]. BIT Numercial Mathematics, 2003, 43: 7-20 DOI:10.1023/A:1023611931016 |
| [19] |
陈新.
机械结构动态设计理论方法及应用[M]. 北京: 机械工业出版社, 1997.
CHEN Xin. The mechanical structure dynamic design theory and application[M]. Beijing: China Machine Press, 1997. |



