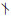 r,p≡1(mod 6);(ⅱ)2
r,p≡1(mod 6);(ⅱ)2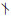 r,p≡5(mod 6),2|s;(ⅲ)2
r,p≡5(mod 6),2|s;(ⅲ)2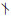 rs,p是Fermat数,则σ(x3)=y2没有正整数解(x,y).
rs,p是Fermat数,则σ(x3)=y2没有正整数解(x,y).
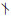 r, p≡1 (mod 6). (ⅱ) 2
r, p≡1 (mod 6). (ⅱ) 2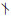 r, p≡5 (mod 6) and 2|s. (ⅲ) 2
r, p≡5 (mod 6) and 2|s. (ⅲ) 2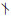 rs, p is a Fermat prime.
rs, p is a Fermat prime.
设Z, N分别是全体整数和正整数的集合.对任意正整数a, 设σ(a)是a的所有约数之和.在初等数论中, 众多有趣的问题都与算术函数σ(a)有关(参见文献[1]). 1657年, Fermat[2]首次研究了方程
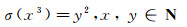
|
(1) |
的解(x, y).Nagell[3]和Ljunggren[4]给出了关于方程
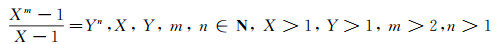
|
(2) |
的两个经典结果, 即如果x是素数方幂, 则方程(1)仅有解(x, y)=(7, 20).此后, 学者们对此方程进行了大量研究, 有关结果可参见文献[5-13].
设p是一个奇素数, r, s是正整数.本文将研究方程(1)的适合

|
(3) |
的解(x, y). 2005年, 乐茂华[14]证明了如果r=s=1, 则方程(1)没有适合方程(3)的解(x, y).最近, 苟素[15]指出了s=1这个条件可从文献[14]的结果中去掉.本文证明了以下一般性的结果.
定理1 当满足下列条件之一时, 方程(1)没有适合方程(3)的解(x, y):
(ⅰ) 2 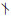
(ⅱ) 2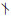
(ⅲ) 2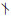
引理1 如果a=p1r1…pkrk是a的素数幂分解, 则
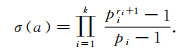
|
证明 参见文献[16]中定理1.9.1.
引理2 对任意的适合2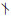
证明 因为2|3r+1, 所以3r+1=2t, 其中t是适合3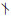
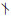
引理3 设D是正整数但非平方数, 则方程

|
(4) |
有解(u, v)且有唯一的使得

|
(5) |
证明 参见文献[16]中定理10.9.1和10.9.2.
引理4 如果方程(4)有适合2|u的一组解(u, v), 则最小解(u1, v1)满足2|u1.
证明 根据引理3可知, (u, v)可表示为式(5).因为2|u, 从式(5)可得2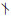
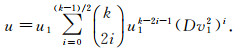
|
(6) |
而且, 由于u12-Dv12=1, 所以u12和Dv12一奇一偶.这表明
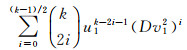
|
是奇数.因此, 从式(6)可知, 2|u1.引理4证完.
引理5 方程

|
仅有解(X, Y, m)=(23, 78, 3)和(13, 239, 4).
3 定理的证明设(x, y)是方程(1)的一组适合方程(3)的解.因为p是奇素数, 根据引理1, 从方程(1)和方程(3)可得
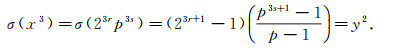
|
(7) |
从式(7)可知
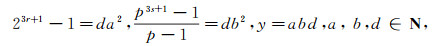
|
(8) |
d是无平方因子.
如果2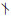

|
(9) |
又因为
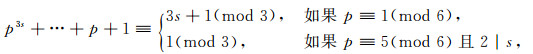
|
(10) |
所以对于情况(ⅰ)和(ⅱ), 式(9)是错误的.这表明方程(1)在这些情况中没有适合(3)的解.
如果2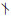
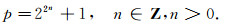
|
(11) |
当n=0时, 从式(11)可知, p=3且式(9)是错误的.故有n≥1.于是从式(8)和式(10)可得, 方程
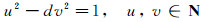
|
(12) |
有两个解, 即
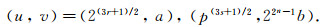
|
(13) |
根据引理4, 从式(13)的第一组解中可知, (u1, v1)满足2|u1.所以, 根据引理3可得, 式(13)的第二组解可表成
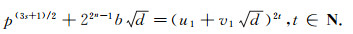
|
(14) |
设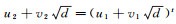

|
(15) |
由文献[15]的结果可知, s≠1, s≥3且(3S+1)/2≥5.但是, 根据引理5可得, 式(15)是错误的.定理1证完.
| [1] | GUY R K. Unsolved problems in number theory[M]. 3rd edition. Beijing: Science Press, 2007. |
| [2] | DICKSON L E. History of the theory of numbers[M]. Washington: Carnegie Institute, 1919. |
| [3] | NEGELL T. Note sur 1'équationée (xn-1)/(x-1)=yq[J]. Norsk Mat Tidsskr, 1920, 2(1): 75-78 |
| [4] | LJUNGGREN W. Noen setninger ou ubestemte likninge av formen (xn-1)/(x-1)=yq[J]. Norsk Mat Tidsskr, 1943, 25(1): 17-20 |
| [5] |
乐茂华. 关于Diophantine方程的一类求解问题[J].
长江大学学报(自然科学版), 2005, 2(7): 185-186 LE Maohua. On the solution of Diophantine equation[J]. Journal of Yangtze University(Natural Science Edition), 2005, 2(7): 185-186 |
| [6] | TERAI N, HIBINO T. On the exponential Diophantine equation (3pm2-1)x+(p(p-3)m2+1)y=(pm)z[J]. Periodica Mathematica Hungarica, 2017, 74(2): 227-234 DOI:10.1007/s10998-016-0162-z |
| [7] |
贾耿华, 周会娟. 有关Fermat数的两个定理[J].
洛阳师范学院学报, 2009, 28(2): 174-175 JIA Genghua, ZHOU Huijuan. Two theorems on Fermat number[J]. Journal of Luoyang Normal University, 2009, 28(2): 174-175 |
| [8] |
曹珍富.
丢番图方程引论[M]. 哈尔滨: 哈尔滨工业大学出版社, 1989.
CAO Zhenfu. Introduction to Diophantine equations[M]. Harbin: Harbin Institute of Technology Press, 1989. |
| [9] |
沈忠华. 有关Fermat数的一个问题[J].
杭州师范学院学报(自然科学版), 2001, 18(4): 21-24 SHEN Zhonghua. On Fermat problem[J]. Journal of Hangzhou Teachers Colledge(Natural Science Edition), 2001, 18(4): 21-24 |
| [10] |
柯召, 孙琦. 关于丢番图方程x4-Dy2=1[J].
数学年刊, 1980, 23(1): 922-926 KE Zhao, SUN Qi. On the Diophantine equation x4-Dy2=1[J]. Chinese Annals of Mathematics, 1980, 23(1): 922-926 |
| [11] |
张四保, 罗霞. 有关Fermat数的一个性质结论[J].
沈阳大学学报(自然科学版), 2007, 19(4): 25-26 ZHANG Sibao, LUO Xia. A property and a conclusion about Fermat number[J]. Journal of Shenyang University(Natural Science Edition), 2007, 19(4): 25-26 |
| [12] | CHEN J H, VOUTIER P M. A complete solution of thediophanantine equation x2+1=dy4 and a related family of quartic Thueequations[J]. Journal of Number Theory, 1997, 62(1): 71-99 DOI:10.1006/jnth.1997.2018 |
| [13] | SPEAR, AM B K. Elliptic curves y2=x3-px of rank two[J]. Journal of Okayama University, 2007, 49(2): 183-184 |
| [14] |
乐茂华. 关于Fermat的一个问题[J].
湖北民族学院学报(自然科学版), 2005, 23(1): 17-20 LE Maohua. On Fermat problem[J]. Journal of Hubei Institute for Nationalities(Natural Science Edition), 2005, 23(1): 17-20 |
| [15] |
苟素. 关于数论函数方程σ(x3)=y2[J].
内蒙古师范大学学报(自然科学汉文版), 2013, 12(4): 387-389 GOU Su. On arithmetic function equation σ(x3)=y2[J]. Journal of Inner Mongolia Normal University(Natural Science Edition), 2013, 12(4): 387-389 |
| [16] |
华罗庚.
数论导引[M]. 北京: 科学出版社, 1979.
HUA Lookeng. Introduction to Number Theory[M]. Beijing: Sciense Press, 1979. |
| [17] | LJUNGGREN W. Uber die Gleichung x4-Dy4=1[J]. Arch Math, 1942, 45(5): 61-70 |
| [18] | BENNELT M A, SKINNER C M. Ternary Diophantine equations via Galois representations and modular forms[J]. Canad J Math, 2004, 56(1): 23-54 DOI:10.4153/CJM-2004-002-2 |


