迭代法是求解大型稀疏方程组Ax =b的一种重要方法, 而迭代格式的收敛性和收敛速度则是关键问题.一般地, 迭代法的收敛性与方程组系数矩阵的性质密切相关, 而对系数矩阵作预条件处理是改善迭代格式收敛性及收敛速度的常用方法.
许多学者针对不同类型的系数矩阵[1-6]提出了一系列预条件迭代方法.文献[7]提出在系数矩阵为非奇异M阵的条件下, 运用USSOR迭代法及矩阵分裂理论, 获得了预条件USSOR迭代法与传统USSOR迭代法谱半径的比较定理.之后文献[8]提出在系数矩阵为H-阵的条件下, 对预条件USSOR迭代法的收敛性进行了修正.文献[9-10]采用特征向量法证明了在线性方程组的系数矩阵为不可约L阵的条件下, 通过满足一定条件, 得到预条件敛散性的比较定理.该方法的优点是预条件迭代法的谱半径严格小于传统迭代法的谱半径.文献[11]则在此基础上提出了一种新的预条件USSOR矩阵, 在系数矩阵为不可约L阵的条件下, 运用特征向量的方法比较了预条件USSOR迭代法和传统USSOR迭代法谱半径的大小, 获得了预条件USSOR的敛散性定理.此后预条件PSD迭代法[12-14]受到众多学者的关注.文献[15]在系数矩阵为不可约L阵的条件下, 使用特征向量的方法比较了预条件PSD迭代法和传统PSD迭代法谱半径的大小关系, 获得了预条件PSD迭代法的敛散性定理.本文在此基础上进行改进, 找到不同的预条件矩阵, 在系数矩阵为没有零元素的L阵的条件下, 使用特征向量的方法比较预条件PSD迭代法和传统PSD迭代法谱半径的大小, 获得新的预条件PSD迭代法的敛散性定理.
1 预备知识定义1[1] 设方阵A =(aij)的阶n≥2, 若对集合W=1, 2, …, n的任意两个非空不相交的子集S和T, S+T=W, 都有i∈S和j∈T满足aij≠0, 则称A不可约, 否则称A可约.
定义2[1] 记所有的n×n实阵A =(ai, j)所组成的集合是Rn, n,Rn, n的子集为

|
当A ∈Zn, n, aii>0(∀i), 称A为L阵.
定义3[1] 如果A ∈Rn, n,A可以表示为A =sI -B,I为n阶单位阵,B为n阶非负矩阵, 当s≥ρ(B)时, 称A为M阵.当s>ρ(B)时, 称A为非奇异M阵.当s=ρ(B)时, 称A为奇异M阵.
定义4[2] 设A为实方阵, 若M为非奇异矩阵, 则称A =M -N是A的一个分裂, 并称这一分裂为
(1) M分裂, 如果M是非奇异M矩阵且N ≥0;
(2) 正规分裂, 如果M-1≥0且N ≥0;
(3) 弱正规分裂, 如果M-1≥0且M-1N ≥0.
定义5[3] 设A =(ai, j)∈Rn×n, 如果存在数λ(实数或复数)和非零向量x, 使得Ax =λx, 其中x =(x1, x2, …, xn)T∈Rn, 则称λ为A的特征值,x为A相对应于λ的特征向量.A的全体特征值称为A的谱, 记作σ(A), σ(A)=λ1, λ2, …, λn.记ρ(A)=max|λi|(1≤i≤n)称为矩阵A的谱半径.
引理1[1] (Perron-Frobenius定理)若A为非负不可约方阵, 则
(1) A有一个正的特征值等于其谱半径ρ(A);
(2) A有与其谱半径ρ(A)相对应正的特征向量;
(3) A的任一元素增加时, ρ(A)也增加;
(4) ρ(A)为A的简单特征值.
引理2[1] 若矩阵A,B为同阶方阵且|B |≤A, 则ρ(B)≤ρ(A).
引理3[4] 若A是一个非负矩阵, 则
(1) 对于某不为0的非负向量x, 若Ax ≥βx, 则ρ(A)≥β;
(2) 对于正向量x, 如果Ax < βx, 则ρ(A)≤B; 如果A为不可约的, 则ρ(A) < β;
(3) 存在向量x >0, 如果βx <Ax <x, 则β < ρ(A) < γ.
引理4[5] 若A为不可约矩阵,A =M -N是A的一个M分裂且N ≠0.则存在向量x >0, 使得M-1N x =ρ(M-1N)x且ρ(M-1N)>0.
2 PSD迭代法的一类预条件考虑线性方程组Ax =b的预条件PSD迭代法.通常情况下, 假设A =I -L -U, 其中A为不可约L阵,I是n阶单位矩阵, -L, -U分别是系数矩阵A的严格下三角矩阵和严格上三角矩阵.预条件方法就是找到一个适当的预条件矩阵P =I +S, 然后将线性方程组表示为新的形式:P Ax=P b, 其中P是非奇异方阵.本文给出了一类预条件矩阵P =I +S, 其中

|
当τ, ω为实数, 且τ≠0时, PSD迭代法的迭代矩阵为
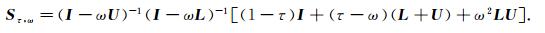
|
给线性方程组作预条件P =I +S后, 记A=(I +S)A,A是线性方程组Ax =b的系数矩阵, 则预条件后的系数矩阵为

|
其中D, L, U是A的对角矩阵, 严格下三角矩阵和严格上三角矩阵.因此, 预条件后的迭代矩阵为

|
A是线性方程组Ax =b的系数矩阵, 作预条件P =I +S, 记A=(I +S)A =D -L -U, 则如下定理成立.
定理1 设A是不可约L阵, 且满足0≤ω≤τ≤1, τ≠0, (I +S)L U-L (D)-1 U ≥0, 0≤α2a12a21+…+αna1nan1 < 1, 0 < γiainani < 1(i=2, 3, …, n-1), 则有下列式子成立:
(1) 如果ρ( Sτ, ω) < 1, 则
(2) 如果ρ( Sτ, ω)=1, 则
(3) 如果ρ( Sτ, ω)>1, 则
证明 A =M -N是不可约L阵, 0≤ω≤τ≤1, τ≠0, 其中


|
由于0≤α2a12a21+…+αna1nan1 < 1, 且0 < γiainani < 1(i=2, 3, …, n-1), 因此(D)-1>0, (I +S)L U -L (D)-1U ≥ 0.其中D =I -DSL, U =L +LSL, U =U +USL+USU-S.DSL,LSL,USL分别为SL的对角矩阵、严格下三角矩阵和严格上三角矩阵.USU为SU的严格上三角矩阵.所以A = D -L -U也是L阵.因为ω≤1, 因此(1-ω)(S +DSL)≥0.令y= Sτ, ωx-λx, H=(1+S)LU -L (D)-1 U, 因此可得

|
已知H ≥0, 另z =[ω2((I +S)L U-L (D)-1 U)+(1-ω)(S +DSL)], 如果A中没有零元素, 则H中第一列元素为零, 其余元素均不为零, 此时如果ω≠0, 则z为非零向量, 因此当ω≠0时, (I -ω(D)-1 U)-1(D -ωL)-1z >0.
此时当λ>1, 由上式有

|
同理可得

|
当ω=0, 上述结论依然成立.
假如A中有零元素, 此结果同文献[15].即z ≥0是第一个元为零的非零向量.即

|
因为0≤ω≤τ≤1, 且A不可约, (D)-1 U的第一行第二个元素非零, 故(I -ω(D)-1 U)-1的第一行至少有两个非零元, 又(D -ω L)-1是一个对角元素非零的下三角矩阵, 因此(I -ω(D)-1U)-1(D -ωL)-1的第一行至少有两个非零元, 所以(I -ω(D)-1 U)-1(D -ω L)-1z >0.
此时当λ>1, 由上式有
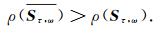
|
同理可得
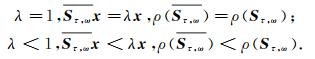
|
当所给线性方程组的系数矩阵A是没有零元素的L阵时, 利用以下3个数值例子来验证前文定理.例1~例3分别验证当λ < 1, λ=1, λ>1的情形, 选取满足条件的参数, 从而验证定理的正确性.
例1 设线性方程组Ax =b的系数矩阵为
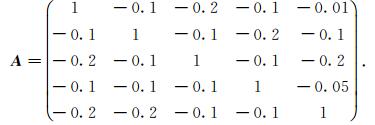
|
取α2=1, α3=0.5, α4=1, α5=4, γ2=1, γ3=1, γ4=0.1, 使用Matlab软件得出预条件P =I +S前后PSD迭代收敛的谱半径ρ(Sτ, ω)和

|
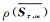
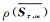
| τ | ω | ρ(Sτ, ω) | 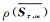 |
τ | ω | ρ(Sτ, ω) | 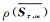 |
|
| 0.3 | 0.1 | 0.837 7 | 0.803 8 | 0.9 | 0.4 | 0.434 8 | 0.341 0 | |
| 0.3 | 0.2 | 0.829 5 | 0.796 3 | 0.7 | 0 | 0.639 3 | 0.558 9 | |
| 0.6 | 0.4 | 0.623 2 | 0.560 6 | 1 | 1 | 0.1691 | 0.094 9 |
从表 1可以看出, 两者的谱半径都小于1, 而预条件PSD迭代法的谱半径
例2 设线性方程组Ax =b的系数矩阵为
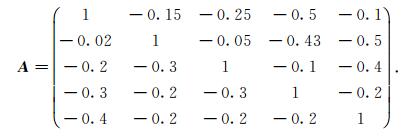
|
取α2=2, α3=1.6, α4=1, α5=1.7, γ2=0.8, γ3=0.75, γ4=1, 使用Matlab软件得出预条件P =I +S前后PSD迭代收敛的谱半径ρ(Sτ, ω)和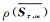

|
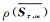
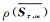
| τ | ω | ρ(Sτ, ω) | 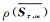 |
τ | ω | ρ(Sτ, ω) | 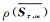 |
|
| 0.3 | 0.1 | 1.000 0 | 1.000 0 | 0.9 | 0.4 | 1.000 0 | 1.000 0 | |
| 0.3 | 0.2 | 1.000 0 | 1.000 0 | 0.7 | 0 | 1.000 0 | 1.000 0 | |
| 0.6 | 0.4 | 1.000 0 | 1.000 0 | 1 | 1 | 1.000 0 | 1.000 0 |
从表 2可以看出, 传统PSD迭代法的谱半径ρ(Sτ, ω)等于预条件PSD迭代法的谱半径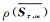
例3 设线性方程组Ax =b的系数矩阵为

|
取α2=2, α3=1.6, α4=1, α5=0.85, γ2=0.8, γ3=0.75, γ4=1, 使用Matlab软件得出预条件P =I +S前后PSD迭代收敛的谱半径ρ(Sτ, ω)和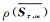
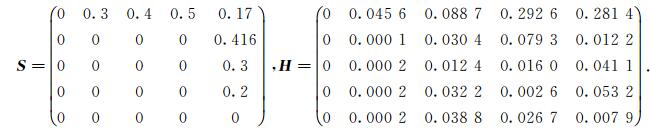
|
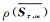
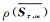
| τ | ω | ρ(Sτ, ω) | 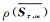 |
τ | ω | ρ(Sτ, ω) | 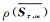 |
|
| 0.3 | 0.1 | 1.015 3 | 1.027 6 | 0.9 | 0.4 | 1.063 5 | 1.1153 | |
| 0.3 | 0.2 | 1.017 1 | 1.030 8 | 0.7 | 0 | 1.032 2 | 1.057 7 | |
| 0.6 | 0.4 | 1.042 3 | 1.076 9 | 1 | 1 | 1.118 0 | 1.216 5 |
从表 3可以看出, 两者的谱半径都大于1, 而预条件PSD迭代法的谱半径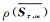
| [1] |
胡家赣.
线性代数方程组的迭代解法[M]. 北京: 科学出版社, 1991.
HU Jiagan. Iterative solution of linear algebraic equations[M]. Beijing: Science Press, 1991. |
| [2] |
唐志强. 线性方程组的预条件广义块AOR, SOR方法[D]. 南京: 南京师范大学, 2002.
TANG Zhiqiang.Preconditioned generalized block AOR and SOR method of linear equations[D]. Nanjing:Nanjing Normal University, 2002. |
| [3] |
李庆阳, 王能超, 易大义.
数值分析[M]. 北京: 清华大学出版社, 2008.
LI Qingyang, WANG Nengchao, YI Dayi. Numerical analysis[M]. Beijing: Tsinghua University Press, 2008. |
| [4] | YOUNG D M. Iterative solution of large linear system[M]. New York: Academic Press, 1971: 142-144. |
| [5] | BERMAN A, PLEMMONS R J, PLEMMONS R J. Nonnegative matrices in the mathematical sciences[M]. Philadelphia: SIAM, 1994. |
| [6] | VARGA R S. Matrix iterative analysis[M]. 2nd edition. Berlin: Springer-Verlag, 2000. |
| [7] |
郭煜, 畅大为. 一类预条件矩阵USSOR迭代方法的比较定理[J].
纺织高校基础科学学报, 2011, 24(4): 546-548 GUO Yu, CHNAG Dawei. Convergence theorems for USSOR iterative method with some preconditioned matrices[J]. Basic Sciences Journal of Textile Universities, 2011, 24(4): 546-548 |
| [8] |
郭煜. 预条件USSOR迭代法存在的问题及修正[J].
纺织高校基础科学学报, 2015, 28(2): 230-233 GUO Yu. Problems and sdution to the preconditioned USSOR iteration method[J]. Basic Sciences Journal of Textile Universities, 2015, 28(2): 230-233 |
| [9] | JAE H Y. Comparison results of the preconditioned AOR methods for L-matrices[J]. Applied Mathematics and Computation, 2011, 218(7): 3399-3413 DOI:10.1016/j.amc.2011.08.085 |
| [10] | JAE H Y. A note on preconditioned AOR method for L-matrices[J]. Journal of Computational and Applied Mathematics, 2008, 220(1): 13-16 |
| [11] |
杨青青, 畅大为, 董瑾. 一类新的预条件USSOR迭代法的比较定理[J].
纺织高校基础科学学报, 2013, 26(4): 507-510 YANG Qingqing, CHANG Dawei, DONG Jin. Comparison theorem of a new preconditioned USSOR iterative method[J]. Basic Sciences Journal of Textile Universities, 2013, 26(4): 507-510 |
| [12] |
林喜梅, 畅大为. PSD迭代方法收敛的充分必要条件[J].
河北大学学报, 2005, 25(6): 571-573 LIN Ximei, CHNAG Dawei. Sufficient and necessary conditions for the convergence of PSD iterative methods[J]. Journal of Hebei University, 2005, 25(6): 571-573 |
| [13] |
柳卫东. PSD迭代法收敛的一个充分条件[J].
纺织高校基础科学学报, 2007, 20(3): 286-288 LIU Weidong. A sufficient condition for the convergence of PSD iterative method[J]. Basic Sciences Journal of Textile Universities, 2007, 20(3): 286-288 |
| [14] |
陈恒新. 关于PSD迭代法收敛的充分必要性定理[J].
应用数学与计算数学学报, 1999, 13(1): 11-20 CHEN Hengxin. The necessary and sufficient theorem for the convergence of PSD iterative method[J]. Communication on Applied Mathematics and Computation, 1999, 13(1): 11-20 |
| [15] |
杨青青. 求解线性方程组预条件PSD迭代法的敛散性分析[D]. 西安: 陕西师范大学, 2014.
YANG Qingqing.Divergence analysis of solving linear equations preconditioned PSD iterative method[D]. Xi'an:Shaanxi Normal University, 2014. |



