2. 陕西师范大学 数学与信息科学学院, 陕西 西安 710119
2. School of Mathematics and Information Science, Shaanxi Normal University, Xi'an 710119, China
“北斗”卫星导航系统是中国自行研制开发的区域性有源三维卫星定位与通信系统, 其民用频点B1I定位精度优于10 m[1].其是美国研发的功能最为完备的卫星导航系统, 其相对定位精度在50 km以内可达10~6 m, 100~500 km可达10~7 m, 1 000 km可达10~9 m. GLONASS是由俄罗斯单独研发部署的卫星导航系统, 其抗干扰性明显强于其他卫星导航系统, 系统单点定位精度水平方向为16 m, 垂直方向为25 m.
“北斗”出生时间尚短, 我国在此领域的技术尚不完善[2-3].国内的研究致力于如何将“北斗”应用于民生与军事中[4-6], 以在各个领域中逐步取代GPS; 通过寻找局部的算法设计来提高“北斗”的定位精确性[7-8]:通过借用GPS、GLONASS或其他成熟的卫星导航系统来改善北斗卫星导航系统的多系统组合等3个方面.目前可实现性较强的组合定位算法有多星座联合、惯性组合、无线定位组合等[1].研究结果表明, 多系统组合在研究中国地区电离层TEC地图、周日变化、逐日变化, 行进式扰动以及电离层的实时监测等方面较单系统具有明显的优势[9].
本文借助“北斗”、GPS和GLONASS对观测点进行组合定位算法设计.首先针对静止观测点的一次定位、静止观测点的多次定位, 提出权重系数组合定位算法.其次, 针对离散型运动观测点定位提出与其相适应的权重系数组合定位算法, 针对连续型运动观测点定位提出了多目标规划组合定位算法, 并将该多目标规划转换为可直接求解的单目标二次规划.该算法即可借助国外先进的卫星定位系统与北斗相结合, 以得到更为精确的定位坐标, 又不依赖于GPS或GLONASS, 在军事应用中具备较强的实用性与保密性.
1 静止观测点在某一定点对同一静止中的观测点分别使用3种卫星导航系统进行定位, 由此可以得到不同的定位坐标, 然后进行组合定位.
1.1 多次定位针对每种卫星导航系统, 对同一观测点都会得到一系列离散的定位坐标.组合定位的思路是留下密集的坐标, 去除离散的坐标.当样本点足够多的时候, 默认是均匀分布在精确坐标的某一邻域内, 即偏离误差可以相互抵消.
假设:最终精确定位坐标为(x, y, z), “北斗”对观测点进行多次定位后所得的一系列的坐标为(xib, yib, zib), 增益误差εb=10 m; 使用GPS所得到的一系列的坐标为(xig, yig, zig), 增益误差εg=10 m; GLONASS得到的一系列的坐标(xil, yil, zil), 其增益误差
以“北斗”为例, 假设定点观测得到的一系列的坐标样本
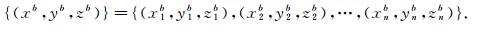
|
剔除离散的点.记(xb0, yb0, zb0)=E((xb, yb, zb)).以(xib, yib, zib)(i=0, 1, 2, …, n)为球心, εb为半径做球Obi, 并计算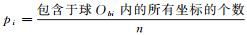
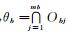
采用如上方法, 得到针对GPS与GLONASS的区域θg, mg和θl, ml.
分别取θb, θg, θl的重心坐标为(xb, yb, zb), (xg, yg, zg), (xl, yl, zl).定位坐标为
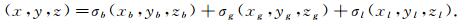
|
其中, 
在定点分别使用3种卫星导航系统对同一观测点进行1次坐标定位, 这样得到3个定位坐标, 然后进行组合定位.
假设 最终精确定位坐标为(x, y, z), “北斗”、GPS和GLONASS所得定位坐标分别为(xb, yb, zb), (xg, yg, zg)和(xg, yg, zg), 若xb=xg=xl, yb=yg=yl, zb=zg=zl, 则(x, y, z)=(xb, yb, zb)=(xg, yg, zg)=(xl, yl, zl).但在实际操作中, 一般得到3个不同点.则
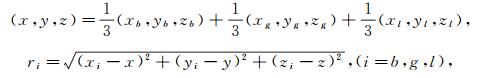
|
若ri≤2εi(i=b, g, l), 则
令
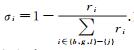
最后, 令
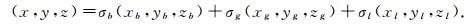
|
当某一卫星导航系统失效或受到较强干扰, 该算法会将其系数为0.
2 动态观测点在实际中, 针对运动中的观测点进行观测时, 一般采用跟踪定位法, 即每隔单位时间分别用3种卫星导航系统对运动中的观测点进行一次坐标定位.
2.1 离散型运动轨迹观测点进行不连续运动, 无法拟合出其运动轨迹方程.这种情况下尽可能多的采集其离散的定位坐标, 即采集坐标的时间间隔尽可能的短, 在三维坐标中绘制出其运动轨迹.
假设最终精确定位坐标为{(xi, yi, zi)| i=1, 2, …, n}; “北斗”、GPS和GLONASS对观测点进行定位后所得的一系列的坐标分别为(xib, yib, zib), (xig, yig, zig), (xil, yil, zil).
针对每一个i=1, 2, …, n, 可视为在定点分别使用3种卫星导航系统对同一观测点进行1次坐标定位.故可以采用1.2中的方法进行组合定位, 这样就可以得到精确定位坐标的点集:{(xi, yi, zi)|i=1, 2, …, n}.
2.2 连续型运动轨迹观测点的运动轨迹为空间内的连续曲线, 这样就可以拟合出其运动轨迹方程.
这种情况下, 处理方法有两种, 一种为先对采集的坐标进行组合定位, 方法同上, 然后用定位后的坐标点曲线拟合运动轨迹方程; 第二种方法为分别对3种卫星导航系统所采集的坐标进行曲线拟合, 得到3条不同的运动轨迹方程, 然后对这3条运动轨迹方程进行组合定位, 得到最终运动轨迹方程.通过大量的实验发现, 两种方法在实际中均是可行的, 第一种方法耗时短、操作难度小, 而第二种方法得到的定位效果更好.所以, 在这里重点介绍第二种组合定位方法.
假设 针对3种卫星导航系统所采集的坐标进行曲线拟合后, “北斗”卫星导航系统得到的观测点的运动轨迹方程为
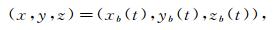
|
(1) |
其中, t表示时间.GPS得到的观测点的运动轨迹方程:

|
(2) |
GLONASS得到的观测点的运动轨迹方程:
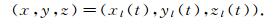
|
(3) |
最终误差修正后的运动轨迹方程:
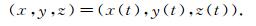
|
(4) |
若3种卫星导航系统在第t1, t2, …, tn时刻得到的定位坐标一致, 将其依次记为(xi, yi, zi)i=1, 2, …, n, 则式(4) 过点(xi, yi, zi)i=1, 2, …, n.
本文默认为每种卫星导航系统得到的运动轨迹方程都没有偏离其增益误差.要求得的运动轨迹方程(4) 在同一时刻应该尽可能的同时接近于另外3条已知的运动轨迹方程.并且, 在任一个时刻t通过式(4) 得到的坐标(x(t), y(t), z(t)), 应该同时位于下述3个球内:
球Ob(t):以(xb(t), yb(t), zb(t))为球心, εb为半径的球;
球Og(t):以(xg(t), yg(t), zg(t))为球心, εg为半径的球;
球Ol(t):以(xl(t), yl(t), zl(t))为球心, εl为半径的球.
由上述分析, 可得如下多目标规划数学模型:
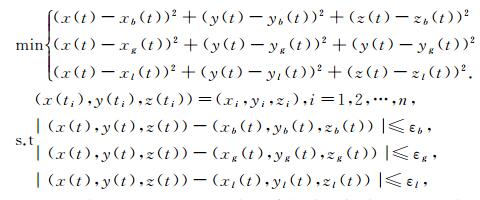
|
(5) |
如上多目标规划的解即为式(4).现在国际上流行的求解多目标线性规划的方法, 最简单有效的求解方法是化多目标为单目标, 再根据转化后模型特点进行求解.本文采用加模的转换方法.
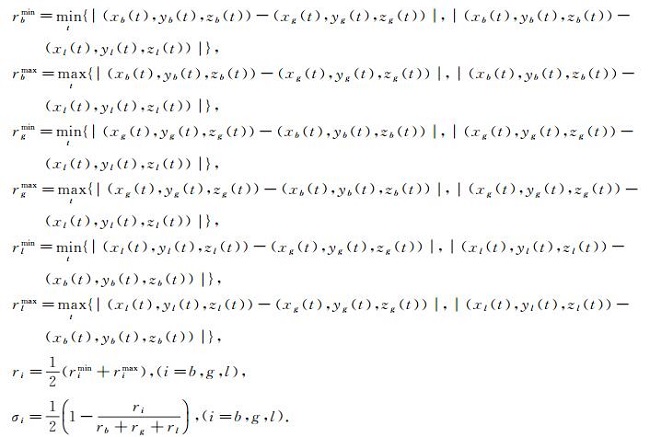
|
则目标函数转化为单目标二项式规划:
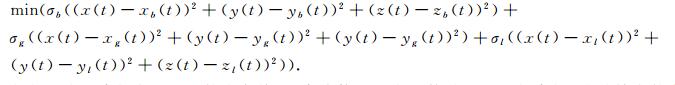
|
(6) |
这种工程规划现在的求解方法已经较为完善, 可直接使用现有的数学工具进行求解, 收敛精度较高.采用二项式规划求解方法与线性规划求解算法, 得到最后的所求运动轨迹方程式(4).
3 结论(1) 针对静止观测点的1次定位、静止观测点的多次定位、离散型运动观测点、连续型运动观测点等4种情况分别提出了与其相适应的组合定位算法:权重组合定位算法与多目标规划组合定位算法.
(2) 所提出的算法是借助于“北斗”、GPS和GLONASS进行组合定位, 但又不依赖于GPS和GLONASS, 在军事应用中具有较强的实用性与保密性.
(3) 在实际使用多目标规划组合定位算法时, 将其转化为可直接求解的单目标二次规划.
| [1] |
韩逸飞. 北斗组合定位技术概论[J].
电子技术应用, 2013, 12: 9-11 HAN Yifei. Overview of Beidou integrated positioning technology[J]. Application of Electronic Technique, 2013, 12: 9-11 DOI:10.3969/j.issn.0258-7998.2013.02.002 |
| [2] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J].
测绘学报, 2010, 39(1): 1-6 YANG Yuanxi. Progress, contribution and challenges of compass/Beidou satellite navigation system[J]. Acta Geodaeticaet Cartographica Sinica, 2010, 39(1): 1-6 |
| [3] |
许其凤. 认识北斗建设北斗[J].
中国工程科学, 2014(8): 26-32 XU Qifeng. Understand and construct Beidou navigation system[J]. Engineering Sciences, 2014(8): 26-32 |
| [4] |
陈炜峰, 薛冬, 周旺平. 北斗导航辅助移动机器人同时定位和地图构建研究[J].
科学技术与工程, 2014, 19: 91-94 CHEN Weifeng, XUE Dong, ZHOU Wangping. The simultaneous localization and map building integrated compass navigation of mobile robot[J]. Science Technology and Engineering, 2014, 19: 91-94 DOI:10.3969/j.issn.1671-1815.2014.11.019 |
| [5] |
张颖, 王钤, 兰光武, 等. 北斗/INS组合导航在某型装备中的应用设计[J].
设计兵工自动化, 2014, 12: 41-45 ZHANG Ying, WANG Qian, LAN Guangwu, et al. Application and design of Beidou/INS integrated navigation system in certain type weaponry equipment[J]. Ordnance Industry Automation, 2014, 12: 41-45 |
| [6] |
吴斌, 蒋和松, 郭明明, 等. 基于北斗卫星导航的车辆监控系统[J].
电子测试, 2014, 24: 84-86 WU Bin, JIANG Hesong, GUO Mingming, et al. Design of vehicle monitoring system based on Beidou navigation satellite system[J]. Electronic Test, 2014, 24: 84-86 DOI:10.3969/j.issn.1000-8519.2014.18.035 |
| [7] |
谢小刚, 曾大治, 龙腾, 等. 北斗GEO卫星广播星历的直接拟合算法研究[J].
华中科技大学学报(自然科学版), 2014(3): 14-18 XIE Xiaogang, ZENG Dazhi, LONG Teng, et al. Research on broadcast ephemeris direct fitting algorithm of Beidou GEO satellite[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014(3): 14-18 |
| [8] |
张清华, 隋立芬, 贾小林, 等. 北斗卫星导航系统空间信号误差统计分析[J].
武汉大学学报(信息科学版), 2014(3): 271-274 ZHANG Qinghua, SUI Lifen, JIA Xiaolin, et al. SIS error statistical analysis of Beidou satellite navigation system[J]. Geomatics and Information Science of Wuhan University, 2014(3): 271-274 |
| [9] |
熊波, 万卫星, 宁百齐, 等. 基于北斗、GLONASS和GPS系统的中低纬电离层特性联合探测[J].
地球物理学报, 2014, 57(11): 3586-3599 XIONG Bo, WAN Weixing, NING Baiqi, et al. Investigation of mid-and low-latitude ionssphere based on BDS, GLONASS and GPS observations[J]. Chinese Journal of Geophysics, 2014, 57(11): 3586-3599 DOI:10.6038/cjg20141112 |
| [10] |
吴甜甜, 张云, 刘永明, 等. 北斗/GPS组合定位方法[J].
遥感学报, 2014, 57(11): 3586-3599 WU Tiantian, ZHANG Yun, LIU Yongming, et al. Beidou/GPS combination position methodology[J]. Journal of Remote Sensing, 2014, 57(11): 3586-3599 |
| [11] |
刘睿, 张可村. 模糊多目标半定规划的最优性条件[J].
模糊系统与数学, 2009(3): 133-138 LIU Rui, ZHANG Kecun. Optimality condition for fuzzy multi-objective semi-definite programming[J]. Fuzzy System and Mathematics, 2009(3): 133-138 |
| [12] | LIU Rui, ZHANG Kecun. Fuzzy multi-objective semi-definite programming[J]. Journal of Mathematical Research and Exposition, 2010(4): 599-609 |
| [13] | XIONG Bo, WAN Weixing X, NING Baiqi, et al. A statistic study of ionospheric solar flare activity indicator[J]. Space Weather, 2014, 12(1): 29-40 DOI:10.1002/2013SW001000 |
| [14] | WLELGOSZ P, BRZELNSKA Grejner D, KASHANI I. Reglonal ionosphere mapping with kriging and multiquaddric methods[J]. Journal of Global Positioning Systems, 2003, 2(1): 48-55 DOI:10.5081/jgps |
| [15] | PAJARES H M, JUAN J M, SANZ J, et al. The ionosphere:Effects, GPS modeling and the benefits for space geodetic techniques[J]. J.Geod, 2011, 85(11): 887-907 |



