内点算法最初是由Karmarka[1]于1984年为求解线性规划而提出的, 是求解互补问题的一类十分有效的算法.此后许多学者开始关注内点算法及其复杂度的研究.内点算法针对邻域的不同, 分为长步算法和小步算法.Monteiro[2-3]和Kojima[4]等研究了窄邻域小步算法及其复杂度, 叶荫予等[5]提出了一个单调线性互补问题的预估矫正内点算法, 得到窄邻域小步算法的最好的复杂性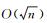
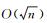
一直以来, 学者们设计的宽邻域算法大多是基于负无穷邻域的, 直到艾文宝等[16]定义了一个新的宽邻域, 并利用该宽邻域首次得到了和窄邻域小步算法复杂性等同的宽邻域长步内点算法, 且具有良好的计算效果.文献[17]将艾文宝邻域进行简化, 给出对称锥优化问题的不可行宽邻域长步内点算法, 也取得了一些较好的理论结果.本文基于文献[17]提出的宽邻域, 对求解单调非线性互补问题的长步齐次算法进行复杂度分析, 得出其理论复杂度与文献[9]的小步算法的理论复杂度相同.
1 齐次模型及齐次算法描述单调非线性互补问题:求(y, z)∈ Rn× Rn, 使得

|
(1) |
其中f(x)是可微的单调非线性映射且满足的假设条件:
假设1 (Scaled Lipschitz Condition)存在单调递增函数v:(0, 1)→(1, ∞), 使得
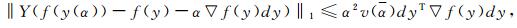
|
这里dy∈ Rn, y∈ R+n满足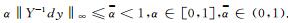
考虑非线性互补问题(1) 的齐次模型(MCP):求(y, τ; z, κ)∈ Rn+1× Rn+1, 使得
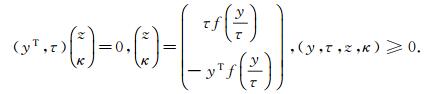
|
(2) |
令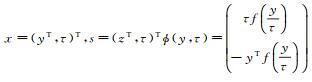

|
(3) |
由文献[4]知, Φ(x)的雅可比矩阵▽Φ(x)是半正定的, 且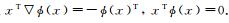
本文考虑下面的宽邻域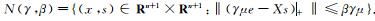
给定初始点(x0, s0)∈N(γ, β), 允许误差ε>0, 令k=0.
步骤1 如果(xk)Tsk≤ε, 则停止.
步骤2 解下列方程组求解方向(dxk, dsk)
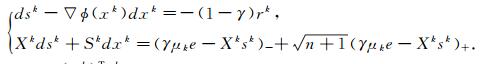
|
(4) |
其中
步骤3 更新的迭代点及互补间隙

|
这里步长αk∈[0, 1]的选择满足下列条件:

|
步骤4 令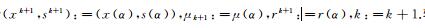
通过简单的计算可以得到下面的表达:
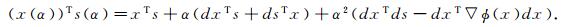
|
(5) |
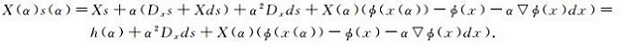
|
(6) |
这里h(α)=Xs+α(Dxs+Xds), Dx=diag(dx)).则
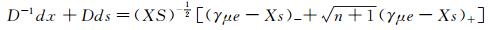
|
(7) |
这里
引理1[9] 若假设1满足, 则存在函数v:(0, 1)→(1, ∞)使得函数Φ满足
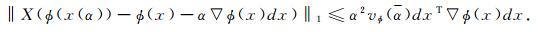
|
这里
引理2 方向(dx, ds)满足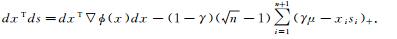
证明 在式(4) 的第一个方程两边分别同乘以dxT和(xk)T有

|
(8) |
又因为-xT▽Φ(x)=Φ(x)T, 故有
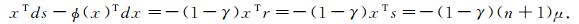
|
(9) |
联合式(8),(9) 有
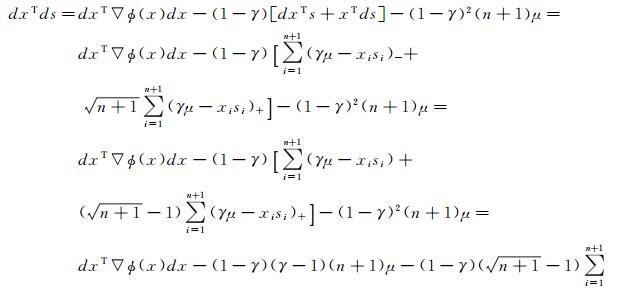
|
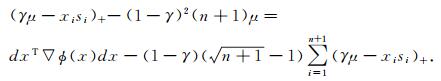
|
引理3 假设r(α), x(α), s(α), μ(α)由步骤3给定, 则有以下结论成立.
(1) r(α)=(1-α(1-γ))r.
(2) (x(α))Ts(α)≥(1-α(1-γ))xTs.
(3) μ(α)≤μ[1+(βγ+(γ-1))α].
证明 由步骤4易得引理3中(1) 的结论, 下面来证明(2).
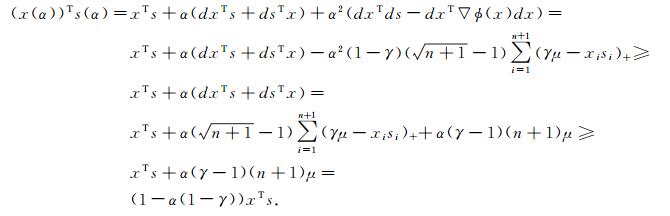
|
因为

|
即μ(α)≤μ[1+(βγ+(γ-1))α].
引理4[17] 当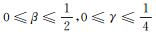

|
引理5 令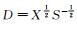
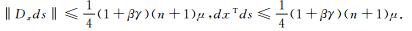
证明 由式(7) 及引理4易得结论成立.
引理6 当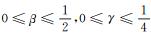
证明 由引理3可知
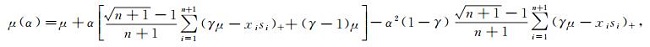
|
所以

|
当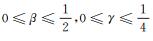
引理7[17] 令μ(α)>0, 则∀α∈[0, 1]有
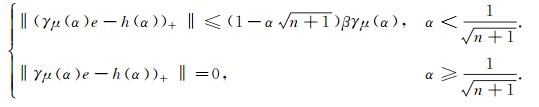
|
为了给出步长α的下界, 定义函数

|
由于μ(α)为严格单减函数, ▽Φ(x)为半正定的即dxT▽Φ(x)dx≥0, 故g(α)在α∈[0, 1]上单调递增.
令αc:=max{α:g(α)≤0, ∀∈[0, 1]}, 故∀α∈[0, αc]都有

|
引理8 ∀α∈[0, αc), 均有‖(γμ(α)e-X(α)s(α))+‖≤βγμ(α).
证明 类似文献[17]中引理5.9.
引理9 令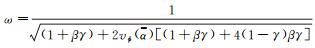
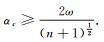
证明 若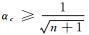
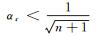
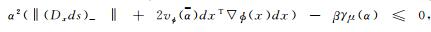
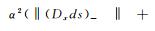

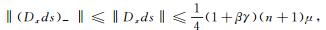
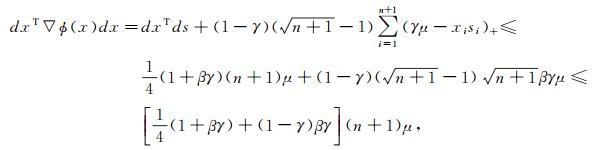
|
故有
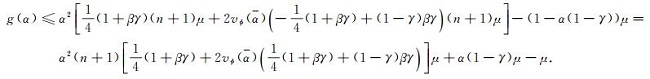
|
类似文献[17]中的方法, 易知当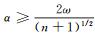
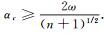
从以上引理1~9可知, 满足步骤3的最大步长
定理1 令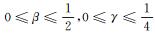
证明 取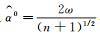
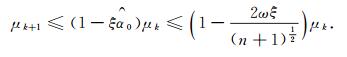
|
显然当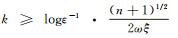
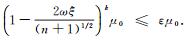
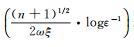
利用2个算例对本文中的宽邻域长步算法与文献[9]的窄邻域小步算法进行比较.这2个算例均为凸优化问题, 其KKT条件即为单调互补问题, 具体问题的转化及其次模型的建立详见文献[9].算法利用Matlab R2014a编程, 在CPU 2.0GHz, RAM 2GB的PC机上执行.这里gap表示对偶间隙, iter表示算法迭代的次数, t表示算法运行的时间, s, 误差ε=10-6.
例1 求解线性约束的凸规划问题min -logx1-logx2.s.t x1+2x2=1, x1≥0, x2≥0.
例2 求解如下凸二次规划问题min q(x)=2x12+3x22+5x32+2x2-3x3.s.t x1+x2=5, x2+x3=10, x1≥0, x2≥0, x3≥0.
计算结果见表 1和表 2.从数据结果可以看出, 本文提出的宽邻域长步算法不仅在理论上获得较好的结果, 而且在实际计算上也有较好的效果.
提出一种针对单调非线性互补问题的宽邻域长步齐次内点算法, 并且估计了该算法的理论复杂度.该宽邻域长步算法的理论复杂度为
| [1] | KARMARKAR N. A new polynomial-time algorithm for linear programming[J]. Combinatorica, 1984, 4(4): 373-395 DOI:10.1007/BF02579150 |
| [2] | MONTEIRO R D C, ADLER I. Interior path following primal-dual algorithms, Part Ⅰ:Linear programming[J]. Math Program, 1989, 44: 27-41 DOI:10.1007/BF01587075 |
| [3] | MONTEIRO R D C, ADLER I. Interior path-following primal-dual algorithms, Part Ⅱ:Convex quadratic programming[J]. Math Program, 1989, 44: 43-66 DOI:10.1007/BF01587076 |
| [4] | KOJIMA M, MIZUNO S, YOSHISE A. A polynomial-time algorithm for a class of linear complementarity problems[J]. Math Program, 1989, 44(1-3): 1-26 DOI:10.1007/BF01587074 |
| [5] | YE Y, ANSTREICHER K. On quadratric and O(n) convergence of a predictor corrector algorithm for LCP[J]. Math Program, 1993, 62(3): 537-551 |
| [6] | GONZAGA C. The largest step path following algorithm for monotone linear complementarity problems[J]. Math Program, 1997, 76(2): 309-332 DOI:10.1007/BF02614443 |
| [7] | KOJIMA M, MIZUNO S, YOSHISE A.A primal-dual interior point algorithm for linear programming[M]//Progress in Mathematical Programming.New York:Springer, 1989:29-47. |
| [8] | GULEAR O. Existence of interior points and interior paths in nonlinear monotone complemntarity problems[J]. Math Oper Res, 2011, 214(3): 473-484 DOI:10.1016/j.ejor.2011.02.022 |
| [9] | ANDERSEN E, YE Y. On a homogeneous algorithm for the monotone complementarity problems[J]. Math Program, 1999, 84(2): 375-400 DOI:10.1007/s101070050027 |
| [10] | SUN J, ZHAO G Y. A quadratically convergent polynomial long-step algorithm for a class of nonlinear monotone complementarity problems[J]. Opyim Methods Softwear, 2000, 48(4): 453-475 |
| [11] | YOSHISE A. Interior point trajectories and a homogeneous model for nonlinear complementarity problem over symmetric cones[J]. SIAM J Optim, 2006, 17(4): 1129-1153 |
| [12] | YOSHISE A. homogenous algorithms for monotone complementarity problems over symmetric cones[J]. Pac J Optim, 2008, 5(2): 313-337 |
| [13] | ZHAO Y B, LI D. A new path-following algorithm for nonlinear P*(k) complementarity problems[J]. Comput Optim Appl, 2005, 34(2): 183-214 |
| [14] | GULEAR O. Existence of interior points and interior paths in nonlinear monotone complemntarity problems[J]. Math Oper Res, 2011, 214(3): 473-484 DOI:10.1016/j.ejor.2011.02.022 |
| [15] | TSENG P. An infeasible path-following method for monotone complementarity problems[J]. SIAM J Optim, 1997, 7(2): 386-402 DOI:10.1137/S105262349427409X |
| [16] | AI W B, ZHANG S Z. An iteration primal-dual path-following method, based on wide neighborhoods and large updates, for monotone LCP[J]. SIAM J Optim, 2005, 16(2): 400-417 DOI:10.1137/040604492 |
| [17] | LIU H, YANG X, LIU C. A new wide neighborhood primal-dual infeasible-interior-point method for symmetric cone programming[J]. J Optim Theory Appl, 2013, 158(3): 796-815 DOI:10.1007/s10957-013-0303-y |



