在宏观经济研究中, 国家或政府往往会有计划地制定一系列政策目标, 主要包括充分就业、经济增长、物价稳定和国际收支平衡四个方面.其中物价稳定对经济平稳运行具有关键性的作用.消费者价格指数(CPI)和生产者价格指数(PPI)是衡量物价水平的两大重要指标, 故有一系列文献对两者之间的相关性问题进行了研究分析[1-4].但是大多是在线性模型基础上提出的.而线性相关系数对于非正态分布的随机变量并不一定适用, 于是便引入了Copula函数.Copula函数最早是由国外统计学家Sklar提出的[5]. 1998年, Nelsen[6]系统地讨论了Copula函数的定义、相关性等一系列问题, 随后Copula函数开始应用到金融领域.文献[7-9]系统地介绍了Copula理论, 并将Copula函数应用到了股票市场, 对各股票指数进行了相关性分析.文献[10]对各相关性系数指标进行了讨论, 并以沪深日收盘综合指数为例, 在一个Copula族内适当变换, 最终得到一个较好的模型并进一步讨论了沪深指数的相关性.文献[11]利用Copula函数进行线性组合得到混合Copula, 并应用其对金融现象进行了模拟.然而, 大多数的研究只局限于股票证券领域.2010年起, Copula函数开始被应用于CPI与PPI等宏观指标的相关性分析.文献[12]分析了CPI与PPI的运行状况, 并首先提出用Copula函数进行拟合, 最终用后验检验来得到相关结论.文献[13]对CPI与PPI的相互关系做了实证分析, 通过平方欧式距离检验, 得到t-Copula是所有Copula函数中对CPI和PPI的拟合程度最优的结论.但以上研究均为用单个Copula对CPI、PPI进行拟合分析, 本文构建混合Copula模型来进行多变量相关性分析.针对CPI与PPI非线性非对称性的特点, 采用非参数核密度估计的方法建立CPI与PPI的边缘分布函数, 选择混合Copula函数建立多个变量之间的相关结构, 有效地克服了单一Copula函数所带来的不足, 最终得到具有更好的拟合效果的模型.
1 Copula函数基本理论 1.1 二元Copula基本理论定义1[6] 若一个二维函数C(u, v)满足下列条件:
(1) C的定义域是S1×S2, 其中S1, S2分别是[0, 1]的子集.
(2) C是有基面的,而且是二维单调递增的.
(3) 对于任意的u, v分别属于S1, S2, 均满足C(u, 1)=u, C(1, v)=v.
则称该二维函数为Copula函数.其中称二元函数H(x, y)有基面,若在S1, S2中存在最小的点a1, a2, 使得H(a1, y)=H(x, a2)=0.
性质1[6] 设C(u, v)为Copula函数, 则
(1) C(u, 0)=0=C(0, v).
(2) 若C(u, v)的二阶偏导存在, 则有C(u, v)=Ac(u, v)+Sc(u, v), 其中

|
若Sc=0, 则C绝对连续.
若C(u, v)绝对连续, 令u=F(x), v=G(y),则得到(X, Y)的联合密度函数为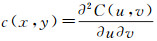
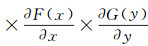
(3) 若C1(u, v), C2(u, v), …, Ck(u, v)为k个不同的Copula函数, 则其凸线性组合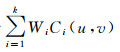
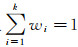
在金融分析中, 大量的数据都存在着尖峰厚尾[14]的情况.而在这种现象下, 研究变量之间的尾部相关性[15]是很有意义的.而Copula函数的出现, 为尾部相关性的度量提供了极大的便利.变量之间的尾部相关是指当随机变量X大幅增加或大幅减少时, 随机变量Y也大幅增加或减少的概率.引入到本文中即可以表示当PPI出现较大波动时, 是否会引起CPI的较大波动, 用于研究CPI和PPI间的相互影响.在Copula函数中, 上尾相关系数和下尾相关系数表达式为
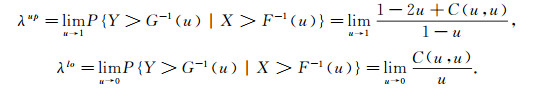
|
若λup(或λlo)存在且在区间(0, 1], 则称随机变量X, Y上尾(或下尾)相关.当随机变量独立时, λup=λlo=0.
2 混合Copula模型的构造Copula函数的种类很多, 不同的Copula函数有不同的特征.其中阿基米德Copula函数性质优良, 在描述金融数据中最为常用, 因此本文应用以下三种常用的阿基米德Copula函数[6]来构造混合Copula模型.
(1) Gumbal Copula函数
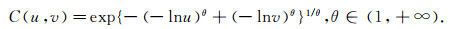
|
Gumbal Copula函数对变量在分布上尾部的变化十分敏感.若随机变量用Gumbal Copula来拟合更为合适, 说明此分布在上尾部变量间具有更强的相关性.
(2) Clayton Copula函数

|
Clayton Copula函数对变量在下尾部的变化十分敏感.若随机变量用Clayton Copula来拟合更为合适, 说明此分布在下尾部变量间具有更好的相关性.
(3) Frank Copula函数
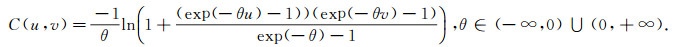
|
Frank Copula是对称的, 难以捕捉到上尾和下尾的相关变化.故若随机变量的相关结构可以由Frank Copula函数描述, 则说明该随机变量是对称的.
从以上三种Copula函数可以看出, 不同类型的Copula函数对数据的刻画是不同的, Gumbel Copula具有非对称的上尾相关性, Clayton Copula有非对称的下尾相关性.可见, 若用单一的Copula来对CPI与PPI相关性进行刻画, 得到的结果可能会不全面.而以往研究中均仅用单一的Copula函数来对CPI和PPI进行分析.故为使结果更具有说服力, 利用不同函数具有不同尾部相关性的特点, 提出混合Copula函数模型,即
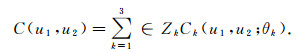
|
(1) |
其中C1, C2, C3分别为Clayton Copula, Gumbel Copula和Frank Copula; Z1, Z2, Z3分别为对应的权重参数, Z1+Z2+Z3=1, Z1, Z2, Z3∈[0, 1];θ1, θ2, θ3为模型的相依参数, 它反映了模型的相依结构.用此法既可以得到对称的统计模型, 又可以得到非对称的统计模型.尤其是对于尖峰, 厚尾的统计模型, 用该法可以十分有效得捕捉到其上下尾相关性结构, 进行更为有效的分析.
3 Copula函数的参数估计方法 3.1 边缘分布的核密度估计由于事先无法对各参数类型进行假设, 故采用非参数核密度估计[16]建立变量的边缘分布函数.
对于变量x, 当设n→∞, hn→∞(hn与n相关且hn>0)时,存在对x的概率密度函数f(x)的核估计
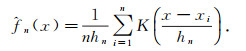
|
(2) |
其中, K(·)为核函数, hn为Parzen窗宽, 实际应用中常用经验法则来判断大小.由式(2)可得不同参数x, y边缘分布的非参数核密度估计
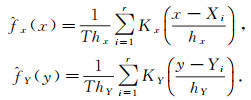
|
其中Kx, KY为核函数, hx, hY为窗宽.本文均采用正态核.
接着, 利用边缘密度函数得到边缘分布函数
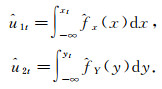
|
因为此处所用的核函数为正态核, 故可以得到
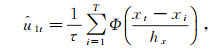
|
(3) |

|
(4) |
其中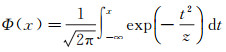
在利用核密度估计求得边缘密度函数之后, 将对其权重参数与相依参数进行估计.一般的参数估计方法有最大似然估计法, 分布最大似然估计法和半参数估计法.但这些方法仅适用于单一的变量较少的Copula函数.对于此处的混合Copula函数, 采用PL-EM-BFGS算法[17]来对其权重参数和相依参数进行估计.设(X, Y)的联合分布为

|
其中Θ=(αT, βT, ZT, θT)T,Z=(z1, z2, z3)T, Θ=(θ1, θ2, θ3)T.则其联合密度函数为
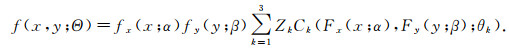
|
(5) |
其中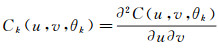
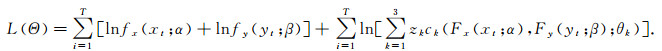
|
(6) |
其中(xt, yt), t=1, 2, …, T来自样本(X, Y), T为样本容量.
为防止模型失真, 引入惩罚函数[18].采用SCAD惩罚函数构建惩罚似然函数
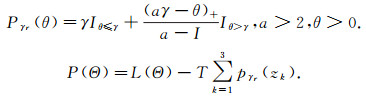
|
(7) |
其中γr为光滑参数.
对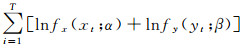
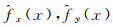
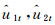
把边缘分布函数的估计值代入式(7)得
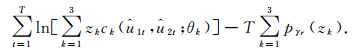
|
(8) |
对式(8)进行EM算法[19]估计.
EM算法主要有两步:第一步(E步)求期望; 第二步(M步)求极大值.设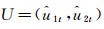
假设观测样本为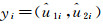
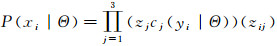

|
(9) |
第一步:
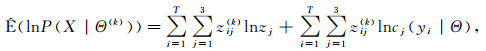
|
(10) |
其中K为迭代次数.此处是对L(Θ)求的E步, 而惩罚似然函数只是比L(Θ)多了一项-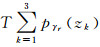

|
(11) |
第二步:利用拟牛顿法中的BFGS算法, 得到上述期望函数的最大值为

|
(12) |
由此即利用PL-EM-BFGS算法来得到Θ的参数估计值.
4 实证分析 4.1 数据选取选取1994年1月1日到2016年12月1日, CPI与PPI的月度价格指数的对数LNCPI和LNPPI作为样本数据, 共有275个居民消费者价格指数月度数据和275个生产者价格指数月度数据(数据来源为证券之星).涵盖时间长, 具有代表性.
由于CPI与PPI的月度价格指数主要受其环比增长率影响, 故计算两大指数的环比增长率来进行分析.记在第t个月CPI价格指数为P1t, PPI价格指数为P2t, 则其对应的环比增长率为

|
(13) |
为了使数据表现得更加明显, 在这里使用的环比增长率计算公式为

|
(14) |
分别对LNCPI与LNPPI的环比增长率进行描述性统计分析, 结果如表 1所示.
| 指标 | 均值 | 极大值 | 极小值 | 标准差 | 峰度 | 偏度 |
| LNCPI | -0.013 0 | 0.420 4 | -0.561 5 | 0.138 6 | 0.992 | -0.210 |
| LNPPI | -0.010 5 | 0.847 6 | -0.944 7 | 0.196 8 | 4.241 | -0.108 |
由表 1可以看到, LNCPI的平均环比增长率略大于LNPPI, 而其标准差略小于LNPPI.这说明LNPPI的波动性要略大于LNCPI的波动性.其偏度均小于零, 说明两者的密度函数重尾均在左侧, 而其峰度均大于零, 说明其属于尖峰分布.综上可知LNCPI与LNPPI的环比增长率均服从尖峰厚尾的分布, 适合用Copula拟合.
4.2 边缘分布的拟合选定高斯核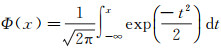

|
| 图 1 LNCPI与LNPPI环比增长率的核密度分布图 Fig.1 The kernel density distribution plot of LNCPI and LNPPI |
用PL-EM-BFGS方法对混合Copula函数进行拟合, 工具为Matlab 2013, 步骤如下:
(1) 取权重参数初值为Z=(1/3, 1/3, 1/3).
(2) 利用copulafit函数对单个Copula函数进行极大似然估计.所得极大似然估计的值作为其相依参数的初值, Θ=(0.247, 1.149, 1.503 3).
(3) 利用EM算法, 循环迭代50次, 得到权重和相依参数.
(4) 再利用copulafit函数对单一的copula函数进行参数估计.
(5) 最终各Copula函数的参数估计值结果如表 2所示.
| 函数名称 | 相依参数 | 权重参数 |
| Clayton Copula | θ_Clayton=0.247 9 | — |
| Gumbel Copula | θ_Gumbel=1.158 5 | — |
| Frank Copula | θ_Frank=1.503 3 | — |
| θ1=1.646 8×10-10 | Z1=0.281 6 | |
| Mix Copula | θ2=1.071 1 | Z2=0.365 6 |
| θ3=4.219 1 | Z3=0.352 8 |
常用的模型检验方法有赤池信息量准则(AIC)和最小欧式距离法[20].下文采用最小欧式距离法来判断模型拟合程度, 以体现混合Copula函数的优越性.首先引入经验Copula的定义.
定义2 如果(Xi, Yi), i=1, 2, 3, …, n, 为来自总体(X, Y)的简单随机样本, 则称
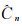
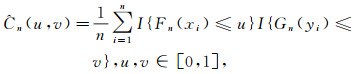
|
其中I(*)为示性函数, Fn(x), Gn(y)分别为随机变量X, Y的经验分布函数.
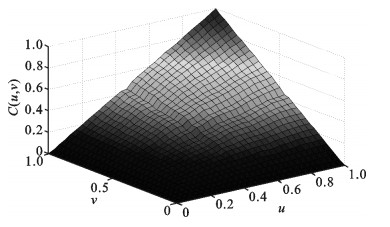
利用Matlab 2013绘图工具, 得到其经验分布函数如图 2所示.
|
| 图 2 LNCPI与LNPPI经验分布Copula Fig.2 The empirical distribution Copula of LNCPI and LNPPI |
利用各混合Copula的估计与经验Copula的估计的欧式距离作为模型优劣的衡量标准, 其欧式距离公式为
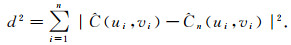
|
利用Matlab 2013, 得到混合Copula函数和其单一Copula函数的距离如表 3所示.从表 3中可以看出, 相比单一Copula函数, 混合Copula模型的欧式距离最小, 表明该模型能更好地拟合LNCPI与LNPPI环比增长率的原始特征, 是最优模型.
| 函数 | Clayton Copula | Gumbel Copula | Frank Copula | Mix Copula |
| 欧式距离 | 0.124 8 | 0.201 3 | 0.145 8 | 0.061 9 |
文中所提出的混合Copula模型, 能够综合单一Copula的优势, 并且利用权重参数来调节各个Copula函数的贡献大小, 从而使拟合效果更佳.同时通过描述性统计分析, LNCPI与LNPPI的环比增长率均存在尖峰厚尾的现象, 于是提出用非参数核密度估计的方法来建立变量的边缘分布函数.并且利用PL-EM-BFGS方法来对混合Copula的权重参数和相依参数进行估计.参数估计结果显示Z2比重最大, 说明混合Copula模型的相依结构更偏重于Gumbel Copula, 其数据更多地表现出下尾相关性.由此可以得到, CPI与PPI在经济下滑的过程中, 相关性表现得更为密切.故在经济不景气时期, 可以通过生产者价格指数对消费者价格指数进行预测分析, 及时给出合理的消费政策, 来阻止经济的进一步下滑.同样, 也可以用消费者价格指数对生产者价格指数进行预测, 及时扩大或缩小生产规模来应对经济衰退.此外, Frank Copula函数在混合模型中的参数相当大, 说明CPI与PPI在对称相关方面的相关性非常强, 即CPI与PPI之间同时上升与同时下降的比率相当高.最后利用欧式距离对模型与经验分布Copula函数进行计算检测, 得出混合Copula模型具有极好的拟合效果,适合LNCPI环比增长率与LNPPI环比增长率数据的相依结构, 未来可以利用此模型对CPI与PPI进行相关性分析, 并且及时利用两者之间的关系对经济现象做出措施, 来促进经济平稳运行.
| [1] |
何光辉. 中国CPI与PPI的结构与动态作用机制研究[J].
经济科学, 2009, 31(4): 15-30 HE Guanghui. Study on the structure and dynamic mechanism of CPI and PPI in China[J]. Economic Science, 2009, 31(4): 15-30 |
| [2] |
贺力平, 樊纲, 胡嘉妮. 消费者价格指数与生产者价格指数:谁带动谁?[J].
经济研究, 2008, 41(11): 16-26 HE Liping, FAN Gang, HU Jiani. CPI vs.PPI:Which drives which?[J]. Economic Research Journal, 2008, 41(11): 16-26 DOI:10.3969/j.issn.1674-8638.2008.11.004 |
| [3] |
徐伟康. 对《消费者价格指数与生产者价格指数:谁带动谁?》一文的质疑[J].
经济研究, 2010, 43(5): 139-147;158 XU Weikang. A query to the paper "CPI vs.PPI:Which drives which"[J]. Economic Research Journal, 2010, 43(5): 139-147;158 |
| [4] |
宋金奇, 舒晓惠. PPI与CPI的关系——基于误差修正模型的研究[J].
价格理论与实践, 2008, 28(10): 50-51 SONG Jinqi, SHU Xiaohui. The relationship between CPI and PPI——Based on the research of error correction model[J]. Price:Theory & Practice, 2008, 28(10): 50-51 |
| [5] | SKLAR A. Functions de repartition n dimensions et leurs marges[J]. Publication Institut Statistique Universite Paris, 1959, 8(1): 229-231 |
| [6] | NELSEN R B. An introduction to copulas[M]. New York: Springer, 1998. |
| [7] |
李悦, 程希骏. 上证指数和恒生指数的copula尾部相关性分析[J].
系统工程, 2006, 24(5): 88-92 LI Yue, CHENG Xijun. Tail dependence analysis of SZI & HIS based on Copula method[J]. Systems Engineering, 2006, 24(5): 88-92 |
| [8] |
李占雷, 李学师, 吴斯. 金融危机背景下沪综指与深成指指数相关性分析[J].
科技信息, 2010, 17(27): 116-117 LI Zhanlei, LI Xueshi, WU Si. The correlation analysis between Shanghai composite index and Shenzhen component index under the financial crsis[J]. Science & Technology Information, 2010, 17(27): 116-117 DOI:10.3969/j.issn.1673-1328.2010.27.112 |
| [9] |
孙志宾, 顾岚. Copula理论在金融中的应用[J].
广西师范大学学报(自然科学版), 2004, 22(2): 47-52 SUN Zhibin, Gu Lan. Copula theory and its application in finance[J]. Journal of Guangxi Normal University(Natural Science Edition), 2004, 22(2): 47-52 |
| [10] |
史道济, 姚庆祝. 改进Copula对数据拟合的方法[J].
系统工程理论与实践, 2004, 24(4): 49-55 SHI Daoji, YAO Qingzhu. A method of improving Copula fited to data[J]. Systems Engineering-Theory & Practice, 2004, 24(4): 49-55 |
| [11] | HU L. Dependence patterns across financial markets:A mixed Copula approach[J]. Applied Financial Economics, 2006, 16(10): 717-729 DOI:10.1080/09603100500426515 |
| [12] |
石建平, 景文宏, 李育峰. 连接函数Copula在我国物价指标相关性分析上的应用[J].
统计与决策, 2010, 16(20): 61-64 SHI Jianping, JING Wenhong, LI Yufeng. Application of Copula in correlation analysis of price index in China[J]. Statistics & Decision, 2010, 16(20): 61-64 |
| [13] |
佘雪峰. 消费者价格指数和生产者价格指数相关性研究——基于Copula函数[J].
技术经济与管理研究, 2014, 35(4): 11-20 SHE Xuefeng. Study on dependence between CPI and PPI——Based on Copula function[J]. Technoeconomics & Management Research, 2014, 35(4): 11-20 |
| [14] |
吕会琴, 赵文艺, 赵蕊. 厚尾相依序列均值多变点ANOVA型检验[J].
纺织高校基础科学学报, 2016, 29(1): 55-58 LYU Huiqin, ZHAO Wenyi, ZHAO Rui. An Anova-type test for multiple change points in the mean of heavy-tailed dependent sequence[J]. Basic Sciences Journal of Textile Universities, 2016, 29(1): 55-58 |
| [15] | WU Shaomin. Construction of asymmetric copulas and its application in two-dimensional reliability modelling[J]. European Journal of Operational Research, 2014, 238(2): 476-485 DOI:10.1016/j.ejor.2014.03.016 |
| [16] | HU Shunbo, JIANG Zhaolin, ZHU Xiangrong. Research on Parzen window based on improved Gaussian matrix in medical image registration[J]. Journal of Computational Information Systems, 2012, 8(12): 5013-5110 |
| [17] |
黄雁勇. 混合Copula模型的选择、估计及其应用[D]. 西安: 西安交通大学, 2010: 17-24.
HUANG Yanyong.Selection estimation of hybrid Copula model and its application[D].Xi'an:Xi'an Jiaotong University, 2010:17-24. |
| [18] |
赖学方, 贺兴时. 一种带有自适应惩罚权重的惩罚最小一乘估计[J].
纺织高校基础科学学报, 2016, 29(4): 471-477 LAI Xuefang, HE Xingshi. A method of least absolute deviation estimator with adaptive weighted penalty[J]. Basic Sciences Journal of Textile Universities, 2016, 29(4): 471-477 |
| [19] | KOLEE, KOEDIJK K, VERBEEK M. Selecting Copulas for:Risk management[J]. Journal of Banking and Finance, 2007, 31(8): 2405-2423 DOI:10.1016/j.jbankfin.2006.09.010 |
| [20] |
赵美玲. Copula理论以及在金融风险管理中的应用[D]. 扬州: 扬州大学, 2015: 22-23.
ZHAO Meiling.The theory of Copula and its application in financial risk management[D].Yangzhou:Yangzhou University, 2015:22-23. |



