0 引言及预备

拓扑空间中紧性、连通性与分离性一直是研究者们关注的问题之一.潘伟等^[1-3]研究了LF拓扑空间中的可数L-模糊半紧性、γ-良紧性和α-p连通性.在此基础上, 文献[4-6]利用半开U_a-覆盖引入半N_U-紧性，定义强N_β-紧性并研究模糊紧半闭集的性质，定义LF拓扑空间中良拟紧性并证明了在LF半正则空间等价于良紧性.文献[7-9]将其推广, 利用α-远域族定义LF拓扑空间中F紧性和可数强F紧性, 推广Wallman紧化并提出拓扑空间的n-点紧化.李南南^[10]定义α-开运算, 借助α-开运算定义α-紧并研究其性质.文献[11-13]将LF拓扑空间中理论推广至LF双拓扑空间中, 研究了LF双拓扑空间中可数配超紧性、配超紧性和几乎可数层仿紧性.文献[14-15]利用非标准分析方法对拓扑空间中的紧性、相对紧性及局部紧性等分别进行非标准刻画, 对研究紧性提供了新的研究视角.尤飞等^[16-17]借助美国数学家Mashhxur^[18]提出的分明闭包空间的概念, 将LF拓扑空间中好的性质推广至LF闭包空间, 进一步丰富了LF闭包空间中紧性的研究.

在前人研究的基础上, 沿弱化方向从层次结构入手, 定义了LF闭包空间的一种新的仿紧性—几乎可数仿紧性, 刻画其基本特征并证明其具有一些较好的拓扑性质.文中用L表示F格, L的最大元是1, 最小元是0且1≠0.M(L)与M^*(L^X)分别表示L与L^X的非零分子之集, P(L)表示L的非1素元之集.L^X表示X上的全体LF集, 其最大元与最小元分别是1_X和0_X.∨A和∧A分别指集A的上确界和下确界, β^*(α)指α的最大极小集.

其他未说明的概念与符号均见文献[19].

定义1^[18]  设L是完全分配格, 若映射~:L^X→L^X满足(1)0^~=0;(2)A≤A^~(∀A∈L^X); (3) (A∨B)^~=A^~∨B^~(∀A, B∈L^X), 则称~是L^X上的一个闭包算子, 且称(L^X, ~)为一个LF闭包空间.

定义2  设(L^X, ~)为一个LF闭包空间, 其中~:L^X→L^X, Λ={(P^~)^x:P∈L^X}.

(1) x_α∈M(L^X), (P^~)^x∈Λ, 若x_α≮(P^~)^x, 则称(P^~)^x为x_α的几乎包域.分子x_α的一切几乎包域之集, 记作C^x(x_α).

(2) A∈L^X, ϕ⊂Λ, 若∀x_α∈A, ∃(P^~)^x∈ϕ使得(P^~)^x∈C^x(x_α).则称ϕ为A的几乎α-包域族, 记作∧ϕ≺A(α).若∃r∈β^*(α)使∧ϕ≺A(r), 则称ϕ为A的几乎α^--包域族, 记作∧ϕ≺≺A(α), 其中α∈M(L).

定义3^[20]  设(L^X, ~)为一个LF闭包空间, A∈L^X, α∈M(L).Ω={A_t:t∈T}是一族LF集.如果对于∀x_α≤A, 存在分明集P使得P^~∈C(x_α)以及T的有限子集T₀, 使∀t∈T-T₀, A_t≤P^~, 则称Ω在A中α-局部有限.当A=1_X时, 简称Ω是α-局部有限族.

定理1  设f:(L^X₁, ~₁)→(L^X₂, ~₂)是连续的L-Zadeh型函数, A∈L^X₂, α∈M(L).若Δ⊂L^X₂在A中α-局部有限, 则f^-1(Δ)={f^-1(B)|B∈Δ}在f^-1(A)中α-局部有限.

证明  设x_α≤f^-1(A), 则f(x)_α=f(x_α)≤A.由Δ在A中α-局部有限知, 存在分明集Q使Q^~∈C(f(x_α))以及{B₁, B₂, …, B_n}⊂Δ使得∀B∈Δ-{B₁, B₂, …, B_n}, B≤Q^~.

设P=f^-1(Q), 则P为分明集且P^~=f^-1(Q^~), 则由f的连续性知P^~∈C(x_α).这时∀f^-1(B)∈f^-1(Δ)-{f^-1(B₁), f^-1(B₂), …, f^-1(B_n)}, f^-1(B)≤P^~, 故f^-1(Δ)在f^-1(A)中α-局部有限.

1 几乎可数仿紧性的定义

定义4  设(L^X, ~)是LF闭包空间, A∈L^X, α∈M(L), 称A是几乎可数α-仿紧的, 若对A的任一可数几乎α^--包域族Ω, 存在Ω的有限子族Ψ, 使得

(ⅰ)Ψ是A的几乎α^--包域族;

(ⅱ)Ψ是Ω的余加细;

(ⅲ)Ψ′∧A={D′∧A|D∈Ψ}在A中α-局部有限.

若对∀α∈M(L), A都是几乎可数α-仿紧的, 则称A几乎可数仿紧的.如果A=1_X是几乎可数α-仿紧的(几乎可数仿紧的), 则称空间(L^X, ~)是几乎可数α-仿紧的(几乎可数仿紧的).

定理2  在LF闭包空间中, 可数仿紧性⇒几乎可数仿紧性.

引理1  设(L^X, ~)是LF闭包空间, A∈L^X, (B^~)^x, (C^~)^x∈Λ且α∈M(L), 则

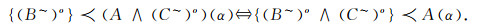
证明  必要性:设x^α≤A∧(C^~)^x, 则由{(B^~)^x}≺(A∧(C^~)^x)(α)知, x^α≤/(B^~)^x, 当然x^α≤/(B^~)^x∧(C^~)^x, 故{(B^~)^x∧(C^~)^x}≺A(α).

充分性:由{(B^~)^x∧(C^~)^x}≺A(α)知, x^α≤/(B^~)^x∧(C^~)^x, 又因为x^α≤/(C^~)^x, 故x^α≤/(B^~)^x.i.e., {(B^~)^x}≺(A∧(C^~)^x)(α).

定理3  设(L^X, ~)是LF闭包空间, A∈L^X, 则A是几乎可数仿紧集的充要条件是A∧(B^~)^x是几乎可数仿紧集((B^~)^x∈Λ).

证明  必要性:设(C^~)^x∈Λ, x_α≤A∧(B^~)^x且{(C^~)^x}≺(A∧(B^~)^x)(α).由引理1可知, {(B^~)^x∧(C^~)^x}≺A(α).又因为A是几乎可数仿紧集, 所以∃r∈β^*(α)使得{(B^~)^x∧(C^~)^x}≺A(r).再由引理1知{(C^~)^x}≺(A∧(B^~)^x)(r), 即{(C^~)^x}≺≺(A∧(B^~)^x)(α), 故A∧(B^~)^x几乎可数仿紧的.

充分性:设∀(B^~)^x∈Λ, A∧(B^~)^x是几乎可数仿紧集, x_α≤A∧(B^~)^x, (C^~)^x∈Λ且{(C^~)^x}≺(A∧(B^~)^x)(α).

由引理1知{(B^~)^x∧(C^~)^x}≺A(r).下面只需证{(B^~)^x∧(C^~)^x}≺≺A(α).

事实上, 由A∧(B^~)^x是几乎可数仿紧集及{(C^~)^x}≺(A∧(B^~)^x)(α)知, ∃r∈β^*(α), {(C^~)^x}≺(A∧(B^~)^x)(r), 再由引理1知{(B^~)^x∧(C^~)^x}≺A(r).即{(B^~)^x∧(C^~)^x}≺≺A(α), 所以A是几乎可数仿紧的.

推论1  LF闭包空间中的几乎可数仿紧性对于闭包算子~的像集是可遗传的.

2 几乎可数仿紧性的性质

定义5^[16]  设L₁和L₂是完全分配格, f:X→Y和F:L^X₁→L₂^Y均是映射, 若F满足(1)F(0)=0;(2)F和F^-1均是保并映射, 则称F为广义序同态.这里

特别地, 当L₁=L₂=L时, 称上述定义的广义序同态F为由f诱导出的L值Zadeh型函数.

定义6^[16]  设(L^X, ~)和(L^Y, ~)均为LF闭包空间(为方便起见, L^X, L^Y上的两个闭包算子用同一记号~表示), f:(L^X, ~)→(L^Y, ~)为广义序同态, 若∀A∈L^X, f(A^~)≤[f(A)]^~, 则称f是连续的.

定义7^[16]  设(L^X, ~)和(L^Y, ~)均为LF闭包空间, 若存在一一的满的L值Zadeh型函数f:(L^X, ~)→(L^Y, ~)且f和f^-1都连续, 则称(L^X, ~)与(L^Y, ~)强同胚, f称为强同胚映射, 被强同胚映射所保持的性质称为弱同胚不变性质.

定理4  设(L^X, ~)和(L^Y, ~)均为LF闭包空间, f:(L^X, ~)→(L^Y, ~)是由F诱导出的连续的L值Zadeh型函数, 则当A是(L^X, ~)中的几乎可数仿紧集时, f(A)是(L^Y, ~)中的几乎可数仿紧集.

证明  设Ω是f(A)的几乎可数α^--包域族(α∈M(L)), 则不难验证f^-1(Ω)={f^-1((P^~)^x):(P^~)^x∈Ω}是A的几乎可数α^--包域族.于是存在A的几乎α^--包域族Ψ, 使Ψ是f^-1(Ω)的余加细, 且Ψ′∧A在A中α-局部有限.考虑f(Ψ)={f((P)^x):(P)^x∈Ψ}, 则f(Ψ)是f(A)的几乎α^--包域族且f(Ψ)是Ω的余加细.

∀y_α∈f(A), 存在惟一的x∈X, 使f(x)=y, x_α∈A, 从而存在分明闭集R使(R^~)^x∈C^x(x_α)且存在有限子集Ψ₀⊂Ψ, 使∀P^x∈Ψ-Ψ₀, (P′)^x∧A≤R^~.显然f(R)是分明闭集, 且f(R)^~∈C^x(x_α).由于f是连续映射, 故∀P^x∈Ψ-Ψ₀, f(P^x)=f(Ψ)-f(Ψ₀), 且(f(P^x))′∧f(A)=f((P^x)′)∧f(A)=f((P^x)′∧A)≤f(R^~)=(f(R))^~.所以(f(Ψ))′∧f(A)在f(A)中α-局部有限.

推论2  LF闭包空间中的几乎可数仿紧性是弱同胚不变性质.

定理5  设(L^X, ~)和(L^Y, ~)均为LF闭包空间, f:(L^X, ~)→(L^Y, ~)是由F诱导出的连续的L值Zadeh型函数, 则当B是(L^Y, ~)中的几乎可数仿紧集时, f^-1(B)是(L^X, ~)中的几乎可数仿紧集.

证明  设Ω是f^-1(B)的几乎可数α^--包域族(α∈M(L)), 则不难验证f(Ω)={f((P^~)^x):(P^~)^x∈Ω}是B的几乎可数α^--包域族.于是存在B的几乎α^--包域族Ψ, 使Ψ是f(Ω)的余加细, 且f(Ω)′∧B在B中α-局部有限.考虑f^-1(Ψ)={f^-1((P^~)^x):(P^~)^x∈Ψ}, 则f^-1(Ψ)是f^-1(B)的几乎α^--包域族且f^-1(Ψ)是Ω的余加细.

∀x_α∈f^-1(B), 存在惟一的y∈Y, 使f^-1(y)=x, y_α∈B, 从而存在分明闭集R使得(R^~)^x∈C^x(x_α)且存在有限子集Ψ₀⊂Ψ, 使∀P^x∈Ψ-Ψ₀, (P^x)′∧B≤R^~.显然f^-1(R)是分明闭集, 且f^-1(R)^~∈C^x(x_α).由于f是连续映射, 故∀P^x∈Ψ-Ψ₀, f^-1(P^x)=f^-1(Ψ)-f^-1(Ψ₀), 且

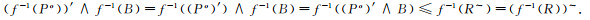
所以(f^-1(Ψ))′∧f^-1(B)在f^-1(B)中α-局部有限.

定义8  设X≠∅, (X, ~)是分明闭包空间, 若(X, ~)的每个可数余覆盖都有局部有限的几乎子余覆盖, 则称(X, ~)为几乎可数仿紧空间.

引理2^[19]  设L是完全分配格, 则L中每个元均可表示为比它小的分子之并.

定义9^[21]  设(L^X, ω_L(~))是由分明闭包空间(X, ~)诱导出的LF闭包空间, 若P是(L^X, ω_L(~))的某种性质, 当且仅当(X, ~)也具有性质P, 那么称性质P是“L-好的推广”.

定理6  设(L^X, ω_L(~))是由分明闭包空间(X, ~)诱导出的LF闭包空间, 则(L^X, ω_L(~))是几乎可数仿紧空间当且仅当(X, ~)是几乎可数仿紧空间.

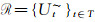
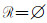
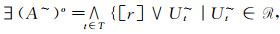
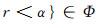
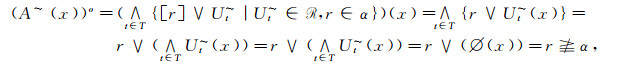
证明  必要性:设(L^X, ω_L(~))是几乎可数仿紧空间, 是(X, ~)的可数余覆盖, 即∧, 由引理2知L的最大元1可表示为若干分子之并, 任取这样一个分子α, 令Φ={(P^~)^x∈ω_L(~)}, 其中(P^~)^x=∧{[r]∨U^~|P^x≤[r]∨U^~, U⊂X, r < α}, 则, 可知,

当且仅当(A^~)^x∈C(x_α), 所以Φ是1_X的几乎α^--包域族.因为(L^X, ω_L(~))是几乎可数仿紧空间, 所以有局部有限子族使Φ有局部有限子族Ψ={(A₁^~)^x, (A₂^~)^x, …，(A_n^~)^x}是1_X的几乎α^--包域族.

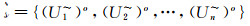
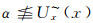
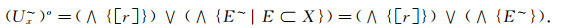
充分性:设(X, ~)是几乎可数仿紧空间.Φ是(L^X, ω_L(~))的几乎α^--包域族, α∈M(L), 这时, ∀x∈X, 可取(U_x^~)^x∈Φ, (U_x^~)^x=∧{[r]∨E^~|U_x≤[r]∨E^~, E⊂X, r < α}使得, 由引理2知

令, 则.由知, .由r < α知, 是恒成立的，又由α>0知, , 也即是(X, ~)的几乎可数余覆盖.

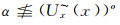
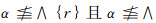
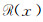
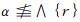
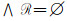
上述证明说明Φ中的成员是满足r＜α且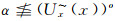的(U_x^~)^o∈Φ的全体.因为(X，~)是几乎可数仿紧空间，所以有局部有限子族构成(X，~)的几乎可数余覆盖，即，令Ψ＝{(U^~_x1)^o，(U^~_x2)^o，…, (U^~_xn)^o}，其中(U^~_xi)^o＝∧{[r]∨(E_i^~)^o}|(U_xi)^o≤[r]∨(E_i^~)^o，(E_i)^o⊂X，r＜α，α∈M(L)}.

下证Ψ是几乎α^--包域族.∀x∈X，总

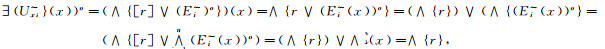
所以总∃s∈{r|r＜α}⊂β^*(α)使得.即Ψ是几乎α-包域族.所以(L^X，ω_L(~))是几乎可数仿紧空间.

推论3  LF闭包空间的几乎可数仿紧性是“L-好的推广”.