2. Department of Mathematics, Anand International College of Engineering, Jaipur 303012, Rajasthan, India;
3. Department of Mathematics, Weinan Normal University, Weinan 714000, Shaanxi, China
2. 阿南德工程国际学院 数学学院, 印度 拉贾斯坦邦 斋浦尔 303012;
3. 渭南师范学院 数学学院, 陕西 渭南 714000
This note is a companion to the forth-coming paper[1]. For the details on the Kuznetsov trace formula, cf. the extended survey [2-6], etc.
The main objective is to prove Theorem 1.3 whence the reverse Kuznetsov trace formula, Theorem 2.4. The raison-d′être for this note is the following. There is no direct proof of Theorem 2.4 in [3], it is derived by reversing the Kuznetsov trace formula, which in turn is proved via Fay′s functional equation which comes from the theory of resolvent and is not easily accessible. In[5], the proof is given in the lines of Selberg-Kuznetsov but the outlook of the statement is different since the Neumann series is replaced by something else. This gap has been filled in the companion paper[1] in a sketchy way with the aid of Meijer G-functions. We hereby provide new proofs of some formulas involving Bessel functions which are only sketched in [1], and in [3] and [5], proofs are not given or given in an inexplicit way.
As in these papers, we mainly follow the notation of Iwaniec[3]. The notation for special functions are from [7]. For comparison′s sake, we state the trace formulas in the form of a Fuchsian group of the first kind and so the cusps are to be understood to mean ∞ when one thinks of the full modular group.
Let S(m, n; c) be the classical Kloosterman sum defined as
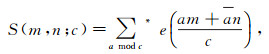
|
(1) |
where the summation is over relatively prime residues a mod c with a denoting the multiplicative inverse of a.
In [3] the Whittaker function is defined by
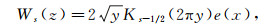
|
(2) |
which satisfies the symmetry condition.
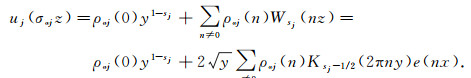
|
(3) |
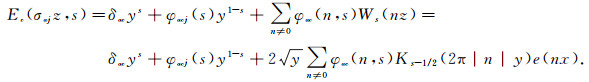
|
(4) |
Here λaj(n) and φac(n, 1/2+it) are the Fourier coefficients of (a complete orthonormal system of) Maass forms ([8]) and the eigen packet of Eisenstein series in 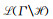
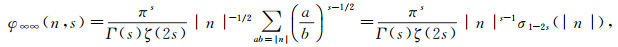
|
(5) |
where σ indicates the sum-of-divisors function[3].
On [3], the normalization is introduced, which we will use in this paper:
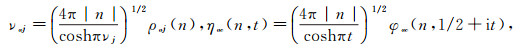
|
(6) |
for n≠0.
We call any C2-function f(x) on [0, ∞] a test function if it satisfies the condition
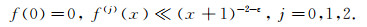
|
(7) |
The following theorem is stated as the Bruggeman-Kuznetsov formula on [3] (known as the Kuznetsov trace formula, cf.[9-11].
Theorem 1 (Kuznetsov [12]) Let 
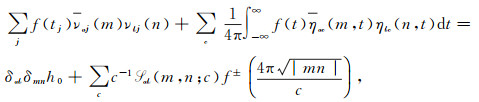
|
(8) |
where f± are given on [3].
The Kuznetsov trace formula is a sort of the Poisson summation formula ([3]) which is equivalent to the functional equation (cf.[13]) and so Theorem 1 may be proved most naturally as a consequence of the functional equation in Theorem 2 (due to Fay [14]) for the Kloosterman sums zeta-function with Bessel function weight Zs(m, n)[3].
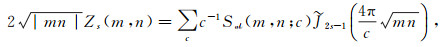
|
(9) |
where
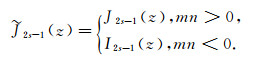
|
(10) |
Theorem 2 (Fay[14]) The series Zs(m, n) has an analytic continuation over the whole s-plane and satisfies the functional equation
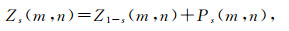
|
(11) |
where Ps(m, n) is the residual function given by
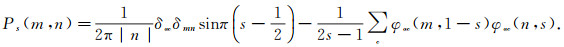
|
(12) |
Proof of Theorem 1 from Theorem 2 is given on [3].
On the other hand, the Kloosterman sums zeta-function Ln(m, n) is defined by
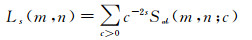
|
(13) |
and studied by Selberg[15] and later by Goldfeld and Sarnak[16].In [1] the following was proved as an important corollary to Lemma 1.Our main purpose is to give a detailed proof of this theorem and thence of Theorem 7.
Theorem 3 For integers m, n > 0 and Re s > 1/4, we have
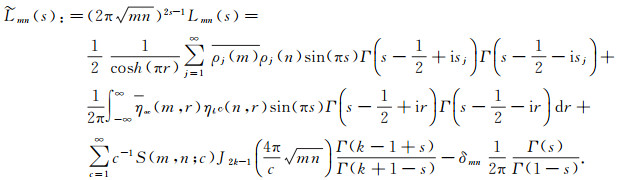
|
(14) |
As described on [3] and on [17], the reverse Kuznetsov trace formula is to be regarded as an expansion in J-Bessel functions due to Sears and Titchmarsh[18] and in many literature this reversed form is referred to as the Kuznetsov trace formula[17, 19-21]. In [1-2] we referred to it as the Kuznetsov sum formula, whence the title, since it gives an expression for the sum of Kloostermann sums with the test function in terms of eigen-values of the automorphic Laplacian. Since in the case mn < 0, the Kuznetsov trace formula is completely reversed as given on [3], we concentrate on the case m, n > 0.
Let f(x) be a continumous function of bounded variation on R+ such that
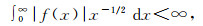
|
(15) |
in particular f(x) may be an infinitely many times differentiable function with compact support. We follow [3] which gives the clearest exposition thereof.
Let f0 be the projection of f on the space spanned by odd indexed Bessel functions {J2n+1|n≥0} and is given by the Neumann series

|
(16) |
and

|
(17) |
is the Neumann integral.In [21] Ven this formula is stated with a typo of 2ir which should be 2n+1.
On the other hand, let
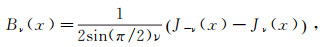
|
(18) |
and define the Titchmarsh integral Tf(t) by
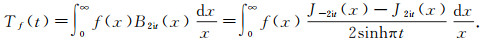
|
(19) |
Then define the continuous superposition of projections of f on B2it by
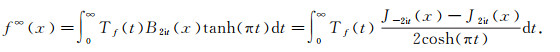
|
(20) |
Theorem 4 (Sears-Titchmarsh inversion) We have the Sears-Titchmarsh inversion
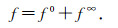
|
(21) |
Also define the constant
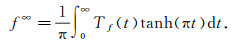
|
(22) |
Theorem 5[3] Let 
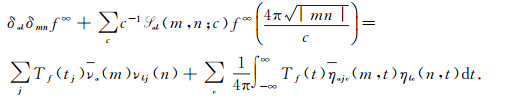
|
(23) |
It seems that the corresponding formulas in [17] are incorrect in comparison with other refs.
Let 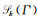
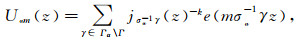
|
(24) |
where j is the denominator appearing in
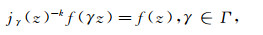
|
(25) |
so that
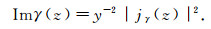
|
(26) |
Let fjk be orthogonal basis. Let

|
(27) |
be the expansion of Poincaréseries with respect to this basis.The exact complement to Theorem 5 is
Theorem 6[3] Let 
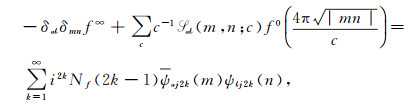
|
(28) |
where ψajk(m) are the normalized Fourier coefficients

|
(29) |
Adding Theorems 5 and 6 in view of the Sears-Titchmarsh inversion give the reversed Kuznetsov sum formula in contrast to Theorem 1.
Theorem 7[3] Let 
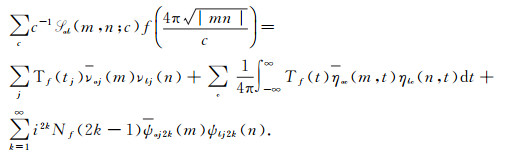
|
(30) |
Remark 1 We remark that Theorem 4 coincides with [5]. Since in the latter, the Neumann series part ([5, (2.2.6)] is replaced by [5, (2.2.9)], it has a seemingly different outlook.
Using the Hankel transform, Theorem 4 may be clearly understood as a procedure corresponding to the mapping x↔1/x under which the intervals (0, 1) and (1, ∞) map each other.
The Hankel transform of order 0 with Re v > -1/2 is defined by
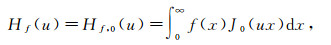
|
(31) |
for y > 0 which has admits the inversion formula
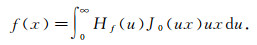
|
(32) |
Then the Neumann series (16) may be expressed as

|
(33) |
Proof is given [3] and depends on the formula
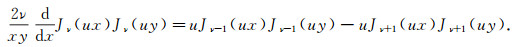
|
(34) |
Integrating over 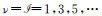
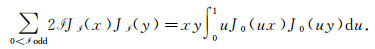
|
(35) |
Multiplying (36) by f(y)y-1 and integrating in y, we obtain
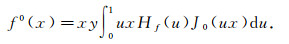
|
(36) |
By the Sears-Titchmarsh inversion (15) and the Hankel inversion (32), we conclude that
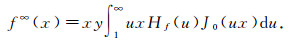
|
(37) |
Hence we conclude that the Sears-Titchmarsh inversion is a counter part of the division of the real line into two parts, which then is responsible for the functional equation. Thus the Sears-Titchmarsh is a counterpart of the functional equation and this explains the reverse Kuznetsov formula is also deduced from the zeta-symmetry as the Kuznetsov formula has been most naturally deduced from Fay′s functional equation in Theorem 2.
We note the following correspondence between groups. The right half-plane is represented by the positive real axis, which is a multiplicative group, in view of analytic continuation. And the Spiegelung τ↔-1/τ, which is one of the generators of the modular group, corresponds to the inversion x↔1/x under which the two intervals (0, 1) and (1, ∞) maps into each other.
In the Riemann zeta-case, the variables are connected by

|
(38) |
because of the presence of a simple pole at s = 1, the right-half plane is narrowed down to Re s > 1, the domain of absolute convergence, leaving the critical strip 0 < σ < 1 so mysterious (cf.22).
Proof of (36).We use two well-known formulas
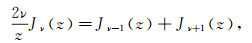
|
(39) |
and
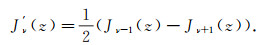
|
(40) |
Since
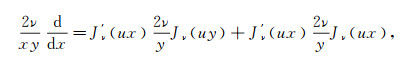
|
(36) follows on substituting above formulas.
3 Proof of Theorem 3We shall prove Theorem 3 whence Theorem 7 by modifying Motohashi′s argument[5] and under the assumption that
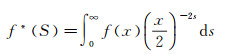
|
(41) |
or
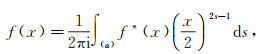
|
(42) |
and
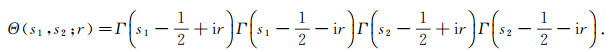
|
(43) |
We appeal to
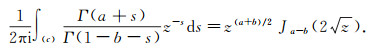
|
(44) |
This is applied to the essential case appearing on [5, (2.4.13)]:
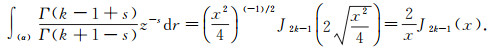
|
(45) |
Another formula to be used is
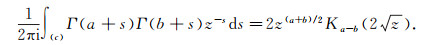
|
(46) |
This is applied in the special case
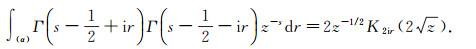
|
(47) |
For the proof of Theorem 7 we need two more well-known formulas
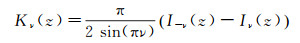
|
(48) |
and
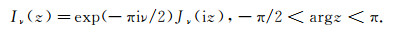
|
(49) |
In Motohashi [5], the integral
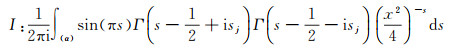
|
(50) |
is computed in an indirect way and the result reads

|
(51) |
Proof of (51).
A common procedure is to apply Euler′s formula and rewrite it as

|
(52) |
Putting 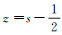
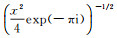
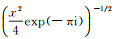
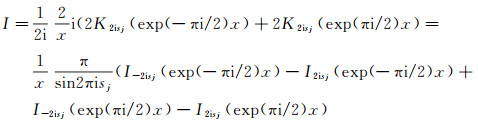
|
(53) |
by (48). Hence by (49)
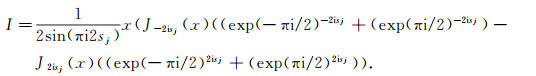
|
(54) |
Hence we arrive at (51), completing the proof.
The real analytic Poincaré series is defined on [23] which is referred to in[1], We use the one defined on [5]
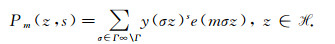
|
(55) |
The key idea for trace formulas is due to Selberg[15, 24] and depends on two ways of expressing the inner product of two Poincaré series
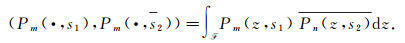
|
The inner product of Poincaré series is computed in Motohashi[5] for integers m, n > 0. Equating the Unfolding formula and the Parseval formula, we deduce the following theorem. For the proof cf.[1] and [2].
Lemma 1 (Unfolding=Parseval formula), [5 Lemma 2.2] Let { uj } be as in (3). Then for sj ′s satisfying Re s2+α > Re s1 > α+1/4 and Re sj > 3/4, j=1, 2 we have
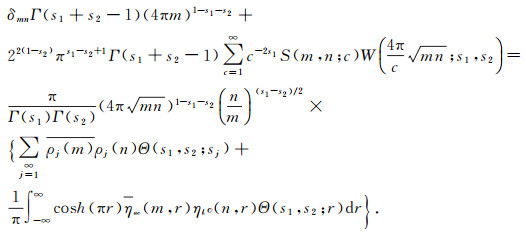
|
(56) |
where [5]
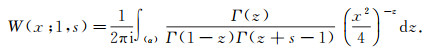
|
(57) |
Proof of Theorem 3.
In Lemma 1 we choose s1=1, s2=s with Re s > 1-α for 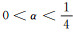
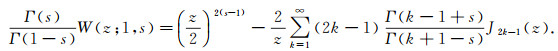
|
(58) |
(43) amounts to
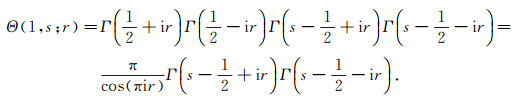
|
(59) |
(56) reduces to
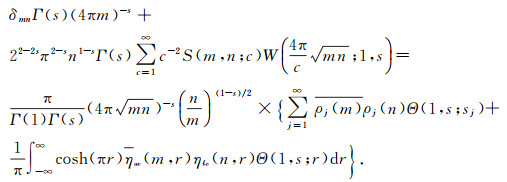
|
(60) |
Dividing both sides by Γ(1-s), we led to the form to which we may apply (58).

|
(61) |
Dividing both sides by 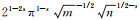
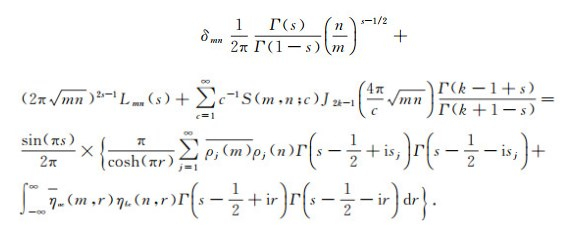
|
(62) |
Since
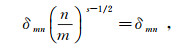
|
(62) leads to (14) completing the proof.
Proof of Theorem 7 We multiply (14) by f(x) in the form (42) interchange the order of integration and appeal to the known formulas for Bessel functions (46), (48), and (49) successively.
| [1] | MA J, AGARWAL P. On the Kuznetsov sum formula, to appear. |
| [2] | AGARWAL P, KANEMITSU S, MA J. On the Kuznetsov sum formula[C]//Proc ICSFA, 2016. |
| [3] | IWANIEC H. Introduction to the spectral theory of automorphic forms[J]. Matemática Iberoamericana, Revista Mateatica Iberoarmericana, 1995 |
| [4] | LIU J, YE Y. Petersson and Kuznetsov trace formulas[M]. . New York: Amer Math Soc and International Press, 2005: 147-168. |
| [5] | MOTOHASHI Y. Spectral theory of the Riemann zeta-function[M]. . Cambridge: Cambridge UP, 1997. |
| [6] | YE Yangbo. Automorphic forms and trace formulae[M]. . Beijing: Peking University Press, 2001. |
| [7] | MAGNUS W, OBERHETTINGER F, TRICOMI F G. Higher transcendental functions[M]. . New York: McGraw-Hill, 1953. |
| [8] | MAASS H. Vber eine neue art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen[J]. Math Ann, 1949, 121: 141-183 DOI:10.1007/BF01329622 |
| [9] | BRUGGEMAN R. Fourier coefficients of cusp forms[J]. Invent Math, 1978, 45: 1-18 DOI:10.1007/BF01406220 |
| [10] | BRUGGEMAN R. Fourier coefficients of automorphic forms[M]. . New York/Berlin: Springer Verl, 1981. |
| [11] | PROSKURIN N V. Sum formulas for Kloosterman sums[J]. Zap Naun Sem LOMI, 1979, 82: 103-135 |
| [12] | KUZNETSOV N V. Petersson's conjecture for cusp forms of weight zero and Linnik's conjecture[J]. Sums of Kloosterman sums, Mat Sb(N.S.), 1980, 111(153): 334-383 |
| [13] | KANEMITSU S, TSUKADA H. Contributions to the theory of zeta-functions——Modular relation supremacy[M]. . London: World Sci, 2014. |
| [14] | FAY J D. Fourier coefficients of the resolvent for a Fuchsian group[J]. J Reine Angew Math, 1997, 293/294: 143-203 |
| [15] | SELBERG A. On the estimation of Fourier coefficients of modular forms[J]. Proc Symp Pure Math AMS, 1965, 8: 1-15 DOI:10.1090/pspum/008 |
| [16] | GOLDFELD D, SARNAK P. Sums of Kloosterman sums[J]. Invent Math, 1983, 71: 243-250 DOI:10.1007/BF01389098 |
| [17] | BAKER R C. Kloosterman sums and maass forms[M]. . Heber City: Kendrick Press, 2003. |
| [18] | SEARS D B, TITCHMARSH E C. Some eigenfunction formulae[J]. Proc London Math Soc, 1954, 1(2): 165-175 |
| [19] | MIATELLO R, WALLACH N R. Kuznetsov formulas for real rank one groups[J]. J Funct Anal, 1990, 93: 171-206 DOI:10.1016/0022-1236(90)90138-B |
| [20] | GOODMAN R, WALLACH N R. Whittaker vectors and conical vectors[J]. J Funct Anal, 1980, 39: 199-279 DOI:10.1016/0022-1236(80)90013-0 |
| [21] | VENKOV A B. Spectral theory of automorphic function and its applications[M]. . Dordrecht/Boston, London: Kluwer Academic Publishers, 1990. |
| [22] | TITCHMARSH E C. The theory of the Riemann zeta-function[M]. 2nd ed. Oxford: Clarendon Press, 1986. |
| [23] | VENKOV A B. Spectral theory of automorphic functions[J]. Trudy Mat Inst Steklov, 1981, 153: 3-171 |
| [24] | SELBERG A. Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series[J]. J Indian Math Soc, 1956, 20: 47-87 |



