聚类分析是数据挖掘、统计学、生物学、市场营销、模式识别和信息检索等领域应用非常广泛的技术[1].K-均值是基于划分的聚类算法, 该算法简单且易于使用, 运行速度快, 与其他聚类算法相比应用更加广泛[2].但是, K-均值算法也存在着一定的局限性, 聚类结果受初始中心点的影响较大, 容易陷入局部极小值[3].针对上述局限性, 很多学者对K-均值算法进行了改进研究.文献[4-7]通过与具有全局寻优能力的进化算法或优化算法相结合, 改善了K-均值算法易陷入局部极值的问题, 文献[8]提出一种基于改进多目标萤火虫优化算法的模糊聚类方法, 有效解决了传统的模糊聚类算法无法获得全面、准确的聚类结果的问题; 文献[9]提出一种基于杜鹃搜索算法的K-均值聚类方法, 有效地改善K-均值算法易陷入局部极值的缺点; 文献[10]提出基于扰动因子的相似度下的聚类算法, 有效地克服了K-均值聚类算法存在的陷入局部最优,对异常数据敏感的缺点, 使得算法产生的聚类结果更趋于稳定.
文献[11-12]提出了一种在迭代过程中加入高斯扰动的方法, 有效地提高了算法的收敛速度.文献[13]采用随机选择的方式进行变异和扰动操作, 增加种群的多样性, 平衡算法的局部搜索能力和全局搜索能力, 加快了人工蜂群算法的收敛速度; 文献[14]将自适应混沌引入差分进化算法, 然后将所得算法融合到粒子群优化算法, 使得局部搜索能力增强, 进一步提高了算法的求解精度和效率; 文献[15]将混沌优化和遗传算法结合起来提高局部搜索性能.从以往的研究可以看出, 利用元启发式算法与智能算法结合, 是一个较为可行的解决方案, 但现有研究还存在问题, 由于元启发式算法也存在容易陷入极值的缺点, 如果直接利用元启发式算法和智能算法结合, 则最终的聚类结果也不一定理想.鉴于此, 本文首先利用基于蚁群觅食行为的聚类算法搜寻K-均值的初始聚类中心, 然后在此基础上建立基于扰动因子的准则函数下的聚类算法.该算法通过给准则函数增加一组随着迭代次数递减的扰动因子来保持搜索过程中解的多样性, 增大局部搜索范围, 以达到提高聚类效果的目的.
1 初始聚类中心搜寻 1.1 蚁群聚类算法蚁群聚类算法是由P. S. Shelokar提出的用于解决聚类问题的蚁群算法[16].蚁群算法是一种仿生进化算法, 具有很强的鲁棒性和全局优化能力[17].基于蚁群觅食行为的聚类算法是聚类数目已知的聚类算法, 需要取定聚类的数目k.
1.2 基于蚁群聚类算法的初始聚类中心的搜寻X={X|xi=(xi1, xi2, …, xim), i=1, 2, …, N}为样本数据集, 表示样本集所包含N个数据, 每个数据有m个属性.在初始化阶段, 首先要随机选择k个数据作为初始聚类中心, 并初始化信息素矩阵, 即τij(0)=0.利用式(1) 更新各路径上信息素浓度τij(t):
| ${\tau _{ij}}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}}\left( t \right),$ | (1) |
其中:ρ为信息素衰减系数, $\Delta {\tau _{ij}}\left(t \right) = \left\{ {\begin{array}{*{20}{l}} {Q/M, {X_j} \in {C_i}}\\ {0, {\rm{otherwise}}} \end{array}} \right.$, $M = \sum\limits_{i = 1}^k {\sum\limits_{{X_j} \in {C_i}} {d\left({{x_j}, {c_i}} \right)} } $, Q为常数.d(xj, ci)表示样本数据xj与聚类中心ci之间的欧式距离, 定义为
| $d\left( {{x_j},{c_i}} \right) = {\left\| {{x_j} - {c_i}} \right\|_2} = {\left\{ {\sum\limits_{i = 1}^k {{{\left| {{x_{jl}} - {c_{il}}} \right|}^2}} } \right\}^{1/2}}.$ | (2) |
样本数据xj转换到聚类中心ci所代表的类的概率为
| ${P_{ij}}\left( t \right) = \frac{{\tau _{ij}^\alpha \left( t \right)\eta _{ij}^\beta \left( t \right)}}{{\sum\limits_{s = 1}^j {\tau _{sj}^\alpha \left( t \right)\eta _{sj}^\beta \left( t \right)} }},$ | (3) |
其中, ηij是d(xj, ci)的倒数.α, β为参数, 分别表示聚类过程中所更新的τij以及ηij对路径选择的影响作用的大小.如果Pij(t)大于阈值P0, 就将xj合并到ci所在类别中.式(3) 中, Ci表示所有归并到ci邻域的数据集合.求出理想的聚类中心为
| ${c_i} = \frac{1}{l}\sum\limits_{k = 1}^l {{x_k}} ,{x_k} \in {C_i}.$ | (4) |
基于蚁群觅食行为的蚁群算法基本步骤见文献[18].
2 改进K-均值聚类算法 2.1 K-均值聚类算法K-均值聚类算法的相似度是通过待分析数据集中对象两两之间的欧式距离来度量, 聚类数目k是事先确定的, 初始聚类中心是随机选择的, 按最小距离原则将各数据对象分配到k类中的某一类中, 然后重新计算每个类的聚类中心, 最终使得聚类准则函数收敛.准则函数定义为
| $J\left( {X,C} \right) = \sum\limits_{i = 1}^k {\sum\limits_{{x_j} \in sj} {d\left( {{x_j},{c_i}} \right)} } .$ | (5) |
其中:sj代表第i个类别中样本数据的集合, ci是sj内所有样本数据xi的聚类中心, d(xj, ci)表示数据xj与聚类中心ci之间的欧式距离.
2.2 改进后的聚类算法K-均值聚类算法属于梯度下降算法, 使得聚类中心{ci}的很多邻居不能被选择, 使得算法的收敛速度加快, 但在众多没有被选择的邻居中可能存在比当前值更优的解, 使得算法容易陷入局部极值.为了提高解的多样性, 从而跳出局部最优, 从以下两个方面进行改进.
(1) 利用蚁群聚类算法搜寻到初始聚类中心, 随后对于K-均值聚类算法迭代过程中寻找聚类中心计算步骤如下:
(Ⅰ)将数据集中的一个数据按距离最小原则分配给距离其最近的聚类中心所在的类中, 形成新的集合Cm, (m=1, 2,…,k);
(Ⅱ)以集合Cm中所有对象的均值作为新的聚类中心, 返回(Ⅰ), 直至遍历数据集中每一个数据.
(2) 考虑在准则函数上加入一个扰动因子ρ, 即
| $J\left( {X,C} \right) = \sum\limits_{i = 1}^k {\sum\limits_{{x_j} \in sj} {d\left( {{x_j},{c_i}} \right) + \rho } } .$ | (6) |
其中, 扰动因子ρ可以看成给搜索空间中增加一组递减的噪声, 即ρ∈U(-r, r), 用来保持搜索空间的多样性, 扩大局部搜索范围, 从而降低大量局部极小值点对K-均值聚类算法的影响, 提高聚类效果.
基于扰动因子的准则函数下的聚类算法的基本步骤:
(1) 确定聚类数目k, 利用基于蚁群觅食行为的聚类算法寻找k个初始聚类中心;
(2) 将数据集中的数据分别按距离最小原则分配给距离其最近的聚类中心所在的类中, 形成集合Cm, (m=1, 2,…,k);
(3) 以集合Cm中所有对象的均值作为新的聚类中心, 返回(2), 直至遍历数据集中每一个数据;
(4) 以式(6) 作为聚类准则函数, 若聚类准则函数收敛, 算法结束, 否则返回(2).
2.3 时间复杂度分析如果采用随机选择方法产生改进后的K-均值聚类算法的初始聚类中心的集合, 该步骤时间复杂度为O(k).步骤(2)~(3) 采用2.2节中介绍的生成新的聚类的方法以及计算新的聚类中心的方法时间复杂度记为O(2n).步骤(4) 计算公式(6) 规定的聚类准则函数的时间复杂度为O(1), 整个过程需要迭代t次, 所以该算法总的时间复杂度为O(t(k+2n+1)), 而K-均值聚类算法的时间复杂度为O(knt).可以看出, 就时间复杂度而言, 随着聚类数目k或数据集数据的总数n的增加, 改进后的K-均值聚类算法的优势会越来越明显.
3 实验仿真为验证基于蚁群算法的改进K-均值聚类算法的有效性, 采用UCI数据库中的Iris数据进行聚类分析, Iris数据是鸢尾植物数据库, 它主要分布在3种不同类别的鸢尾花, 即山鸢尾、变色鸢尾和维吉尼亚鸢尾, 每一类各占50个样本, 即n=150, 每个数据有4个属性.为了更好地说明实验效果, 采用文献[11]中的方法对Iris数据降维.该方法利用SPSS软件对这4个属性进行相关性分析, 当选取2个主成分时, 提取的信息量为原来的95.801%, 以这2个主成分作为2个属性形成新数据并记为PIris.聚类数目k取定为3, 扰动因子为逐渐递减的均匀分布的随机数, 在Matlab R2014a编程实现.
连续运行100次实验, 对比蚁群聚类算法、经典K-均值聚类算法和本文算法的实验结果, 限于篇幅, 本文提取前5次实验结果, 见表 1.
| 实验次数 | 蚁群聚类算法 | K-均值聚类算法 | 改进后的聚类算法 | |||
| 误差平方和 | 准确率/% | 误差平方和 | 准确率/% | 误差平方和 | 准确率/% | |
| 第1次 | 0.126 3 | 80.0 | 0.169 8 | 80.7 | 0.094 9 | 80.0 |
| 第2次 | 0.459 9 | 65.3 | 0.395 3 | 72.7 | 0.180 0 | 75.3 |
| 第3次 | 0.283 9 | 70.7 | 0.148 0 | 81.3 | 0.092 0 | 82.7 |
| 第4次 | 0.170 9 | 75.5 | 0.451 8 | 72.0 | 0.094 4 | 81.3 |
| 第5次 | 0.124 3 | 80.0 | 0.179 8 | 72.0 | 0.094 4 | 82.7 |
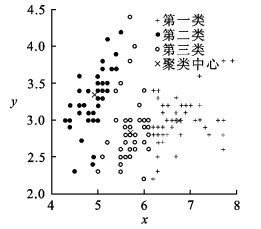
以第一维的数据为x轴, 第二维数据为y轴描点画图.图 1是蚁群聚类算法其中一次最好的聚类结果, 准确率为80.0%, 图 2是经典K-均值聚类算法其中一次最好的聚类结果, 准确率为81.3%, 图 3是改进算法其中一次最好的聚类结果, 准确率为82.7%.由于这3种聚类算法的初始聚类中心是随机选择的, 所以3个类所在的位置也是随机分布的.
|
| 图 1 蚁群聚类算法 Fig.1 Ant colony clustering algorithm |
|
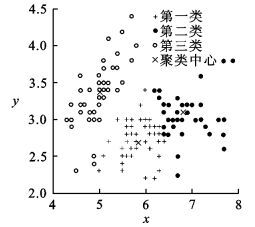
| 图 2 K-均值聚类算法 Fig.2 K-Means clustering algorithm |

|
| 图 3 改进后的聚类算法 Fig.3 The improved clustering algorithm |
连续运行100次实验, 各个聚类算法的平均准确率以及最终的聚类中心和实际的聚类中心的总的误差平方和见表 2.
| 指标 | 蚁群聚类算法 | K-均值聚类算法 | 改进后的聚类算法 |
| 平均准确率/% | 68.13 | 77.9 | 80.67 |
| 总误差平方和 | 53.594 5 | 31.233 | 11.289 |
由表 2可知, 基于蚁群觅食行为的聚类算法的最好结果的准确率为80.0%, K-均值聚类算法的最好结果的准确率为81.3%, 而改进后的聚类算法最好结果的准确率为82.7%, 比K-均值聚类算法的最好结果高1.4%, 比基于蚁群觅食行为的聚类算法的最好结果高3.3%;改进后的聚类算法最差的结果比K-均值聚类算法的最差结果高3.3%, 比基于蚁群觅食行为的聚类算法的最差的结果要高10%.
经过统计, 图 1中有8个属于第一类却被误分到第三类的数据,有5个属于第二类的却被误分到第三类的数据, 有12个属于第三类却被误分到第二类的数据, 有5个属于第三类却被误分第一类的数据, 所以基于蚁群觅食行为的聚类算法的准确率为80.0%;图 2中有6个属于第一类却被误分给第二类的数据, 有5个属于第二类却被误分给第三类的数据, 有12个属于第三类误分给了第二类的数据, 有5个属于第三类却被误分给第一类的数据, 所以经典K-均值聚类算法的准确率为81.3%;图 3中有6个属于第一类误分给第二类的数据, 有3个属于第二类却被误分给第三类的数据, 有12个属于第三类却误分给第二类的数据, 有5个属于第一类却误分给第一类的数据, 所以改进后的聚类算法的准确率为82.7%.
由表 2可知, 连续100次实验后, 蚁群聚类算法的平均准确率为68.13%, K-均值聚类算法的准确率为77.9%, 改进后的聚类算法的平均准确率为80.67%, 比基于蚁群聚类算法的平均准确率高12.54%, 比K-均值聚类算法的准确率要高2.77%.通过计算得到基于蚁群觅食行为的聚类算法得到的聚类中心和实际的聚类中心的误差平方和的总和为53.594 5, K-均值聚类算法得到的聚类中心和实际的聚类中心的误差平方和的总和为31.233, 基于扰动因子的准则函数下的聚类算法得到的聚类中心和实际的聚类中心的误差平方和的总和为11.289, 由此可见, 基于扰动因子的准则函数下的聚类算法得到的聚类中心更接近于实际的聚类中心, 该算法更加稳定, 精确度更高.
4 结束语针对K-均值聚类算法容易陷入局部最优的缺点, 提出基于扰动因子的准则函数下的K-均值聚类算法.通过实验对比基于蚁群觅食行为的聚类算法、K-均值聚类算法和基于扰动因子的相似度下的聚类算法.结果表明, 基于扰动因子的准则函数下的聚类算法能够有效地克服K-均值聚类算法存在的缺点, 提高了聚类效果, 加快了收敛速度.
| [1] | HAN J, KAMBER M. Data mining:Concepts and techniques[M]. San Diego: Morgan Kaufmann Publishers, 2001: 223. |
| [2] | DAVIDSON I, SATYANARAYANA A. Speeding up K-Means clustering using bootstrap averaging[C]//Proc IEEE ICDM 2003 Workshop on Clustering Large Data Sets, Melbourne, FL, 2003:16-25. |
| [3] | JAIN A K, MURTY M N, FLYNN P J. Data clustering:A review[J]. ACM Computing Surveys, 1999, 31(3): 264-323 DOI:10.1145/331499.331504 |
| [4] |
周鲜成, 申群太, 王俊年. 基于微粒群的K均值聚类算法在图像分类中的应用[J].
小型微型计算机系统, 2008, 2(2): 333-336 ZHOU Xiancheng, SHEN Quntai, WANG Junnian. Application of K-means clustering algorithm based on particle swarm optimization in image classification[J]. Journal of Chinese Computer Systems, 2008, 2(2): 333-336 |
| [5] |
陈小全, 张继红. 基于改进粒子群算法的聚类算法[J].
计算机研究与发展, 2012, 49(S): 287-291 CHEN Xiaoquan, ZHANG Jihong. Clustering algorithm based on improved particle swarm optimization[J]. Journal of Computer Research and Development, 2012, 49(S): 287-291 |
| [6] |
朱书伟, 周治平, 张道文. 融合并行混沌萤火虫算法的K-调和均值聚类[J].
智能系统学报, 2015, 35(3): 685-690 ZHU Shuwei, ZHOU Zhiping, ZHANG Daowen. K-harmonic means clustering merged with parallel chaotic firefly algorithm[J]. CAAI Transactions on Intelligent Systems, 2015, 35(3): 685-690 |
| [7] |
王伟, 刘付显. 基于混沌粒子群K-均值算法的人员分类训练[J].
军事运筹与系统工程, 2015, 29(3): 10-15 WANG Wei, LIU Fuxian. Based on chaos particle swarm K-means algorithm classification of personnel training[J]. Military Operations Research and Systems Engineering, 2015, 29(3): 10-15 |
| [8] |
朱书伟, 周治平, 张道文. 基于改进多目标萤火虫算法的模糊聚类[J].
计算机应用, 2015, 35(3): 685-690 ZHU Shuwei, ZHOU Zhiping, ZHANG Daowen. Improved multi-objective firefly algorithm-based fuzzy clustering[J]. Journal of Computer Applications, 2015, 35(3): 685-690 DOI:10.11772/j.issn.1001-9081.2015.03.685 |
| [9] |
叶志伟, 尹宇洁, 王明威, 等. 一种基于杜鹃搜索算法的聚类分析方法[J].
微电子学与计算机, 2015, 32(5): 105-110 YE Zhiwei, YIN Yujie, WANG Mingwei, et al. A clustering approach based on cuckoo search algorithm[J]. Microelectronics & Computer, 2015, 32(5): 105-110 |
| [10] |
满扬, 王晓东. 基于扰动因子的相似度下的聚类算法[J].
西安工程大学学报, 2016, 30(2): 280-283 MAN Yang, WANG Xiaodong. Clustering algorithm under the similarity based on the disturbance factor[J]. Journal of Xi'an Polytechnic University, 2016, 30(2): 280-283 |
| [11] |
王凡, 贺兴时, 王燕. 基于高斯扰动的布谷鸟搜索算法[J].
西安工程大学学报, 2011, 25(4): 566-569 WANG Fan, HE Xingshi, WANG Yan. The cuckoo search algorithm based on gaussian disturbance[J]. Journal of Xi'an Polytechnic University, 2011, 25(4): 566-569 |
| [12] |
张毅, 贺兴时, 杨新社. 基于模拟退火与高斯扰动的布谷鸟算法[J].
纺织高校基础科学学报, 2015, 28(4): 515-521 ZHANG Yi, HE Xingshi, YANG Xinshe. A cuckoo search algorithm based on simulated annealing and gaussian disturbance[J]. Basic Sciences Journal of Textile Universities, 2015, 28(4): 515-521 |
| [13] |
张伟. 基于随机搜索变异策略的人工蜂群算法[J].
纺织高校基础科学学报, 2014, 27(4): 512-517 ZHANG Wei. Random mutation artificial bee colony algorithm[J]. Basic Sciences Journal of Textile Universities, 2014, 27(4): 512-517 |
| [14] |
刘召军, 高兴宝. 融合自适应混沌差分进化的粒子群优化算法[J].
纺织高校基础科学学报, 2015, 28(1): 116-123 LIU Zhaojun, GAO Xingbao. Particle swarm optimization algorithm by integrating adaptive chaos differential evolution[J]. Basic Sciences Journal of Textile Universities, 2015, 28(1): 116-123 |
| [15] | LU Qiang. K-means optional clustering algorithm based an hybrid genetic technique[J]. Journal of East China University of Science and Technology, 2005, 31(2): 218-222 |
| [16] | SHELOKARPS, JAYARAMANVK, KULKAMI B D. An ant colony approach for clustering[J]. Analytica Chimica Acta, 2004, 509(2): 187-195 DOI:10.1016/j.aca.2003.12.032 |
| [17] | DORIGOM, MANIEZZO V, COLORNI A. Ant system:Optimization by a colony of cooperating agents[J]. IEEE Trans on Systems, Man, and Cybernetics Part B, 1996, 26(1): 29-41 DOI:10.1109/3477.484436 |
| [18] |
贾瑞玉, 王会颖. 基于改进蚁群算法的聚类分析[J].
计算机应用与软件, 2010, 27(12): 97-100 JIA Ruiyu, WANG Huiying. Cluster analysis based on improved ant colony algorithm[J]. Computer Applications and Software, 2010, 27(12): 97-100 DOI:10.3969/j.issn.1000-386X.2010.12.031 |



