0 引 言

动力学网络是自然科学领域的重要研究课题.很多自然现象可由动力学网络的同步来解释,因而动力学网络同步得到各领域专家和学者的深入研究^{[1, 2]}.实际中，网络受到各种不同的外界因素影响,各节点间很难自发地达到同步.为了实现网络各节点间的同步,学者们提出了一些控制方法. 文献^[3]讨论了牵制控制方法. 选取部分节点加以控制就可实现整个网络的同步,因此牵制控制是一种很好的动力学网络同步的控制方法. 然而,在网络结构未知时控制节点的选定还是一个未解决的问题,并且该控制方法要求网络的各节点必须完全相同.

另一方面,网络同步的全节点控制方法也得到了一定的研究. 由于脉冲控制的结构简单,文献^{[4, 5]}讨论了结构未知的动力学同步的脉冲控制方法. 由于自适应控制的自动化、反应快速等优点,文献^[6]讨论了动力学网络同步的自适应控制方法. 然而,这些控制方法都是以节点系统的一个解为控制目标轨道. 当节点系统的解无法获得不是稳定的同步流形时,这些控制方法或不能应用. 文献^[7]以节点状态的平均为目标轨道,设计了网络的同步方法来解决上述问题,并且该方法也适用于有参数失配的动力学网络. 基于节点状态的加权平均,文献^[8]设计了实现网络同步的脉冲控制方案. 本文以节点状态的加权平均为目标轨道,设计实现有参数失配的动力学网络同步的自适应控制方法,并通过理论分析该方法的有效性.

1 自适应同步方案及理论分析

考虑由m个节点构成的动力学网络

$\dot{x}$i=F(xi,pi)+gi(x1,x2,…,xm),i=1,2,…,m,

(1)

其中xⁱ=(x₁ⁱ,x₂ⁱ,…,x_nⁱ)^T是第i个节点的状态向量,gⁱ(x¹,x²,…,x^m)是网络的未知耦合函数,F(x,pⁱ)=(F₁(x,pⁱ),F₂(x,pⁱ),…,F_n(x,pⁱ))^T是描述第i个节点的动力学的向量函数,且具有下列形式:

Fk(x,pi)=ck(x)+$\sum\limits_{j=1}^{l}{{}}$pkji fkj(x),i=1,2,…,m,k=1,2,…,n.

(2)

其中c_k(x)和f_kj (x)是线性或非线性函数. n×l阶矩阵pⁱ=(p_kjⁱ)_n×l是节点系统的未知参数.

在每个节点加上控制器uⁱ=(u₁,u₂,…,u_n)^T,则受控的网络为

${\dot{x}}$i=F(xi,pi)+gi(x1,x2,…,xm)+ui.

(3)

文献^[9]利用节点状态的加权平均X(t)=$\sum\limits_{i=1}^{m}{{}}$ξⁱxⁱξⁱ≥0,$\sum\limits_{i=1}^{m}{{}}$ξⁱ=1提出了研究网络同步的稳定性的一种新方法. 本文以X(t)=$\sum\limits_{i=1}^{m}{{}}$ξⁱxⁱξⁱ≥0,$\sum\limits_{i=1}^{m}{{}}$ξⁱ=1为同步目标轨道,设计网络同步的自适应控制方法. 显然,X(t)满足方程

${\dot{X}}$(t)=$\sum\limits_{i=1}^{m}{{}}$[ξiF(xi,pi)+ξigi(x1,x2,…,xm)+ξiui].

(4)

定义同步误差

δxi=xi-x(t),i=1,2,…,m.

(5)

显然,同步误差服从方程

δ${\dot{x}}$i=f(xi,pi)+gi(x1,x2,…,xm)+ui-G(x),i=1,2,…,m.

(6)

其中向量函数G(x)为

G(x)=$\sum\limits_{i=1}^{m}{{}}$[ξiF(xi,pi)+ξigi(x1,x2,…,xm)+ξiui].

(7)

注意到同步误差满足

$\sum\limits_{i=1}^{m}{{}}$ξiδxi=0.

(8)

本文的目标是设计控制器uⁱ(i=1,2,…,m)使系统(6)在原点稳定. 受文献^{[7, 8, 9, 10, 11, 12]}启发,引入如下自适应反馈控制器

uki=εk(xki-Xk(t))-$\sum\limits_{j=1}^{l}{{}}$=1qkji fkj(X(t)),i=1,2,…,m,k=1,2,…,n.

(9)

其中q_kjⁱ 和 ε_k 常称为反馈控制强度,按如下规律更新:

${\dot{\varepsilon }}$k=-γk$\frac{1}{m}$$\sum\limits_{i=1}^{m}{{}}$(xki-Xk(t))2,k=1,2,…,n,

(10)

${\dot{q}}$kji=σkj (xki-Xk(t))fkj(X(t)),i=1,2,…,m,k=1,2,…,n,j=1,2,…,l,

(11)

其中γ_k和σ_kj 是正常数.

由方程(11)得

$\sum\limits_{i=1}^{m}{{}}$ξi${\dot{q}}$kji=σkj fkj(X(t))$\sum\limits_{i=1}^{m}{{}}$ξi(xki-Xk(t))=0.

(12)

则$\sum\limits_{i=1}^{m}{{}}$ξⁱq_kjⁱ 是由初值确定的常数. 若选取初值q_kjⁱ=0,则$\sum\limits_{i=1}^{m}{{}}$ξⁱq_kjⁱ 将恒为零.

基于网络各节点状态的平均值X(t)=$\sum\limits_{i=1}^{m}{{}}$$\frac{{{x}^{i}}}{m}$,文献^[7]设计了实现有参数失配的动力学网络同步的自适应控制方法,并且每个节点都采用不同的自适应控制强度. 这就要求为每个节点增加一个n维的系统来计算控制强度ε,并且每个节点都需要把状态信息发送给网络其他所有节点. 本文方法的优点在于所有的节点采用相同的反馈强度ε,因此对整个网络只需增加一个n维系统来计算ε,降低了控制系统的维数. 利用X(t)=$\sum\limits_{i=1}^{m}{{}}$ξⁱxⁱξⁱ≥0,$\sum\limits_{i=1}^{m}{{}}$ξⁱ=1.作为目标控制轨道. ξⁱ≥0，令某个 ξⁱ=1,其他所有ξⁱ=0. 在这种情况下,只有节点i需要将自己的状态信息发给其他节点,降低了控制过程中的信号传递量.

为分析控制方法的有效性,给出如下假设.

假设1 假设动力学网络(3)是有界的. 令Ω₁⊂Rⁿ和Ω₂⊂R^mn是2个有界集,并对x₁,x₂∈Ω₁和y₁,y₂∈Ω₂,存在正常数l₁,l₂,使得

‖F(x1,pi)-F(x2,pi)‖≤l1‖x1-x2‖,

(13)

‖g(y1)-g(y2)‖≤l2‖y1-y2‖.

(14)

假设2  ∀x¹=x²=…=x^m=x∈Rⁿ,耦合函数gⁱ(x¹,x²,…,x^m)满足

g1(x,x,…,x)=g2(x,x,…,x)=…=gm(x,x,…,x).

(15)

条件(13),(14)为一般性的李普希兹条件. 条件(15)为确保存在稳定的同步流形.在先前的研究中要求gⁱ(x,x,…,x)=0或gⁱ(x,x,…,x)+uⁱ=0,因此同步目标轨道一定是节点系统的一个解. 由条件(15)知,本文的方法不需要同步目标轨道是节点系统的一个解.

为证明式(3),(9)～(11)构成的系统达到同步,引入如下非负函数

V(δxi)=$\frac{1}{2}\sum\limits_{i=1}^{m}{{}}\delta {{x}^{{{i}^{T}}}}\delta {{x}^{i}}+\frac{m}{2}\sum\limits_{i=1}^{m}{{}}\frac{1}{{{\gamma }_{k}}}{{\left( {{\varepsilon }_{k}}+L \right)}^{2}}+\frac{1}{2}\sum\limits_{i=1}^{m}{{}}\sum\limits_{k=1}^{n}{{}}\sum\limits_{j=1}^{l}{{}}\frac{1}{{{\sigma }_{kj}}}{{\left( q_{kj}^{i}-p_{kj}^{i}+\sum\limits_{h=1}^{m}{{}}{{\xi }^{h}}p_{kj}^{h} \right)}^{2}},$

其中L为可选择的常数.对V求微分,并利用式(8)得

${\dot{V}}$=$\sum\limits_{i=1}^{m}{{}}$[δxiTF(xi,pi)+δxiTgi(x1,x2,…,xm)]- $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxi[F(xh,ph)+gh(x1,x2,…,xm)]+ $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{k=1}^{n}{{}}$δxki$\sum\limits_{h=1}^{m}{{}}$ξh$\sum\limits_{j=1}^{l}{{}}$qkjh fkj(X(t))+ $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{k=1}^{n}{{}}$$\sum\limits_{j=1}^{l}{{}}$-pkji+$\sum\limits_{h=1}^{m}{{}}$ξhpkjh δxki fkj(X(t))-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{n}{{}}$Lδxki2.

(16)

式(16)中

$\sum\limits_{i=1}^{m}{{}}$δxiTF(xi,pi)-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxiF(xh,ph)= $\sum\limits_{i=1}^{m}{{}}$δxiT[F(xi,pi)-F(X(t),pi)]-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxi[F(xh,ph)-F(X(t),ph)]+ $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{k=1}^{n}{{}}$$\sum\limits_{j=1}^{l}{{}}$pkji-$\sum\limits_{h=1}^{m}{{}}$ξhpkjh δxkifkj(X(t)),

(17)

及

$\sum\limits_{i=1}^{m}{{}}$δxiTgi(x1,x2,…,xm)-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxigh(x1,x2,…,xm)= $\sum\limits_{i=1}^{m}{{}}$δxiT[gi(x1,x2,…,xm)-gi(X(t),X(t),…,X(t))]- $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxi[gh(x1,x2,…,xm)-gh(X(t),X(t),…,X(t))].

(18)

将式(17)~(18)带入式(16)得

${\dot{V}}$=$\sum\limits_{i=1}^{m}{{}}$δxiT[F(xi,pi)-F(X(t),pi)]-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{m}{{}}$ξhδxi[F(xh,ph)-F(X(t),ph)]+ $\sum\limits_{i=1}^{m}{{}}$δxiT[gi(x1,x2,…,xm)-gi(X(t),X(t),…,X(t))]- $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{m}{{}}$ξhδxi[gh(x1,x2,…,xm)-gh(X(t),X(t),…,X(t))]+ $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{k=1}^{n}{{}}$δxki$\sum\limits_{h=1}^{m}{{}}$ξh$\sum\limits_{j=1}^{l}{{}}$qkjh fkj(X(t)) -$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{m}{{}}$Lδxi2k.

若初始条件为q_kjⁱ=0,利用等式(12),得

${\dot{V}}$=$\sum\limits_{i=1}^{m}{{}}$δxiT[F(xi,pi)-F(X(t),pi)]-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{h=1}^{m}{{}}$ξhδxi[F(xh,ph)-F(X(t),ph)]+ $\sum\limits_{i=1}^{m}{{}}$δxiT[gi(x1,x2,…,xm)-gi(X(t),X(t),…,X(t))]- $\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{m}{{}}$ξhδxi[gh(x1,x2,…,xm)-gh(X(t),X(t),…,X(t))]-$\sum\limits_{i=1}^{m}{{}}$$\sum\limits_{j=1}^{m}{{}}$Lδxi2k.

利用假设1和假设2,得

${\dot{V}}$≤(1+m)l1$\sum\limits_{i=1}^{m}{{}}$‖δxi‖2+(1+m)l2$\sum\limits_{i=1}^{m}{{}}$‖δxi‖2-L$\sum\limits_{i=1}^{m}{{}}$‖δxi‖2.

显然,若L足够大,${\dot{V}}$≤0,并且 ${\dot{V}}$=0当且仅当δx_kⁱ=0.利用微分方程的稳定性理论,当t→+∞时,δxⁱ →0,且ε,qⁱ趋于常数,若δ_kⁱ和ε的初值任意选取,q_klⁱ 的初值选为零.

2 数值算例

为表述方便，引入如下标量

ej(t)=1m$\sum\limits_{i=1}^{m}{{}}$|δxji |,j=1,2,…,n.

显然,当t→∞时,若e_j(t)趋于零,则δx_jⁱ趋于零. 在下文统一混沌系统的例子中,令节点数m=100,耦合函数为

gki(x1,x2,…,xkm)=1m$\sum\limits_{j=1}^{m}{{}}$bijsin(xj),i=1,2,…,m.

其中(b_ij)_m×m是随机选取的,b_ij=1(i≠j)的概率为0.5,且b_ii=$-\sum\limits_{i\ne j}^{{}}{{}}{{b}_{ij}}$-1.

统一混沌系统可描述为

${\dot{x}}$1=-(25α+10)(x1-x2), ${\dot{x}}$2=-x1 x3+(28-35α)x1+(29α-1)x2, ${\dot{x}}$3=x1 x2-$\frac{\alpha +8}{3}$x3.

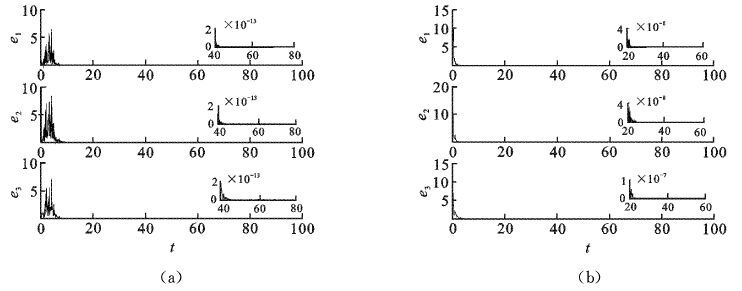
其中α为[0,1]上变化的参数^{[13, 14]}. 考虑到参数失配,令第i个节点的系统参数为αⁱ=α+ηⁱ,其中ηⁱ随机的从[-0.05,0.05]上选取. 在数值模拟中,令σ_k=0.1,γ_k=0.1,q_kⁱ和ε_k为零,且x_kⁱ在 [1,-1]随机选取. 相应的数值结果见图 1.在图 1(a)中,令参数α=0.3,ξ₁=1,ξ_i=0(i≠1);在图 1(b)中,令参数α=0.3,ξ_i=0.05(i=1,…,20),ξ_i=0(i=21,…,100).结果表明随时间同步误差趋于零,网络的各节点达到同步.

3 结束语

基于网络节点状态的加权平均,设计了实现有参数失配的动力学网络同步的自适应控制方法,并基于微分方程的稳定性理论分析了方法的有效性. 与先前以节点系统的解为控制目标轨道的控制方法相比,该方法适用于有参数失配的动力学网络,且同步目标轨道不必是节点系统的解. 与先前以节点状态的平均值为同步目标轨道的同步方法相比,该控制方法的控制系统结构更加简单,且控制过程中信息的传递量更小.文中网络的每个节点是由一般的常微分方程描述,实际中节点可由其他类型方程来描述,如分数阶系统. 将此方法推广到这类网络系统还有待进一步研究.