2. 密德萨斯大学 科学与技术学院, 英国 伦敦 NW4 4BT
2. School of Science & Technology, Middlesex University, London NW4 4BT UK
蝙蝠算法(bat algorithm, 简称BA) 是英国学者YANG Xinshe于2010年提出的一种基于蝙蝠回声定位行为的新型启发式算法[1].自提出以来, 蝙蝠算法被广泛应用于各类优化问题.盛孟龙等提出一种改进的自适应变异蝙蝠算法[2], 引入交叉变换的方式更新蝙蝠群体的位置; 刘长平等提出基于Levy飞行特征的蝙蝠算法[3], 采用Levy飞行搜索策略,更为真实地模拟蝙蝠的捕食行为, 充分利用不均匀随机游走的特性, 有效避免了局部极值的吸引; 贺兴时等将模拟退火的思想引入BA算法中, 同时对某些个体进行高斯扰动, 提出了一种基于模拟退火的高斯扰动蝙蝠优化算法[4]; SELIM Yilmaz等人对算法更新模式进行改进, 并将其应用于连续优化问题[5]中.
在蝙蝠算法的应用方面, YANG将BA运用于多目标优化[6]的工程设计; 李枝勇等将遗传变异蝙蝠算法应用0-1背包问题[7]; GANDOMI等将BA运用于分类问题[8]; MISHRA S等将BA运用于模糊聚类[9]; KHAN K等将BA运用于预测问题[10]和神经网络[11].蝙蝠算法的收敛性证明方面, 也少有文献涉及.黄光球等构造了可全局收敛的蝙蝠算法[12], 用于求解大规模优化问题; 李枝勇等定义了两种新的蝙蝠算法的更新模式[13], 分别对这两种模式进行收敛性分析.丁文静等在模拟退火的高斯扰动蝙蝠优化算法的基础上, 探讨了基于动态加权和向量估计的改进方法, 并将改进后的蝙蝠算法应用于多目标优化[14]; 肖辉辉等提出一种基于差分进化算法的改进蝙蝠算法[15], 并将其应用于求解数值积分问题; 盛晓华等利用对蝙蝠算法重新编码以及初始化的方式来求解离散型生产调度问题[16]; 张勇凯等对蝙蝠算法进行混沌序列初始化和自适应变步长的改进[17], 运用于云制造平台中, 效果较好; 于泉等提出蝙蝠-拟牛顿混合算法[18], 将其成功应用于无线传感器网络节点定位.然而, 基本的蝙蝠算法存在容易陷入局部最优,过早进入停滞状态等问题.为了更好地控制蝙蝠算法的开发和探索能力, 解决基本蝙蝠算法的缺点, 文中在蝙蝠算法更新模式中引入时变的惯性权重, 给出3种不同的惯性权重学习机制, 将蝙蝠算法进行改进.通过数值仿真实验, 将3种不同学习机制下的改进蝙蝠算法与基本算法进行对比分析.
1 基本蝙蝠算法蝙蝠在捕猎时, 利用声呐探测猎物、避免障碍物, 这些行为都依赖于回声定位的声学原理.BA便是受启于蝙蝠的生物行为, 从而得出的一种基于种群的随机全局优化技术.蝙蝠通过发出声音脉冲, 然后根据其回声定位器接收到的回声来探测猎物的位置, 绕开障碍物, 在黑暗中栖息.蝙蝠发出声音的响度范围从搜索猎物时的最高响度到靠近猎物时的静音.蝙蝠个体通过发出和接收回声的时间差, 判断目标的距离、方位.
在一个d维搜索空间中, 第i只蝙蝠在t时刻的位置为xit, 速度为vit, 更新公式为
| ${f_i} = {f_{\min }} + \left( {{f_{\max }}-{f_{\min }}} \right)\beta, $ | (1) |
| $v_i^{t + 1} = w{v_i}^\prime + \left( {p-{x_i}^\prime } \right){f_i}, $ | (2) |
| $x_i^{t + 1} = x_i^t + v_i^t$ | (3) |
式中,fi, fmax, fmin分别表示第i只蝙蝠当前时刻发出的声波频率以及声波频率的最大值和最小值;w表示速度更新中的惯性权重;β∈[0, 1]为一个随机向量;p表示当前最优位置.开始时每只蝙蝠随机分配频率, 频率从[fmin, fmax]随机得出.
2 改进学习机制的蝙蝠算法 2.1 时变惯性权重惯性权重w作为蝙蝠算法中为数不多的参数之一, 有着很重要的作用, 惯性权重的大小决定了对前一个蝙蝠个体速度继承的多少.一般地, 惯性权重主要有固定权重和时变权重两种选择.固定权重是在算法迭代过程中, 固定地选择某一个常数作为权重值, 在整个优化过程中不做变动.时变权重是随着迭代次数的增加, 惯性权重取值也不断变化.在整个迭代过程中按照某种递减率减小, 从而呈现出不同的取值情况.较大的惯性权重将使蝙蝠个体具有较大的速度, 从而增强了蝙蝠的探索能力; 较小的惯性权重将使蝙蝠个体具有较强的开发能力.因此, 算法的优化效果很大程度上取决于惯性权重的选取, 并且时变的惯性权重更有利于增加算法多样性, 提高搜索能力和探索能力.文中提出3种不同方案的递减性时变惯性权重学习机制, 即
| $\left\{ \begin{array}{l} {w_1} = {w_{\max }}\left( {{w_{\max }}-{w_{\min }}} \right)\frac{{{T_{\max }}-k}}{{{T_{\max }}}}, \\ {w_2} = {w_{\max }}-\left( {{w_{\max }} - {w_{\min }}} \right){\left( {\frac{k}{{{T_{\max }}}}} \right)^2}, \\ {w_3} - {w_{\min }}{\left( {\frac{{{w_{\max }}}}{{{w_{\min }}}}} \right)^{\frac{1}{{1 + 10k/T\max }}}} \end{array} \right..$ | (4) |
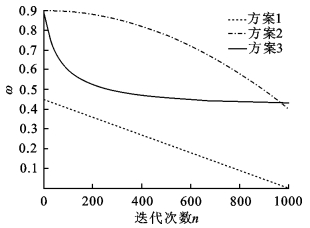
式中,w1, w2, w3分别表示方案1, 2, 3的时变惯性权重表达式; wmax, wmin分别表示惯性权重的最大、最小值, 根据已有的数值实验发现, 当其分别取值为0.9,0.4时, 算法收敛效果较好; Tmax为最大迭代次数, k为当前迭代次数.易知, 这3种学习机制中的惯性权重均是随着迭代次数的增加按照某种递减率逐次减小的, 衰减曲线如图 1所示.其中, 方案1中时变权重w1的衰减性态为简单的一次函数, 方案2中时变权重w2的衰减性态为二次函数, 方案3中时变权重w3的衰减性态为指数函数.
|
| 图 1 时变惯性权重取值情况 Fig.1 Value circumstances of time-varying inertia weight |
根据提出的3种不同的递减性惯性权重学习机制, 基本蝙蝠算法的速度更新公式得到改进, 即
方案1:
| $\left\{ \begin{array}{l} v_i^{t + 1} = {w_1}v_i^t + \left( {p-x_i^t} \right){f_i}, \\ {w_1} = {w_{\max }}\left( {{w_{\max }}-{w_{\min }}} \right)\frac{{{T_{\max }}-k}}{{{T_{\max }}}}. \end{array} \right.$ | (5) |
从式(5) 可以看出, 时变惯性权重w1是以当前迭代次数k为变量, 呈现出简单一次线性的衰减性态.
方案2:
| $\left\{ \begin{array}{l} v_i^{t + 1} = {w_2}v_i^t + \left( {p-x_i^t} \right){f_i}, \\ {w_2} = {w_{\max }}-\left( {{w_{\max }}-{w_{\min }}} \right){\left( {\frac{k}{{{T_{\max }}}}} \right)^2}. \end{array} \right.$ | (6) |
从式(6) 中可以看出, 时变惯性权重w2的衰减性态是以迭代次数为变量的二次函数形式, 衰减后的最小值比w1大得多, 也就是方案2的惯性权重取值对速度有着更大的继承.
方案3:
| $\left\{ \begin{array}{l} v_i^{t + 1} = {w_3}v_i^t + \left( {p-x_i^t} \right){f_i}, \\ {w_3} = {w_{\min }}{\left( {\frac{{{w_{\max }}}}{{{w_{\min }}}}} \right)^{\frac{1}{{1 + 10k/T\max }}}}. \end{array} \right.$ | (7) |
从式(7) 可以看出, 时变惯性权重w3的衰减性态是以迭代次数为变量的指数函数形式, 其衰减速率比w1缓慢得多, 迭代1 000次后的取值与w2相近.
3 仿真实验为验证本文提出的3种具有不同衰减性态的时变惯性权重学习机制的蝙蝠算法性能, 选取4个标准测试函数进行仿真测试, 并与基本进行对比.
3.1 参数设置蝙蝠算法中涉及的参数较少, 参数的选取目前尚无确切的理论依据, 本文所选择的参数值是由反复实验获得的经验值确定.其中, 基本的惯性权重w=0.5, 改进算法wmax=0.9, wmin=0.4, 算法最大搜索次数均为Tmax=1000, 群体数D=30.
3.2 测试函数4种测试函数如表 1所示.测试函数均是非线性函数, 可以有效地检验算法的探索、开发性能.其中, g1函数是典型的单模态函数; g2函数是多峰的, 它的局部最优值随着维数的升高而增加, 能够独立地优化各变量, 有众多局部极值且多个极小值呈规律分布; g3函数由于自身特性,致使算法极易陷于局部极值,是测试算法收敛性能的经典函数;g4函数具有非常粗糙的适应度表面, 很容易诱导进入非真的全局最优解, 从而陷入局部极值中, 是测试算法全局收敛性能的极佳函数.
| 函数名 | 函数表达式 | 维数 | x取值范围 | 最优值 |
| Sphere | 30 | [-100, 100] | 0 | |
| Griewank | 30 | [-600, 600] | 0 | |
| Zakharov | 30 | [-10, 10] | 0 | |
| Schwefel′s problem | 30 | [-500, 500] | 0 |
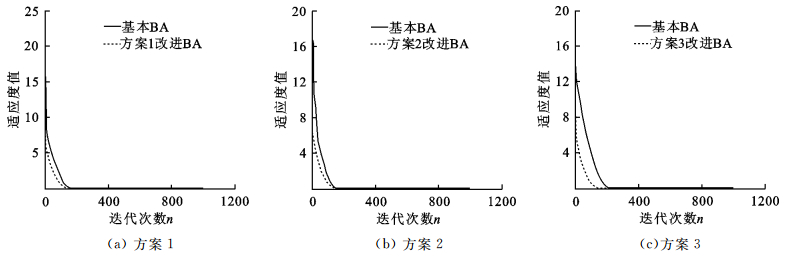
仿真实验规定, 当测试中实际的寻优值与理论最优值的相对误差小于1%时, 视为找到最优解, 规定每种算法独立运行10次.图 2为3种时变惯性权重改进后的蝙蝠算法与基本蝙蝠算法的收敛曲线对比图, 形象地展示了改进前后的蝙蝠算法适应度值的迭代下降过程.
|
| 图 2 测试函数g1的收敛曲线对比图 Fig.2 Convergence curves of testing function g1 |
从图 2(a), (b) 可以看出, 在测试函数g1的仿真实验中, 方案1, 2改进后的蝙蝠算法相对于基本算法的性能均有所提升, 收敛的迭代次数基本持平于150次, 并且在前100次的迭代过程中收敛精度和收敛速度都优于基本蝙蝠算法.从图 2(c)中可以看出, 在对测试函数g1的仿真实验中, 方案3改进蝙蝠算法的收敛性能比基本算法提升很多, 收敛速度明显加快, 基本蝙蝠算法在200次迭代后才收敛, 引入时变惯性权重的改进算法达到最优值所需的迭代次数明显减少.
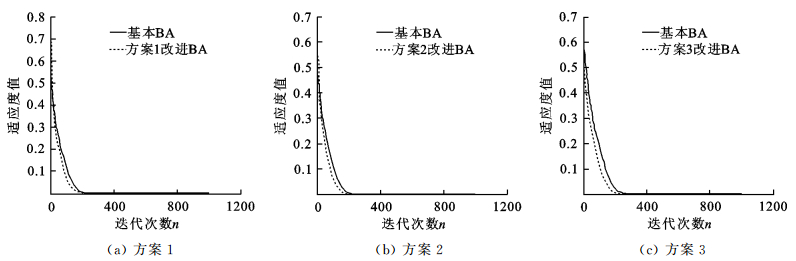
从图 3(a), (b) 中可以看出, 在测试函数g2的仿真实验中, 前两种衰减性态的时变惯性权重改进的蝙蝠算法在收敛速度方面, 作用类似, 但均比基本算法表现更优; 同时, 对测试函数g2来说, 方案2改进的算法达到收敛所需的迭代次数较方案1有所减少;从图 3(c)中可以看出,方案3改进的算法收敛性略差于方案1和方案2,迭代次数较方案2有所增加.
|
| 图 3 测试函数g2的收敛曲线对比图 Fig.3 Convergence curves of testing function g2 |
从图 4(a)~(c)可以看出, 在测试函数g3的仿真实验中, 方案1和方案3改进后的蝙蝠算法性能得到有效的改善.基本蝙蝠算法收敛需要的迭代次数几乎均达到实验允许的最大值1 000次, 而改进后的算法则明显寻优能力更强, 算法收敛到最优值所需要的迭代次数明显减少, 收敛速度提高.从图 4(b)可以看出, 方案2改进后的蝙蝠算法性能和方案1, 方案3比较并不突出, 但是, 算法性能得到提升, 在迭代进行到400次时就达到最优解, 而基本蝙蝠算法则是在进行到800次时才取到最优解.

|
| 图 4 测试函数g3的收敛曲线对比图 Fig.4 Convergence curves of testing function g3 |
从图 5(a), (b)可以看出, 在测试函数g4的仿真实验中, 对方案1, 虽然当迭代次数小于100次时, 基本蝙蝠算法表现更优, 但是基本蝙蝠算法陷入了局部极值, 且最终没有跳出, 方案1改进的蝙蝠算法收敛速度和收敛精度均高于基本算法.对方案2, 在200次迭代之前基本蝙蝠算法的收敛速度快于改进后的算法, 但是同样地在后来的测试过程中基本蝙蝠算法不可避免地陷入了局部极值, 没有收敛到最优解.而方案2改进后的算法在很大程度上提升了算法性能, 收敛精度较高.从图 5(c)可以看出, 在对测试函数g4的仿真实验中, 方案3改进的蝙蝠算法虽然在收敛速度方面优势并不明显, 但它在收敛精度和避免进入局部极值方面均有所改善, 比基本蝙蝠算法表现更优.

|
| 图 5 测试函数g4的收敛曲线对比图 Fig.5 Convergence curves of testing function g4 |
纵观所有的收敛曲线对比图, 可以发现, 引入时变惯性权重的改进蝙蝠算法均比基本算法的性能好, 在一定程度上提高了算法的收敛速度和收敛精度, 在避免进入局部极值方面也比基本算法表现更优.而且对于不同的测试函数, 3种不同衰减性态的时变惯性权重方案对算法收敛性态有着不同的影响, 方案1和方案2的改进效果较为相似.在各个测试函数仿真实验后的收敛速度和收敛精度方面, 方案3的改进效果都优于方案1,2, 并且在惯性权重衰减的过程中, 当权重值递减到0.4~0.5时, 算法的改进效果最优; 如果继续递减, 改进效果则下降, 而方案3中惯性权重最终在这个范围内, 因此可以认定这3种不同的衰减性态中, 方案3的效果最好.
为了进一步测试方案3改进后的BA性能, 将其与另外2种时变惯性权重方案进行对比性的仿真实验.实验结果表明, 本文提出的改进方案效果更优.其中, 进行仿真实验对比的2种改进方案如下.
方案4:
| $\left\{ \begin{array}{l} v_i^{t + 1} = {w_4}v_i^t + \left( {p + {x_i}^\prime } \right){f_i}, \\ {w_4} = {w_{{\rm{end}}}}{\left( {\frac{{{w_{{\rm{start}}}}}}{{{w_{{\rm{end}}}}}}} \right)^{\frac{1}{{1 + ct/T\max }}}}. \end{array} \right.$ | (8) |
方案4的改进方法来自于文献[19], 分别通过4个测试函数将其进行对比仿真, 即将方案3和方案4分别用于4种测试函数, 得到的对比结果如图 6所示.

|
| 图 6 不同测试函数中方案3与方案4对比 Fig.6 Comparison between the scheme 3 and 4 on different testing functions |
从图 6可以看出, 在选用的4个不同的测试函数下, 方案3改进后的BA算法在收敛速度和收敛精度上均比文献[19]中提出的改进方案要好.
方案5:
| $\left\{ \begin{array}{l} v_i^{t + 1} = {w_5}{v_i}^\prime + \left( {p-x_i^t} \right){f_i}, \\ {w_5} = {w_{\min }} + \left( {{w_{\max }}-{w_{\min }}} \right)\left( {\frac{t}{{{T_{\max }}}}} \right). \end{array} \right.$ | (9) |
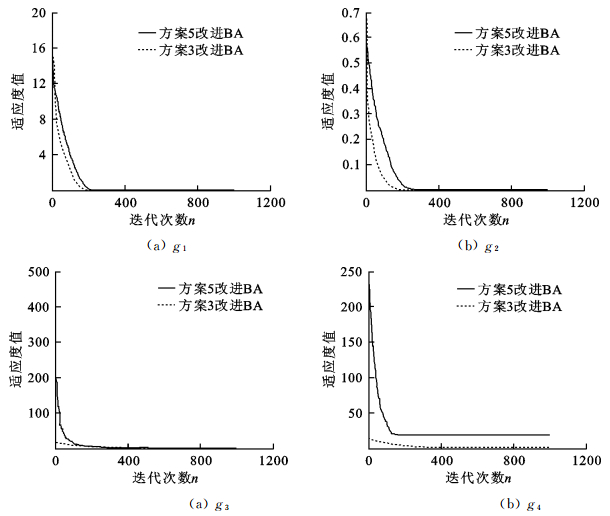
方案5的改进方法来自于文献[20], 同样地, 分别通过4个测试函数将两种方案进行对比仿真实验, 得到的对比结果如图 7所示.
|
| 图 7 不同测试函数中方案3与方案5对比 Fig.7 Comparison between the scheme 3 and the scheme 5 on different testing functions |
从图 7可以看出, 方案3改进的BA算法比文献[20]中提出的改进方案效果要好, 在算法的收敛速度和收敛精度方面, 方案3均表现更优.文中提出的改进方案是切实有效的.
4 结束语本文在基本蝙蝠优化算法的理论基础上, 引入了时变的惯性权重, 用3种不同衰减性态的权重模式将蝙蝠算法进行改进, 并通过标准测试函数进行仿真实验.结果表明, 3种方案改进后的蝙蝠算法均有效改善了算法性能, 增强了收敛速度和精度, 蝙蝠个体的寻优能力得到了提升.
蝙蝠算法自提出以来, 被广泛应用到各类优化问题, 为了提升基本蝙蝠算法性能, 使其能够更好地解决各类问题, 学者们对蝙蝠算法的研究不断深入.算法收敛性方面的解析则是改进算法很重要的突破口, 然而这方面的研究却并不详尽.在未来的研究中, 会在蝙蝠算法的收敛性、鲁棒性等方向做更深入的探索.
| [1] | YANG Xinshe.A new met heuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization, Berlin:Springer-Verlay, 2010:65-74. |
| [2] |
盛孟龙, 贺兴时, 丁文静. 蝙蝠算法的全局收敛性分析[J].
纺织高校基础科学学报, 2013, 26(4): 543-547 SHENG Menglong, HE Xingshi, DING Wenjing. Analysis of bat algorithm's global convergence[J]. Basic Sciences Journal of Textile Universities, 2013, 26(4): 543-547 |
| [3] |
刘长平, 叶春明. 具有Levy飞行特征的蝙蝠算法[J].
智能系统学报, 2013, 8(3): 240-246 LIU Changping, YE Chunming. Bat algorithm with the characteristics of Levy flights[J]. CAAI Transactions on Intelligent Systems, 2013, 8(3): 240-246 |
| [4] | HE Xingshi, DING Wenjing, YANG Xinshe. Bat algorithm based on simulated annealing and gaussion perturbations[J]. Neural Computing and Applications, 2014, 25(2): 459-468 DOI:10.1007/s00521-013-1518-4 |
| [5] | YILMAZ Selim, KUCUKSILLE Ecir. Improved bat algorithm (IBA) on continuous optimization problems[J]. Lecture Notes on Software Engineering, 2013, 1(3): 279-283 |
| [6] | YANG Xinshe. Bat algorithm for multiobjective optimization[J]. International Journal Bio-Inspired Computation, 2011, 3(5): 267-274 DOI:10.1504/IJBIC.2011.042259 |
| [7] |
李枝勇, 马良, 张惠珍. 蝙蝠算法在多目标多选择背包问题中的应用[J].
计算机仿真, 2013, 30(10): 350-353 LI Zhiyong, MA Liang, ZHANG Huizhen. Application of bat algorithm in multi-objective and multi-choice knapsack problem[J]. Computer Simulation, 2013, 30(10): 350-353 |
| [8] | YANG Xinshe, GANDOMI A H. Bat algorithm:A novel approach for global engineering optimization[J]. Engineering Computations, 2012, 29(5): 464-483 DOI:10.1108/02644401211235834 |
| [9] | MISHRA S, SHAW K, MISHRA D. A new metaheuristic classification approach for microarray data[J]. Procedia Technology, 2012, 4(1): 802-806 |
| [10] | KHAN K, NIKOV A, SAHAI A.A fuzzy bat clusterig method for ergonomic screening of office workplaces, S3T 2011[C]//Advances in Intelligent and Soft Computing, Berlin:Springer, 2011:59-66. |
| [11] | KHAN K, SAHAI A. A comparison of BA, GA, PSO, BP and LM for training feed forward neural networks in e-learning context[J]. International Journal of Intelligent Systems and Applications, 2012, 4(7): 23-29 DOI:10.5815/ijisa |
| [12] |
黄光球, 赵魏娟, 陆秋琴. 求解大规模优化问题的可全局收敛蝙蝠算法[J].
计算机应用研究, 2013, 30(5): 1323-1328 HUANG Guangqiu, ZHAO Weijuan, LU Qiuqin. Bat algorithm with global convergence for solving large-scale optimization problem[J]. Application Research of Computers, 2013, 30(5): 1323-1328 |
| [13] |
李枝勇, 马良, 张慧珍. 蝙蝠算法收敛性分析[J].
数学的实践与认识, 2013, 43(12): 182-190 LI Zhiyong, MA Liang, ZHANG Huizhen. Convergence analysis of bat algorithm[J]. Mathematics in Practice and Theory, 2013, 43(12): 182-190 |
| [14] |
丁文静, 贺兴时, 杨新社, 等. 改进蝙蝠算法在多目标优化中的应用[J].
纺织高校基础科学学报, 2013, 26(4): 538-542 DING Wenjing, HE Xingshi, YANG Xinshe, et al. The application of the improved bats algorithm in multi-objective optimization[J]. Basic Sciences Journal of Textile Universities, 2013, 26(4): 538-542 |
| [15] |
肖辉辉, 段艳明. 改进的蝙蝠算法在数值积分中的应用研究[J].
智能系统学报, 2014, 9(3): 364-371 XIAO Huihui, DUAN Yanming. Application of the improved bat algorithm in numerical integration[J]. CAAL Transactions on Intelligence Systems, 2014, 9(3): 364-371 |
| [16] |
盛晓华, 叶春明. 蝙蝠算法在PFSP调度问题中的应用研究[J].
工业工程, 2013, 16(1): 119-124 SHENG Xiaohua, YE Chunming. Application of bat algorithm to permutation flow-shop scheduling problem[J]. Industrial Engineering Journal, 2013, 16(1): 119-124 |
| [17] |
张勇凯, 李芳, 包晓晓. 改进蝙蝠算法在云制造供应链中的应用[J].
数学理论与应用, 2015, 35(2): 83-94 ZHANG Yongkai, LI Fang, BAO Xiaoxiao. Application of an improved bat algorithm in cloud manufacturing supply chains[J]. Mathmatical Theory and Applications, 2015, 35(2): 83-94 |
| [18] |
于泉, 孙顺远, 徐保国, 等. 基于蝙蝠-拟牛顿混合算法的无线传感器网络节点定位[J].
计算机应用, 2015, 35(5): 1238-1241 YU Quan, SUN Shunyuan, XU Baoguo, et al. Node localization of wireless sensor networks based on hybrid bat-quasi-Newton algorithm[J]. Journal of Computer Applications, 2015, 35(5): 1238-1241 |
| [19] |
周宗渠, 田大钢. 改进蝙蝠算法求解置换流水线车间调度问题[J].
信息技术, 2015, 37(5): 140-143 ZHOU Zongqu, TIAN Dagang. Improved bat algorithm for permutation flow-shop scheduling problem[J]. Information Tecnology, 2015, 37(5): 140-143 |
| [20] |
范彬, 周力行, 黄頔, 等. 基于改进蝙蝠算法的配电网分布式电源规划[J].
电力建设, 2015, 36(3): 123-128 FAN Bin, ZHOU Lixing, HUANG di, et al. Distributed generation planning for distribution network based on modified bat algorithm[J]. Electric Power Construction, 2015, 36(3): 123-128 |



