噪声广泛存在于自然界的各个领域, 包括生物、物理、化学、医学等.传统观念认为噪声会影响信息传递的精确性, 总是消极的.噪声在产生杂乱的运动, 破坏序, 破坏功能, 抹去相与相之间的差别, 导致均匀, 起到了破坏的相变作用,是造成系统无序的根源.所以, 人们想尽各种办法消去噪声对系统的影响.但研究发现, 这种无规律的随机干扰并不总是对系统起到消极破坏的作用,在一定的非线性条件下它在产生相干运动和建立“序”上起到了十分积极的作用.如色关联的色噪声驱动的双稳杜芬模型的稳态分析[1], 噪声可以抑制肿瘤细胞的增长[2]等.通过研究带有噪声的非线性系统, 发现许多确定性方程不可能产生的相变在噪声作用下却成为可能.噪声诱导下非线性动力学系统的相变就是其中的一个重要问题[3].研究发现, 当系统的某个参数达到某一临界值时, 稳态概率密度函数曲线的结构发生变化, 即峰值数目发生变化.文献[4]研究了非高斯色噪声对FHN神经元系统的影响,文献[5]发现噪声在基因转录调控过程中可以诱导蛋白质浓度发生变化,文献[6]研究了乘性噪声和加性噪声之间色关联的单模激光系统的定态性质,文献[7]对色关联白噪声驱动的双稳系统的稳态进行分析,文献[8]研究了带有对称利维噪声的肿瘤免疫系统的随机分岔,文献[9]研究了白噪声驱动下双稳系统的稳态性质,文献[10]研究了色关联作用下单模激光损失模型的光强定态问题,文献[11]研究了色关联的白噪声驱动的双稳系统的随机共振,文献[12]研究了高斯白噪声对神经网络模型随机共振的影响.
上述研究中, 大部分都局限在带有双势阱系统和单势阱系统模型中, 对三势阱系统的分析并不多.文献[13]研究了色关联的三势阱系统下时滞诱导相变,文献[14]研究了色关联乘性和加性色噪声驱动的多稳态系统的稳态特性,文献[15]研究了非高斯噪声激励的三势阱系统的随机响应.本文研究关联乘性和加性的高斯白噪声驱动的多稳系统的稳态特性.分别讨论了关联强度λ, 加性噪声强度Q和乘性噪声强度P对稳态概率密度函数的影响, 研究噪声诱导相变现象的产生.
1 三稳态系统的概率密度函数考虑关联的乘性和加性高斯白噪声共同驱动的三稳系统,由下列的一维朗之万方程来表示:
| $ \frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} = - V'\left( x \right) + x\left( t \right)\xi \left( t \right) + \eta \left( t \right), $ | (1) |
| $ V\left( x \right) = \frac{\alpha }{2}{x^2} - \frac{\beta }{4}{x^4} + \frac{\gamma }{6}{x^6}. $ | (2) |
其中,V(x) 是确定性的势函数,ξ(t) 和η(t) 分别为乘性和加性高斯白噪声,统计性质为
| $ \left\{ \begin{array}{l} \left\langle {\xi \left( t \right)} \right\rangle = \left\langle {\eta \left( t \right)} \right\rangle = 0, \\ \left\langle {\xi \left( t \right)\xi \left( {t'} \right)} \right\rangle = 2P\delta \left( {t - t'} \right), \\ \left\langle {\eta \left( t \right)\eta \left( {t'} \right)} \right\rangle = 2Q\delta \left( {t - t'} \right), \\ \left\langle {\xi \left( t \right)\eta \left( {t'} \right)} \right\rangle = \left\langle {\xi \left( {t'} \right)\eta \left( t \right)} \right\rangle = 2\lambda \sqrt {PQ} \delta \left( {t - t'} \right). \end{array} \right. $ | (3) |
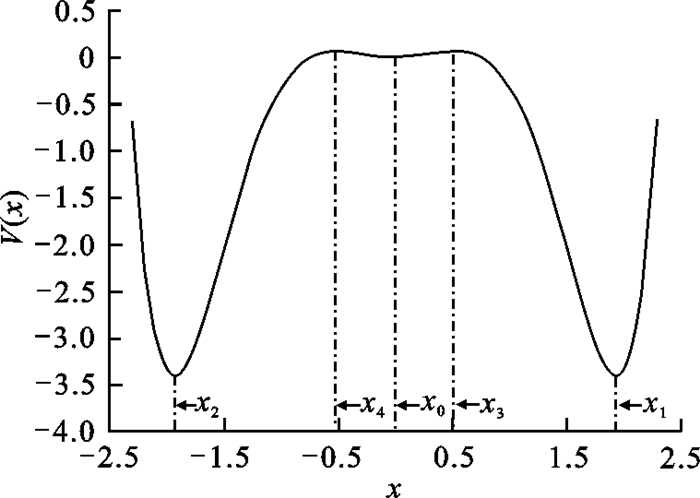
参数P和Q分别是乘性和加性高斯白噪声的强度,参数λ表示乘性与加性高斯白噪声的关联强度,且满足|λ| < 1.确定性势函数V(x) 在α < 0, β>0和γ>0和β2+4αγ>0条件下表示一个对称三稳势函数,它具有三个稳定点x0, x1, x2和两个不稳态点x3, x4分别为
|
| 图 1 确定性势函数V(x) 关于x的曲线(α=-1, β=4, γ=1) Fig.1 The curve of the deterministic potential V(x) on x(α=-1, β=4, γ=1) |
利用刘维方程[16]和诺维科夫定理[17],从方程(1)~(3) 得到近似的福克-普朗克方程为
| $ \begin{array}{*{20}{c}} {\frac{{\partial \rho \left( {x, t} \right)}}{{\partial t}} = - \frac{\partial }{{\partial x}}\left[{A\left( x \right)\rho \left( {x, t} \right)} \right] + \frac{{{\partial ^2}}}{{\partial {x^2}}}\left[{B\left( x \right)\rho \left( {x, t} \right)} \right], }\\ {A\left( x \right) = \alpha x + \beta {x^3} - \gamma {x^5} + \left( {1/2} \right)B{{\left( x \right)}^\prime }, B\left( x \right) = P{x^2} + 2\lambda \sqrt {PQ} + Q.} \end{array} $ | (4) |
方程(4) 对应的稳态概率密度函数为
| $ {\rho _{st}}\left( x \right) = \frac{N}{{\sqrt {B\left( x \right)} }}\exp \left[{-\frac{{\mathit{\Phi }\left( x \right)}}{P}} \right]. $ | (5) |
式(5) 中N为归一化常数, 广义势函数Φ(x) 的表达式为
| $ \mathit{\Phi }\left( x \right) = {A_1}{x^4}/4 + {A_2}{x^3}/3 + {A_3}{x^2}/2 + {A_4}x + {A_5}. $ | (6) |
其中
| $ \begin{align} & R=Q/P,F=\lambda \sqrt{R},G=\sqrt{{{F}^{2}}-R},{{A}_{1}}=\gamma ,{{A}_{2}}=-2F{{A}_{1}},{{A}_{3}}=\left( 4{{F}^{2}}-R \right){{A}_{1}}-\beta ,{{A}_{4}}= \\ & 2F\left( R{{A}_{1}}+ \right.\left. A\left( \alpha =-1,\beta =4,\gamma =1 \right)3 \right),{{A}_{5}}={{A}_{6}}\ln B\left( x \right)+H\left( x \right),{{A}_{6}}= \\ & \frac{1}{2}\left( {{A}_{4}}-\alpha \right),{{A}_{7}}=R\left( R{{A}_{1}}+4{{\lambda }^{2}}{{A}_{3}}+\beta \right),{{A}_{8}}={{A}_{1}}{{R}^{2}}\left( 16{{\lambda }^{4}}-20{{\lambda }^{2}}+5 \right),{{A}_{9}}= \\ & \left( -4{{F}^{2}}+3R \right)\beta -\alpha ,{{A}_{10}}=\frac{F\left( {{A}_{8}}+{{A}_{9}} \right)}{G},C\left( x \right)=x+F,B\left( x \right)={{x}^{2}}+2FX \\ & +R,H\left( x \right)={{A}_{10}}\tanh \frac{C\left( x \right)}{G}. \\ \end{align} $ |
通过数值计算方程(5), 讨论关联强度λ, 加性噪声强度Q和乘性噪声强度P对稳态概率密度函数的影响.这里取α=-1, β=4, γ=1, 以下结论均在这组参数下讨论得出.
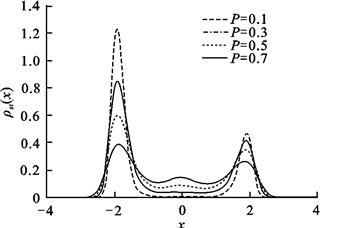
图 2为关联强度λ取不同值时, 稳态概率密度函数ρst(x) 关于x的函数图像.当参数P=0.5, Q=0.5时, 可以看出, 随着λ的增大, 稳态概率密度函数由三峰结构变为单峰结构, 即λ可以诱导相变现象产生.在出现三峰的情况下, 左峰比右峰高, 随着λ的增强, 稳态概率密度函数由三峰结构变为双峰结构.伴随着λ的进一步增大, 左边的增到最大, 右峰完全消失, 变成了单峰结构.

|
| 图 2 稳态概率密度函数在不同关联强度下的变化曲线 Fig.2 Plot of the stationary probability distribution function for different cross-correlation intensities |
图 3为稳态概率密度函数ρst(x) 在不同加性噪声强度Q下的变化曲线.当参数P=0.5, λ=0.1时, 可以看出, 随着Q增加, 稳态概率密度函数的左右峰均下降, 中峰上升, 但还保留着三峰结构.表明随着Q的增加, 稳态概率密度函数峰的个数没有发生变化, 即Q不可以诱导相变现象的产生.

|
| 图 3 稳态概率密度函数在不同加性噪声强度Q下的变化曲线 Fig.3 Polt of the stationary probability distribution function for different additive noise intensities |
图 4给出了稳态概率密度函数ρst(x) 作为x的函数,乘性噪声强度P取不同值.当参数Q=0.5, λ=0.1时,可以看出,随着P的增大,稳态概率密度函有选举权的左峰比右峰下降的速度更快,而中峰却慢慢上升,峰的结构由双峰变成了三峰.表明随着P的增加,稳态概率密度函数峰的结构发生了变化,即P可以诱导相变现象产生.
|
| 图 4 稳态概率密度函数在不同乘性图噪声强度下的变化曲线 Fig.4 Plot of the stationary probability distibution function for different multiplicative noise intensities |
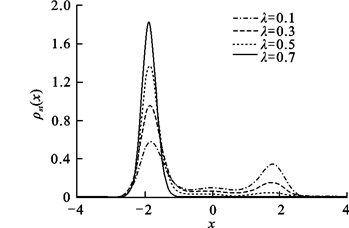
为了进一步验证白噪声作用下三稳系统的稳态概率密度函数,对其进行模拟.这里对方程(1) 采取向前Eular算法,利用Box-Muller算法[18]产生高斯白噪声.结果如图 5~77所示.可以看到白噪声参数对稳态概率密度函数的影响和理论结果是一致的.
|
| 图 5 稳态概率密度函数在不同关联强度下的数值模拟图 Fig.5 Simulation results for the stationary probability distribution function with different cross-corretation intensities |
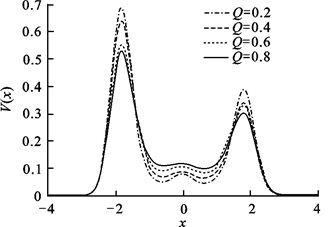
|
| 图 6 稳态概率密度函数在不同加性噪声强度下的数值模拟图 Fig.6 Simulation results for the stationary probability distribution function with different additive noise intensities |

|
| 图 7 稳态概率密度函数在不同乘性噪声强度下的数值模拟图 Fig.7 Simulation results for the stationary probability distribution function with different multiplicative noise intensities |
本文利用理论近似和数值模拟研究了乘性和加性高斯白噪声共同激励下的一维三稳系统的动力学性质.发现关联强度λ, 加性噪声强度Q和乘性噪声强度P对概率密度函数有较大的影响, 并得出以下结论:
(1) 关联强度λ的增加能引起稳态概率函数峰结构的变化, 使得从三峰结构转变为单峰, 从而峰数发生了变化, 即λ能够引起相变;
(2) 加性噪声强度Q的改变使得稳态概率密度函数的左峰和右峰下降, 中峰上升, 峰的结构却没有发生变化, 还保持着三峰结构, 即Q不能诱导相变的产生;
(3) 乘性噪声强度P的增大能够引起稳态概率密度函数从双峰结构向三峰结构变化, 左峰和右峰下降, 中峰上升, 峰数发生变化, 即P能够引起相变的发生.
| [1] | JIN Yanfei, XU Wei, LI Wei, et al. Steady-state analysis of a bistable duffing model driven by additive and multiplicative colored noises with a colored correlated noise[J]. Jouranl of Dynamics and Control, 2005, 3(2): 60-65 |
| [2] | WANG Canjun, QUN Wei, MEI Dongcheng. Assoicated relaxation time and the correlation function for a tumor cell growth system subjected to color noises[J]. Physical Letters A, 2008, 372(13): 2176-2182 DOI:10.1016/j.physleta.2007.11.040 |
| [3] |
胡岗.
随机力与非线性系统[M]. 上海: 上海科技教育出版社, 1994.
HU Gang. Stochastic forces and nonlinear systems[M]. Shanghai: Shanghai Scientific and Technological Education Publishing House, 1994. |
| [4] | ZHAO Yan, XU Wei, ZOU Shaocun. The steady state probability distribution and mean first passage time of FHN neural system driven by non-Gaussian noise[J]. Acta Physica Sinica, 2009, 58(3): 1396-1402 |
| [5] | WANG Canjun. Colored noise induced switch in the gene transcriptional regulatory system[J]. Acta Physica Sinica, 2012, 61(1): 010503 |
| [6] | WU Dan, LUO Xiaoqin, ZHU Shiqun. Flutuations of single-mode laser driven by two different kinds of colored noise[J]. Communications in Theoretical Physics, 2006, 45(4): 630-636 DOI:10.1088/0253-6102/45/4/013 |
| [7] | JIA Ya, LI Jiarong. Stead-state analysis of a bistable system with addibive and multiplicative noises[J]. Physical Review Letters, 1996, 53(6): 5786-5792 |
| [8] | XU Yong, FENG Jing, LI Juanjuan, et al. Stochastic bifurcation for tumor-immune system with symmetric Levy noise[J]. Physical Letters A, 2013, 392(20): 4739-4748 |
| [9] | WU Dajin, CAO Li, KE Shengzhi. Bistable kinetic model driven by correlated noises:Steady-state analysis[J]. Physical Review Letters, 1994, 50(4): 2496-2502 |
| [10] | CHEN Jun, CAO Li, WU Dajin. Bistable kinetic model driven by correlation noises:Unified colored-noise approxiamtion[J]. Physical Review Letters, 1995, 52(3): 3228-3231 |
| [11] | JIN Yanfei, XU Wei, LI Wei, et al. Stochastic resonance in an asymmetric bistable system driven by multiplicative and additive noise[J]. Physics Reports B, 2005, 14(6): 1077-1081 |
| [12] |
胡丽萍, 李鑫. 高斯白噪声对神经元映射模型随机共振的影响[J].
纺织高校基础科学学报, 2014, 27(4): 492-495 HU Liping, LI Xin. Impact of Gaussian white noise on stochastic resonance of map-based neural model[J]. Basic Sciences Journal of Textile Universities, 2014, 27(4): 492-495 |
| [13] | JIA Zhenglin. Time-delay induced reentrance phenomenon in a triple-well potential system driven by cross-corrslated noises[J]. International Journal of Theoretical Physics, 2009, 48(1): 226-231 DOI:10.1007/s10773-008-9797-8 |
| [14] | SHI Peiming, LI Pei, HAN Dongying. Steady-state analysis of a tristable system driven by a correlated multiplicative and and additive colored noises[J]. Acta Physica Sinica, 2014, 63(17): 170504 |
| [15] | ZHANG Huiqing, YANG Tingting, XU Wei. Effects of non-Gaussian noise on logical stochastic resonance in a triple-well potential system[J]. Nonlinear Dynamics, 2014, 76(1): 649-656 DOI:10.1007/s11071-013-1158-3 |
| [16] | BENZI R, SUTERA A, VULPINAI A. The mechanism of stochastic resonance[J]. Journal of Physics A:Mathematical and Geneal, 1981, 14(11): L453-L457 DOI:10.1088/0305-4470/14/11/006 |
| [17] | LIANG Guiyun, CAO Lin, WU Dajin. Approximate Fokker-Planck equation of system driven by multiplicative colored noises with colored cross-correlation[J]. Physical Letters A, 2004, 335(3/4): 371-384 |
| [18] | KNUTH D E. The art of computer programming Vol.2[M]. MA: Addiso-Wesley, Reading, 1969. |



