0 引言

我国证券投资基金近年来发展迅速.目前我国基金数目达到2 525支, 基金资产净值达43 495亿元.2001年我国第一只开放式基金发行至今, 开放式基金已经超越了封闭式基金, 成为我国证券基金业的市场主流^[1-3].

在基金理论的发展与基金产业的评价方面, 基金净值是最基础与最关键的因素, 因此研究基金净值的预测很有意义.分析已有的研究成果发现影响基金净值的因素涉及方面较多^[4-21], 传统预测方法不能反映基金净值与政治、经济等多种因素之间的非线性规律, 对基金净值预测偏离较大, 因此人们开始寻找其他方法解决这些问题.考虑到BP神经网络的自适应性可以较好地解决上述问题, 王波^[22]将BP神经网络理论引入基金周净值预测模型中, 结果表明, 该模型能够准确预测基金周净值的短期走向和周净值曲线变化的拐点.在预测基金日净值方面, 刘丽峰^[23]证实了粒子群优化与BP神经网络模型可以提高基金净值预测的精度, 有效解决了传统预测方法不能反映基金净值与政治、经济等多种因素之间的非线性规律而导致的预测精度低的问题.上述方法对基金净值预测的精度有所提高, 但建立模型时均需要选取基金净值的影响指标, 指标选取的合适与否决定模型预测精度的高低, 并且涉及的指标越多, 数据收集与处理的工作量越大.乔宝明^[24]等采用小波去噪原理对基金净值序列进行消噪处理, 使得到的新序列具有更好的平稳性, 然后对新序列建立AR模型, 实证发现小波去噪能够显著提高AR模型的预测精度.李小康^[25]运用极大值分布GPD模型对基金净值样本数据的极值点进行了较为理想的预测.上述基金净值的预测精度虽然有所提高, 但小波去噪的同时也会滤去数据中有效的信息从而导致预测值的绝对百分比误差仍较高.

为了更好地预测证券投资基金的净值, 避免小波去噪可能导致数据中有效信息流失的问题, 本文根据小波分解原理, 结合传统的ARMA-GARCH模型建立了小波分解ARMA-GARCH模型.将基金净值序列分解到不同的层(即不同尺度) 得到趋势序列与不同层对应的细节序列, 对得到的新序列分别建立ARMA-GARCH模型, 重组各个ARMA-GARCH模型的预测值后得到基金净值的预测值, 尽可能地保留数据原有的信息, 从而进一步提高预测精度, 降低误差.

1 预备知识 1.1 ARMA模型

自回归平均移动模型(ARMA) 描述序列{x_t}在t时刻的取值受到前p个时刻自身取值与前q个时刻的残差项{ε_t}的线性影响, 表示为ARMA (p, q) 模型${x_t} = c + \sum\limits_{i = 1}^p {{\alpha _{t - i}}{x_{t - i}} + {\varepsilon _t}} + \sum\limits_{i = 1}^q {{\beta _{t - i}}{\varepsilon _{t - i}}} $.如果q=0, 得到p阶自回归模型AR (p), 如果p=0, 得到q阶移动平均模型MA (q).

1.2 GARCH模型

Engle^[26]提出自回归条件异方差模型(ARCH) 来刻画数据波动的时变特征, 即在以往信息I_t-1已知的条件下对方差σ_t²建模.ARCH模型由均值方程${y_t} = c + \beta {x_t} + {\varepsilon _t}, {\varepsilon _t}|{I_{t - 1}}~N\left( {0, \sigma _t^2} \right)$与条件方差方程σ_t²=$w + \sum\limits_{i = 1}^q {{\alpha _i}\varepsilon _{t - i}^2} $构成, 其中c与w为常数, ε_t为均值方程的残差项.

为克服实际分析时ARCH模型阶数q较大导致计算效率低的情况, Bollerslev^[27]提出了广义自回归条件异方差模型(GARCH).GARCH (p, q) 模型是对ARCH (q) 模型的拓展, 其条件方差方程$\sigma _i^2 = w + \sum\limits_{i = 1}^q {{\alpha _i}\varepsilon _{t - i}^2} + \sum\limits_{i = 1}^p {{\beta _i}\sigma _{t - i}^2} $考虑了以往期方差对当期预测方差的影响, 从而降低ARCH模型的阶数, 更好地反应方差的时变特征.

1.3 小波分析

小波分析是将信号或函数用一个基小波函数的平移与伸缩变换进行细化表示或者逼近.基小波φ(t) 具有瞬时衰减震荡特征且满足容许性条件${C_\varphi } = \int_{\text{R}} {\frac{{{{\left| {\hat \varphi \left( w \right)} \right|}^2}}}{w}} {\text{d}}w < + \infty \left( {\hat \varphi \left( w \right){\text{是}}\varphi \left( t \right)的傅立叶变换} \right)$, 经平移b、伸缩a(≠0) 变换得到小波基$\left\{ {\varphi \left( {\frac{{t - b}}{a}} \right)} \right\}$.函数x(t) 在L²(R) 上的小波变换为

$ {W_\varphi }\left( {b,a} \right) = {\left| a \right|^{ - 1/2}}\int_{\bf{R}} {x\left( t \right)\overline {\varphi \left( {\frac{{t - b}}{a}} \right)} {\rm{d}}t,x \in {L^2}\left( {\bf{R}} \right),a,b \in {\bf{R}}} \;aaa\;a \ne 0, $

(1)

重构函数为

$ x\left( t \right) = \frac{1}{{{C_\varphi }}}\int_{\bf{R}} {\int_{\bf{R}} {{W_\varphi }\left( {b,a} \right){a^{ - 1/2}}\varphi \left( {\frac{{t - b}}{a}} \right)\frac{{{\rm{d}}a{\rm{d}}b}}{{{a^2}}}} } . $

(2)

取a=2^j, b=k2^j, 将连续小波${\varphi \left( {\frac{{t - b}}{a}} \right)}$离散化后得离散二进小波^[28-29], 记为φ_{j, k}(t)=2^-j/2φ(2^-jt-k), 代入式(1) 与式(2) 可得离散小波积分的小波变换

$ DW{T_\varphi }\left( {j,k} \right) = {2^{ - j/2}}\int_{\bf{R}} {x\left( t \right)\bar \varphi \left( {{2^{ - j}}t - k} \right){\rm{d}}t} , $

(3)

二进离散小波变换重构函数为

$ x\left( t \right) = \sum\limits_{j,k \in Z} {DW{T_\varphi }\left( {j,k} \right){\varphi _{j,k}}\left( t \right)} . $

(4)

1.4 多分辨率分析

多分辨率分析(MRA) 是S. Mallat和Y. Meyer于1986年在多尺度逼近的基础上提出的一个理解和构造小波的统一框架的概念^[30].

设V_j=span{2^-j/2φ(2^-jt-k)}(j∈Z) 是L²(R) 上的一个具有嵌套性、逼近性、伸缩性和平移不变性的空间序列, 那么V_j(j∈Z) 为L²(R) 的多分辨率分析.根据多分辨率理论, 空间V_j可以分解为V_j=W_j-1⊕V_j-1=W_j-1⊕W_j-2⊕V_j-2=…=W_j-1⊕W_j-2⊕…⊕W_j-m⊕V_j-m, 其中W_j=span{2^-j/2φ(2^-jt-k)}(j∈Z), 子空间W_j-1, W_j-2, …, W_j-m, V_j-m相互正交.那么, L²(R)=⊕W_j, 则x(t)∈L²(R) 可以表示为

$ x\left( t \right) = \sum\limits_k {{c_{0,k}}{\phi _{0,k}}\left( t \right)} + \sum\limits_{j = 0}^\infty {\sum\limits_k {{d_{j,k}}{\varphi _{j,k}}\left( t \right)} } . $

(5)

其中, φ是具有低频性质的尺度函数, φ是具有高频性质的小波函数, c_{0, k}=〈x, φ_{0, k}〉, d_{j, k}=〈x, φ_{j, k}〉.式(5) 的前一项为刻画信号f(t) 的低频信息的趋势项, 记为A_{0, t}, 后一项为刻画高频信息的细节项, 记为∑$\sum\limits_{l = 1}^\infty {{D_{l, t}}} $, 则式(5) 可以表示为

$ {x_t} = {A_{0,t}} + \sum\limits_{l = 1}^\infty {{D_{l,t}}} . $

(6)

如引言所述, 经典的ARMA-GARCH模型预测精度有待进一步提高, 而小波分解可以刻画信号的细节部分, 提高时间序列数据的利用率, 将小波分解原理与经典的ARMA-GARCH模型相结合可以提高模型的预测精度, 因此本文将构建一种基于小波分解的小波ARMA-GARCH模型.

2 小波分解ARMA-GARCH模型

小波分解ARMA-GARCH模型的基本思想是:根据小波理论将离散时间序列{S_t}进行L分解后得到1个趋势系数序列和L个细节系数序列, 对系数序列单支重构后得到趋势序列{A_{L, t}}与细节序列{D_{l, t}}, l=1, 2, …, L.由式(6) 得

$ {S_t} = {A_{L,t}} + \sum\limits_{l = 1}^L {{D_{l,t}}} . $

(7)

对趋势序列和细节序列分别建立ARMA模型, 对存在ARCH效应的模型建立GARCH模型, 采用静态预测方法对未来数据进行预测, 根据式(7) 重组各层预测数据, 获得序列{S_t}的预测值${\hat S_t}$.

Daubechies小波具有紧支撑、正交、非对称的性质, 其消失矩选取对小波函数的光滑度与支撑度以及小波变换的计算量都有影响, 而消失矩为4的Daubechies小波db4在满足光滑度的同时支撑度最小, 因此本文选取db4(L) 小波.

趋势序列的ARMA模型的可决系数随小波分解层数的增加而越大, 可决系数越大, 模型的拟合效果越好, 预测误差越小; 另一方面, 分解层数的增加不仅使得趋势序列与原序列的标准离差变大, 还使得建立的细节序列ARMA模型增加, 二者均导致预测误差增大.综合考虑以上因素, 本文在可决系数一定的情况下趋势序列的最低层次为小波分解层数.另外, 为减少模型选取带来的工作量, ARMA的p和q阶数均小于6.

模型预测结果评价标准采用绝对百分比误差APE和平均绝对百分比误差MAPE.二者计算公式分别为${\text{AP}}{{\text{E}}_t} = 100\left| {\left( {{{\hat S}_t} - {S_t}} \right)/{S_t}} \right|, MAP{E_t} = {\left( {T + 1} \right)^{ - 1}}\sum\limits_{t = 1}^T {{\text{AP}}{{\text{E}}_t}} $.APE衡量的是单日预测值偏离实际值的百分比, MAPE衡量的是连续T日的预测值偏离实际值的百分比.APE与MAPE的值越小, 则预测精度越高, 模型实用性越好.

3 实证分析

从中国基金网获取天弘周期策略股票型基金(420005)2010年1月4日至2015年8月26日共1 369个累计净值数据.以前1 169个数据{S_t}为样本数据进行小波分解ARMA-GARCH建模, 后200个数据留作模型预测评价参考数据.

将样本期基金累计净值{S_t}小波分解重构的各层趋势序列建立ARMA (p, q) 模型.由表 1可知, 可决系数R²达到0.99的最低分解层数为5, 因此小波分解5层.

对累计净值序列进行db4(5) 分解并单支重构的趋势序列与各层细节序列, 见图 1.图 1中, S为累计净值序列, A₅为趋势序列, D₁~D₅分别为1~5层细节序列.A₅与S相比, 两条曲线的趋势大致相似, 但A₅更平滑, 使得累计净值频繁波动的信息分散存储于各层细节序列.

检验趋势序列与细节序列的平稳性, DAF单位根检验结果见表 2.表 2显示, 细节序列均为平稳序列, 趋势序列A₅不平稳, 但A₅的一次差分序列DA₅是平稳的.

对各平稳序列建立合适的ARMA模型, 检验是否存在ARCH效应, 并对存在ARCH效应的模型建立合适的GARCH模型(见表 3), 各序列模型如下:

$ \begin{array}{l} \left\{ \begin{array}{l} {D_{1,t}} = 1.6120{D_{1,t - 1}} - 0.8663{D_{1,t - 2}} + \\ \;\;\;\;\;0.3983{\mu _{t - 1}} - 0.5721{\mu _{t - 2}} + 0.0530{\mu _{t - 3}} - 0.9768{\mu _{t - 4}} - 0.4501{\mu _{t - 5}} + 0.5555{\mu _{t - 6}},\\ \sigma _t^2 = 0.2973\varepsilon _{t - 1}^2, \end{array} \right.\\ \left\{ \begin{array}{l} {D_{2,t}} = 0.3626{D_{2,t - 1}} - 0.3125{D_{2,t - 2}} + \\ \;\;\;\;\;1.1750{\mu _{t - 1}} - 0.9570{\mu _{t - 2}} + 1.5374{\mu _{t - 3}} - 0.3224{\mu _{t - 5}},\\ \sigma _t^2 = 0.6218\varepsilon _{t - 1}^2, \end{array} \right.\\ {D_{3,t}} = - 0.7446{D_{3,t - 1}} - 0.4796{D_{3,t - 2}} - 0.5050{D_{3,t - 3}} - 0.0868{D_{3,t - 4}} - \\ \;\;\;\;\;\;\;\;1.8281{\mu _{t - 1}} + 0.0803{\mu _{t - 2}} + 1.3543{\mu _{t - 3}} - 0.6062{\mu _{t - 4}},\\ \left\{ \begin{array}{l} {D_{4,t}} = 1.1351{D_{4,t - 1}} + 0.2576{D_{4,t - 2}} - 0.4275{D_{4,t - 3}} - 0.1141{D_{4,t - 4}} + \\ \;\;\;\;\;\;1.1972{\mu _{t - 1}} - 0.0175{\mu _{t - 5}} + 0.1815{\mu _{t - 6}},\\ \sigma _t^2 = 0.6307\varepsilon _{t - 1}^2, \end{array} \right.\\ \left\{ \begin{array}{l} {D_{5,t}} = 1.6013{D_{5,t - 1}} - 0.3815{D_{5,t - 2}} - 0.1707{D_{5,t - 3}} - 0.0777{D_{5,t - 4}} + \\ \;\;\;\;\;\;1.2835{\mu _{t - 1}} + 0.5829{\mu _{t - 2}} - 0.4014{\mu _{t - 4}} - 0.6938{\mu _{t - 5}}, \end{array} \right.\\ D{A_{5,t}} = 0.5084D{A_{5,t - 1}} + 0.3609D{A_{5,t - 2}} + 0.8944D{A_{5,t - 3}} - 0.4314D{A_{5,t - 4}} - 0.1118D{A_{5,t - 5}} - \\ \;\;\;\;\;\;\;\;\;\;\;0.2365D{A_{5,t - 6}} + 1.2354{\mu _{t - 1}} + 0.9525{\mu _{t - 2}} - 0.7672{\mu _{t - 4}} - 1.1192{\mu _{t - 5}} - 0.7244{\mu _{t - 6}}. \end{array} $

根据表 3, DA₅、D₃与D₅的F统计量的伴随概率分别为0.073 2, 0.124 6和0.483 9;D₁, D₂与D₄伴随概率均为0, 那么, 在95%的置信水平下D₁, D₂与D₄存在ARCH效应, 需建立GARCH模型.表 3说明小波分解将累计净值具有的集聚特征分散到了细节序列.

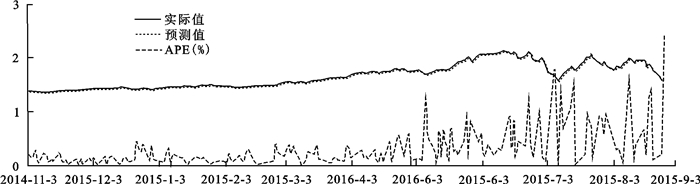
依据各序列模型分别进行静态估计, 预测未来200个工作日的数据, 并根据式(7) 得到天宏周期策略基金的预测累计净值, 其与实际值的对比情况见图 2, 单日预测1日至10日10个APE值与连续预测的20日至200日等分的10个预测期的MAPE值见表 4.

表 4中的模型1是指本文模型即小波分解ARMA-GARCH模型, 模型2是指小波去噪AR模型, 模型3是指传统的ARMA-GARCH模型.1日至10日的APE结果显示, 小波分解ARMA-GARCH模型对第4日的预测效果最好, APE值为0.019 0%, 其余日的APE波动相对较大, 介于0.021 4%~0.284 0%之间, 因此, 单日净值预测精度较好.MAPE值则随着预测期的增加而变大, 意味着模型对连续预测的预测精度随着预测期T的缩短而提高.对比3个模型预测精度, 小波分解ARMA-GARCH模型的APE、MAPE值都普遍低于小波去噪AR模型与ARMA-GARCH模型的对应值, 这说明前者预测精度显著优于后两者.

由图 2可直观看出, 小波分解ARMA-GARCH模型的预测值与实际值两条曲线大致重合, APE始终低于2.5%, 模型的单日预测精度较高.在实际值曲线的峰顶和谷底处, APE曲线快速攀至峰值, 预测曲线与实际曲线的重合程度较低, 预测效果变差.2015年5月前APE较小, 之后的APE仍存在取值较小的区域但普遍取值高于之前的水平, 结合实际值曲线在预测期的前期走势平缓, 从2015年5月之后波动幅度明显变大的情况, 可以推知模型的单日预测精度在平缓期显著优于震荡期.

小波去噪AR模型同小波分解ARMA-GARCH模型都是将小波分析理论引入到自回归模型中, 不同之处有4点.首先在计量模型的选取方面, 前者采用了AR模型, 后者则考虑到基金预测模型中存在的ARCH效应而使用GARCH模型进行修正; 其次, 两个模型使用的小波分析理论的方法不同, 前者使用了小波分析理论的去噪方法对原序列进行去噪, 使新序列具有更好的稳定性, 后者使用了小波分析理论的分解方法, 将原序列分解到不同尺度上, 从而得到趋势序列与各尺度的细节序列, 对各序列分别建立ARMA-GARCH模型; 再次, 从研究期而言, 前者的研究期不到五个月, 而后者研究期跨度显著大于前者, 因而后者更加真实、准确地反映了基金净值的曲线趋势; 最后, 二者的预测效果不同, 实证结果表明小波分解ARMA-GARCH模型预测精度更高.

4 结束语

本文建立了小波分解ARMA-GARCH模型, 利用天宏周期策略股票型基金的累计净值数据进行了实证分析与预测, 并将预测结果与小波去噪AR模型预测结果、ARMA-GARCH模型预测结果进行了比较.实证分析结果表明, 本文模型的单日预测精度较高且预测效果在平稳期显著优于震荡期, 在基金净值实际值曲线的峰顶和谷底处的预测效果略差, 连续预测的精度则随着预测期的增加而降低.最后与小波去噪AR模型的预测效果和ARMA-GARCH模型的预测效果相比, 本文模型的预测精度更高, 因此本文模型对于基金净值预测方面具有实用价值.